
- •2. Приведение произвольной системы сил к простейшему виду. Условия равновесия произвольной системы сил
- •3. Растяжение и сжатие стержня. Продольная сила. Условия прочности при растяжении
- •1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Метод Крамера и Гаусса.
- •2. Модель идеального совершенного газа. Интеграл Бернулли для адиабатических течений совершенного газа. Сопло Лаваля
- •3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •1. Векторные пространства. Линейная зависимость векторов. Базис. Размерность
- •3. Движение твердого тела вокруг одной неподвижной точки. Скорости и ускорения точек тела
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •3. Кручение стержня круглого поперечного сечения. Крутящий момент. Условия прочности и жесткости при кручении.
- •1. Линейные операторы и их матрицы. Собственные значения и собственные векторы. Нормальные формы матрицы линейного оператора
- •1. Кривые второго порядка. Их канонические уравнения
- •2. Сложное движение точки. Теоремы о сложении скоростей и ускорений
- •3. Изгиб балки. Нормальные и касательные напряжения. Условие прочности
- •Касательные напряжения в продольных сечениях балки
- •Проверка прочности и подбор сечения балки
- •1. Поверхности второго порядка. Их канонические уравнения
- •2. Уравнения Лагранжа 2-ого рода
- •3. Модель идеальной жидкости. Интегралы уравнений движения идеальной жидкости
- •2. Общие теоремы динамики точки
- •1. Элементы теории поля. Поток, дивергенция, ротор вектора. Теорема Гаусса-Остроградского. Теорема Стокса
- •2. Прямолинейные колебания материальной точки
- •2. Движение точки в поле центральных сил. Формулы Бине
- •2. Движение планет. Закон всемирного тяготения.
- •3. Энергетические методы определения перемещений. Теорема Кастилиано. Интеграл Мора. Правило Верещагина.
- •1. Формула Тейлора и ее остаточный член
- •2. Определение траектории материальной точки в ньютоновом поле тяготения. Искусственные спутники Земли
- •3. Гравитационные волны в идеальной жидкости
- •1. Ряды Фурье. Основные свойства коэффициентов Фурье. Неравенство Бесселя
- •2. Движение несвободной материальной точки. Плоский математический маятник.
- •3. Канонические уравнения метода сил при изгибе балок и рам
- •1. Теорема Вейерштрасса о равномерной сходимости функционального ряда.
- •2. Динамика относительного движения материальной точки. Относительный покой и относительное движение вблизи поверхности Земли.
- •2. Общие теоремы динамики системы
- •3. Устойчивость упругих стержней. Критическая сила
- •1. Степенные ряды и их свойства. Интервал и радиус сходимости
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задача Циолковского
- •3. Слоистые течения. Течение Пуазейля, течение Куэтта, течение под действием силы тяжести
- •2. Принцип возможных перемещений
- •3. Постановка задач теории упругости в компонентах перемещений и напряжений
- •1. Достаточные условия сходимости ряда Фурье
- •2. Поверхности разрыва внутри идеальных сжимаемых сред. Адиабата Гюгонио
- •3. Плоскопараллельное движение твердого тела. Определение скоростей и ускорений точек тела
- •1. Определение интеграла Римана и достаточные условия его существования
- •2. Уравнения Лагранжа 2-ого рода
- •3. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
- •2. Канонические уравнения движения системы
- •3. Основы теории пограничного слоя. Уравнения Прандтля
- •1. Элементы теории поля. Поток, дивергенция, ротор в-ра. Т-ма Гаусса-Остроградского. Т-ма Стокса
- •2. Вращение абсолютно твердого тела вокруг неподвижной оси. Давление на ось
- •3. Уравнения Ламе движения упругого тела в перемещениях
- •1. Элементы теории поля. Поток, дивергенция, ротор в-ра. Т-ма Гаусса-Остроградского. Т-ма Стокса
- •2. Движение абсолютно твердого тела, имеющего одну неподвижную точку. Кинематические уравнения Эйлера
- •3. Основы теории пограничного слоя
- •1. Группа,поле, кольцо
- •2. Динамические уравнения Эйлера
- •3. Представление решений уравнений Ламе в форме Папковича-Нейбера
- •1. Определение и примеры конформных отображений
- •2. Первые интегралы. Проблема 4-го интеграла. Элементарная теория гироскопа
- •3. Модель идеальной жидкости и газа. Интегралы уравнений движения идеальной жидкости. Сопло Лаваля
- •1. Интегральная теорема Коши
- •Доказательство
- •2. Элементарная теория гироскопов. Движение тяжелого твердого тела вокруг неподвижной точки
- •3. Кручение призматических стержней произвольного постоянного поперечного сечения
- •1. Теорема о разложении аналитической функции в ряд Тейлора
- •2. Принцип Остроградского-Гамильтона
- •3. Модель идеального совершенного газа. Интеграл Бернулли для адиабатических течений совершенного газа. Сопло Лаваля
- •1. Теорема о представимости функции рядом Лорана
- •2. Действие удара на тело, вращающееся вокруг неподвижной оси. Центр удара
- •3. Уравнения Ламе движения упругого тела в перемещениях
- •3. Кручение стержня круглого поперечного сечения. Крутящий момент. Условия прочности и жесткости при кручении.
- •1. Изолированные особые точки аналитических функций и их классификация
- •2. Общие теоремы динамики системы
- •3. Изгиб балки. Нормальные и касательные напряжения. Условие прочности
- •Касательные напряжения в продольных сечениях балки
- •Проверка прочности и подбор сечения балки
- •1. Линейное уравнение n-го порядка с постоянными коэффициентами
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задачи Циолковского
- •3. Слоистые течения. Течение Пуазейля, течение Куэтта, течение под действием силы тяжести
- •1. Линейные неоднородные ду n-го порядка. Метод вариации произвольных постоянных
- •2. Теория удара системы материальных точек. Действие удара на тело, вращающееся вокруг неподвижной оси
- •3. Устойчивость упругих стержней. Критическая сила
- •2. Постановка задач теории упругости в компонентах перемещений и напряжений
- •1. Решение смешанной задачи для уравнения колебаний струны методом Фурье
- •2. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
- •3. Движение несвободной материальной точки. Плоский математический маятник
- •1. Решение смешанных задач для уравнения теплопроводности методом Фурье
- •2. Динамика относительного движения материальной точки
- •3. Одномерные нестационарные течения газа и их характеристики
- •1. Классическая вероятность. Теоремы сложения и умножения. Формула полной вероятности. Биномиальное, нормальное и пуассоновское распределения
- •2. Движение твердого тела около неподвижной точки. Скорости и ускорения точек тела
- •3. Представление решений уравнений Ламе в форме Папковича-Нейбера
- •2. Движение абсолютно твердого тела, имеющего одну неподвижную точку. Кинематические уравнения Эйлера
- •3. Базовые принципы мкэ в механике деформируемого твёрдого тела
- •1. Кривизна и кручение. Формулы Френе
- •3. Основные понятия и определения мкэ. Определение и свойства матриц жёсткости, упругости, функций формы, градиентов
- •1. Классификация линейных уравнений в частных производных 2-ого порядка. Примеры уравнений основных типов
- •2. Способы генерации конечно-элементных моделей
- •3. Задача о сильном взрыве в газе
- •1. Случайные величины и их полные характеристики. Характеристическая функция случайной величины и ее свойства. Закон больших чисел
- •2. Кручение призматических стержней произвольного постоянного поперечного сечения
- •3. Приведение произвольной системы сил к простейшему виду. Условия равновесия произвольной системы сил.
- •1. Линейные однородные ду n-го порядка. Структура общего решения
- •2. Канонические уравнения движения системы
- •1. Уравнения Лапласа и Пуассона. Постановка граничных задач. Фундаментальное решение уравнения Лапласа. Функции Грина
- •2. Движение точки в поле центральных сил. Формулы Бине
- •3. Интегрирование дифференциального уравнения изогнутой оси балки
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Основные этапы решения задач механики в пакетах компьютерной механики (на примере пакетов ansys и nastran)
- •3. Двумерное стационарное движение газа. Уравнение Чаплыгина
- •1. Матрицы и действия над ними. Определители и их свойства. Обратная матрица. Матричная форма записи системы линейных уравнений. Метод Крамера
- •2. Устойчивость равновесия механической системы. Теорема Дирихле
- •3. Растяжение и сжатие стержня. Продольная сила. Условия прочности при растяжении.
- •1. Разностные схемы для ур-й мат физики. Явные и неявные разностные схемы, условия их устойчивости. Метод прогонки
- •2. Принцип Остроградского-Гамильтона
- •3. Канонические уравнения метода сил при изгибе балок и рам
- •1. Численные решения систем алгебраических уравнений. Метод исключения. Метод итераций. Теорема о сходимости
- •2. Слоистые течения вязкой жидкости. Течение Пуазейля. Течение под действием силы тяжести
- •3. Движение точки в поле центральных сил. Закон всемирного тяготения
- •1. Численное решение уравнений. Метод итерации, его сходимость. Метод Ньютона, его геометричсексий смысл
- •2. Определение траектории материальной точки в ньютоновом поле тяготения. Искусственные спутники Земли
- •3. Модель вязкой жидкости. Уравнения Навье - Стокса
- •1. Численное решение оду. Метод Рунге-Кутта
- •2. Принцип возможных перемещений. Уравнение Даламбера-Лагранжа
- •3. Задача о сильном взрыве в газе
- •1. Линейное уравнение n-го порядка с постоянными коэффициентами
- •2. Общие теоремы динамики системы материальных точек
- •3. Модель идеальной жидкости. Интегралы уравнений движения идеальной жидкости
- •1. Степенные ряды и их свойства. Интервал и радиус сходимости
- •2. Динамика точки переменной массы. Уравнение Мещерского. Задача Циолковского
- •3. Трансзвуковые течения. Уравнение Эйлера–Трикоми. Особенности сверхзвукового обтекания тел
- •1. Численное решение оду. Метод Рунге- Кутта
- •2. Методы четвертого порядка точности.
- •2. Устойчивость равновесия механической системы. Теорема Дирихле
- •3. Свойство упругого равновесия изотропного тела при отсутствии массовых сил
1. Степенные ряды и их свойства. Интервал и радиус сходимости
Опр.
Степенным рядом наз. ф-ный ряд вида:
![]() или
или![]() .
.
Лемма.
Если степ ряд (1) сход для
![]() ,
то он сход абсолютно для
,
то он сход абсолютно для
![]() уд н-ву
уд н-ву![]()
Следствие.
Если в некот т
![]() ряд
(1) расх, то он расх
ряд
(1) расх, то он расх
![]() :
:
![]()
Опр.
Пусть
![]() ,
где точная верхняя грань берется по
мн-ву всех аргументов
,
где точная верхняя грань берется по
мн-ву всех аргументов
![]() ,
при которых ряд сходится. Тогда
,
при которых ряд сходится. Тогда![]() наз
радиусом сходимости степ ряда (1). Круг
наз
радиусом сходимости степ ряда (1). Круг![]() наз кругом сходимости ряда (1). Если
наз кругом сходимости ряда (1). Если![]() ,
то ряд сх-ся
,
то ряд сх-ся![]() Если
Если![]() ,
то ряд сх-ся в одной т
,
то ряд сх-ся в одной т![]()
Теорема.
Степ ряд (1) сход равномерна на любом
замкн. Промежутке, лежащем внутри
интервала сходимости (![]() )
)
Замеч.
В точках окр-ти
![]() ряд (1) может как сходится так и расходится
ряд (1) может как сходится так и расходится
Теорема.
Если
![]() конечный предел
конечный предел
![]() ,
то радиус сх-ти степ ряда
,
то радиус сх-ти степ ряда![]() .
.
Теорема.
Радиус сх-ти степ ряда
![]() вычисл по ф-ле
вычисл по ф-ле
![]()
2. Динамика точки переменной массы. Уравнение Мещерского. Задача Циолковского
Систему
(тело), масса которой непрерывно изменяется
со временем принято называть сис-мой(телом)
переменной массы.
Если тело движется поступательно и
проходимые им расстояния велики, то
тело можно рассматривать как точку
переменной массы. Диф. ур-ние движения
точки переменой массы
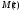 –
масса тела в моментt,
–
масса тела в моментt,
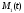 -
масса присоединяющихся точек,
-
масса присоединяющихся точек,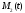 - масса отделяющихся точек. Система
состоит из
- масса отделяющихся точек. Система
состоит из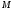 ,
,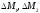 ,
причём сис-мы они образуют лишь в момент
времениt.
Результат наших рассуждений будет
корректным если
,
причём сис-мы они образуют лишь в момент
времениt.
Результат наших рассуждений будет
корректным если
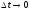
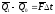 (теорема об изменении главного вектора
количества движения)
(теорема об изменении главного вектора
количества движения)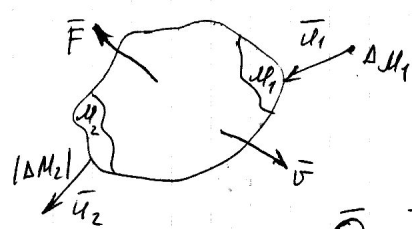
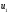 -
абсолютная скорость присоединяющихся
точек
-
абсолютная скорость присоединяющихся
точек
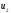 -
абсолютная скорость отделяющихся точек
-
абсолютная скорость отделяющихся точек
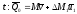
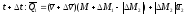
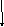
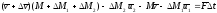 - деля обе части
равенства на
- деля обе части
равенства на
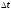 и
переходя к пределу
и
переходя к пределу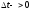 получим:
получим: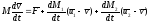 -
уравнение Мещерского.
-
уравнение Мещерского.
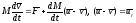 -относительная
скорость присоединения(отделения)
-относительная
скорость присоединения(отделения)
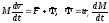 - реактивная сила
- реактивная сила
1-я
задача Циолковского – определение
закона поступательного движения ракеты
вне поля сил (т.о. полагаем
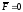 ).
Уравнение Мещерского принимает вид:
).
Уравнение Мещерского принимает вид:
![]() =>
=>
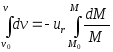 =>
Считая относительную скорость истечения
продуктов сгорания
=>
Считая относительную скорость истечения
продуктов сгорания постоянной
и полагая при
постоянной
и полагая при результат интегрирования
результат интегрирования![]() - з-н изменения скорости.
- з-н изменения скорости.![]() -
масса корпуса,
-
масса корпуса,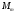 -
масса топлива,
-
масса топлива,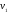 -
скорость ракеты в конце активного
участка.
-
скорость ракеты в конце активного
участка.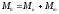 =>
=>![]() - ф-ла Циолковского,
- ф-ла Циолковского,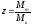 -
число Циолковского. Предельная скорость
зависит от начальной скорости, от
скорости истечения продуктов сгорания,
числа Циолков-го и не зависит от режима
сгорания топлива.
-
число Циолковского. Предельная скорость
зависит от начальной скорости, от
скорости истечения продуктов сгорания,
числа Циолков-го и не зависит от режима
сгорания топлива.![]() =>
=>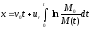
2-я
задача Циолковского – определение
закона движения в однородном поле силы
тяжести
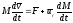
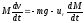 =>
=>![]() -
з-н сгорания топлива (
-
з-н сгорания топлива (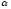 -
постоянный коэффициент, характеризующий
скорость изменения массы) =>
-
постоянный коэффициент, характеризующий
скорость изменения массы) =>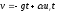 =>
вертикальный подъем возможен при
=>
вертикальный подъем возможен при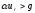 ,
,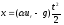 .
.
3. Слоистые течения. Течение Пуазейля, течение Куэтта, течение под действием силы тяжести
Класс
точных решений урвынений Новье-Стокса
давольно узок.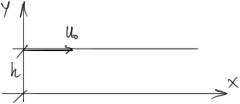
1.Течение
Куэтта- течение между параллельными
стенками,одна из которых движется с
постоянной скоростью
![]() Массовые
силы отсутствуют,движение жидкости
между стенками называют движением
верхней границы.
Массовые
силы отсутствуют,движение жидкости
между стенками называют движением
верхней границы.
![]()
![]()
![]()
![]() ;
;![]() ;
;![]() ; =>
; =>![]()
![]() =>
=>![]() =>
=>![]() ;
;
![]() -
начальные условия
-
начальные условия ![]()
Стационарное
решение:
![]() ;
;![]() из 1го условия
из 1го условия
![]()
![]() -
линейный профиль;
-
линейный профиль;![]() -
значение Ньютона
-
значение Ньютона
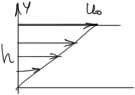
Расход
жидкости через поперечное сечение
![]() :
:
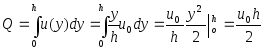
Средняя
скорость-расход жидкости на площадь
попер. Сечения 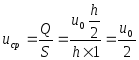
2. Течение между двумя параллельными стенками под действиемперепада давления- течение Пуазейля.
![]() ;
;
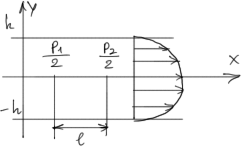
![]()
Решение
ищем в виде:
![]()
![]()
 -
уравнение неразрывности тождественно
выполняется =>
-
уравнение неразрывности тождественно
выполняется =>![]()
При
![]() при
при![]() -
условие прилипания.
-
условие прилипания.![]() -
стационарная задача
-
стационарная задача
![]() делим на
делим на
![]() :
:![]()
![]()
![]() ;
;![]()
![]()
![]() =>
=> ![]() h
всегда>y
h
всегда>y
Максимальная скорость при y=0
3. Течение вязкой жидкости под действием силы тяжести.
Линии
тока параллельны OX: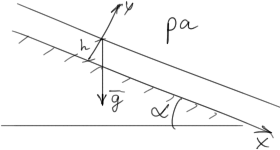
![]()
![]() (
(![]() ;
;![]() )
)
![]()
Граничные
условия: ![]()
![]() -
свободная поверхность ;
-
свободная поверхность ;
![]() -
уравнение неразрывности;
-
уравнение неразрывности;![]() (нормальные
напряжения) касательные=0 т.к.
(нормальные
напряжения) касательные=0 т.к.![]() - отсутствуют касательные напряжения
- отсутствуют касательные напряжения
![]()
![]()
Будем
считать,что движение формируется лишь
под действием силы тяжести:
![]()
а
![]() -стационарная задача
-стационарная задача
![]()
![]()
![]() при y=h
при y=h
![]() при
при![]()
![]() ;
;![]() при
при![]()
Билет
17
1.
Сопровождающий трехгранник кривой.
Кривизна и кручение. Формулы
Френе
Параметризация.
Фигура
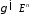 называетсякривой,
если для любой точки
называетсякривой,
если для любой точки
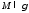 существует окрестность
существует окрестность в
в и отображение
и отображение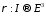 такое, что: 1)
такое, что: 1) взаимно непрерывное отображение 2)
взаимно непрерывное отображение 2)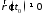 При
этом пара
При
этом пара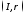 наз-сяпараметризацией
окрестности
наз-сяпараметризацией
окрестности
![]() в
в![]() .
Параметрическая криваярегулярна,
если в любой точке этой кривой
.
Параметрическая криваярегулярна,
если в любой точке этой кривой
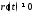 ,
ибирегулярна
, если
,
ибирегулярна
, если
 не коллинеарен
не коллинеарен ,
т.е.
,
т.е.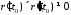 .
.
Репер
Френе. Репер
— тройка некомпланарных (непараллельных
одной плоскости) векторов.
Пусть задана
бирегулярная кривая
 ,
тогда с любой точкой
,
тогда с любой точкой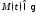 можно связать репер
можно связать репер ,
,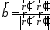 ,
,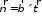 ,
где
,
где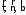 — касательная, нормаль и бинормаль.
Плоскость, образованная
— касательная, нормаль и бинормаль.
Плоскость, образованная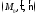 —
соприкасающаяся,
—
соприкасающаяся,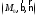 —
нормальная,
—
нормальная,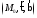 —
спрямляющая.
—
спрямляющая.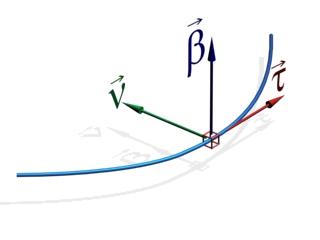
Натуральная
параметризация.
Параметризация
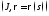 называетсянатуральной,
если
называетсянатуральной,
если
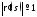 (значит,
точка движется с единичной скоростью,
то есть при деформации длина интервала
не меняется). Такая параметризация
всегда существует.
(значит,
точка движется с единичной скоростью,
то есть при деформации длина интервала
не меняется). Такая параметризация
всегда существует.
Длина
дуги. Длиной
дуги
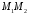 кривой
кривой называется
число
называется
число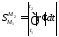
Кривизна.
Пусть —
регулярная кривая с натуральной
параметризацией
—
регулярная кривая с натуральной
параметризацией и пусть
и пусть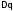 —
угол между касательными в точках
—
угол между касательными в точках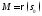 и
и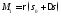 .Тогда
величина
.Тогда
величина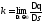 наз-сякривизной,
а
наз-сякривизной,
а
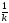 радиусом
кривизны
кривой
радиусом
кривизны
кривой
![]() в точке
в точке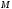 (это скорость поворота касательной при
движении точки по кривой).
(это скорость поворота касательной при
движении точки по кривой).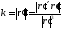 для натуральной и произвольной
параметризаций соответственно.
для натуральной и произвольной
параметризаций соответственно.
Кручение.
Пусть![]() —
регулярная кривая с натуральной
параметризацией
—
регулярная кривая с натуральной
параметризацией![]() и пусть
и пусть![]() —
угол между бинормалями в точках
—
угол между бинормалями в точках![]() и
и .Тогда
величина
.Тогда
величина наз-сякручением
кривой
наз-сякручением
кривой
![]() в точке
в точке![]() (это скорость поворота вектора бинормали).
(это скорость поворота вектора бинормали).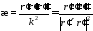 для натуральной и произвольной
параметризаций соответственно.
для натуральной и произвольной
параметризаций соответственно.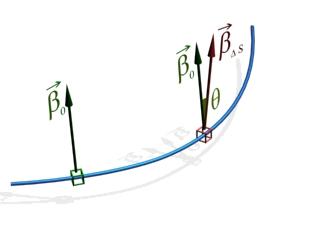
Формулы
Френе.
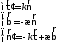 —
для натуральной пар-ции
—
для натуральной пар-ции —в
матр. виде
Формулы Френе задают
разложение произвольных базисных
векторов репера Френе по базису Френе.
Задать формулы Френе — значит задать
кривизну и кручение.
—в
матр. виде
Формулы Френе задают
разложение произвольных базисных
векторов репера Френе по базису Френе.
Задать формулы Френе — значит задать
кривизну и кручение.
