Решение уравнений с параметром

Предположим, что нужно решать уравнение многократно при изменении одного из параметров этого уравнения. Например, пусть требуется решить уравнение e^x=ax² для нескольких различных значений параметра a. Самый простой способ состоит в определении функции f(a,x)= root(e^x - ax²,x).

Чтобы решить уравнение для конкретного значения параметра a, присвойте значение параметру a и начальное значение переменной x как аргументам этой функции. Затем найдите искомое значение корня, вводя выражение f(a,x)=.

ПРИМЕР 3. Найти решение уравнения ex =ax³ при различных значениях a.

1. Определите функцию f, решающую уравнение для заданного a: f(a,x):=root(e^x -a∙x³ ,x).

2. Задайте значения a как промежуток от 1 до 20: a:=1..20.

3. Задайте начальное приближение, введя строку x₀:=1.

4. Определите общую формулу для нахождения x_a следующим образом: x_a:=f(a, x_a-1). Таким образом, начальное приближение для каждого есть корень, соответствующий предыдущему a.

5. Выведите значения a и соответствующие им x_a, набрав а= и х_а=.

6. Сделайте проверку, то есть выведите значения левой и правой частей уравнения при х=х_а.

Нахождение корней полинома

Для нахождения корней выражения, имеющего вид v_n xⁿ+...+v₂ x²+v₁ x+v₀, можно использовать функцию polyroots. В отличие от функции root, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные.

Функция polyroots (v) возвращает корни полинома степени n. Коэффициенты полинома находятся в векторе v длины n+1. Сюда должны войти все коэффициенты, в том числе равные нулю. Первым в векторе должен идти свободный член полинома (т.е. коэффициент при х⁰), вторым – коэффициент при х¹ и т.д. соответственно, последним n+1 элементом вектора должен быть коэффициент при старшей степени xⁿ.

Функция polyroots возвращает вектор длины n, состоящий из корней полинома.

ПРИМЕР 4. Найдем решение уравнения x³ - 10*x+2 = 0.

1. Сформируйте вектор коэффициентов 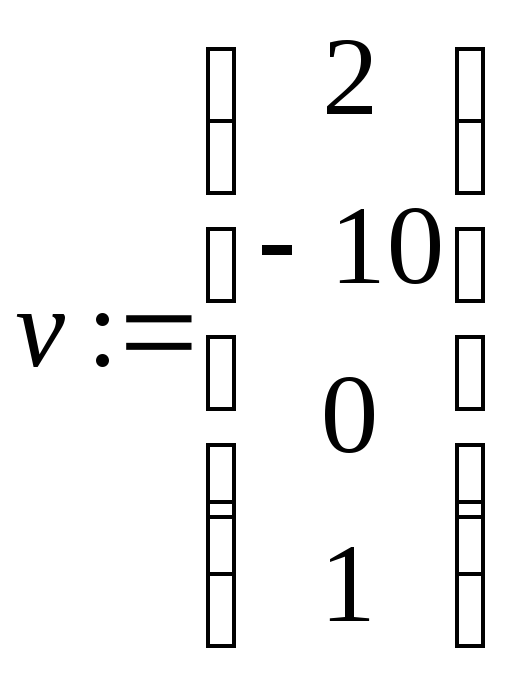, перечислив коэффициенты в порядке возрастания степени переменнойх.

2. Найдите корни уравнения с помощью функции polyroots с параметром v, набрав polyroots(v)=.

3. Сделайте проверку.

ЗАДАНИЕ 1. Найти решение уравнения x3 + (3+2i)x2 + (-4+6i)x - 8i = 0.

Системы уравнений

Mathcad дает возможность решать также и системы N уравнений с M неизвестными

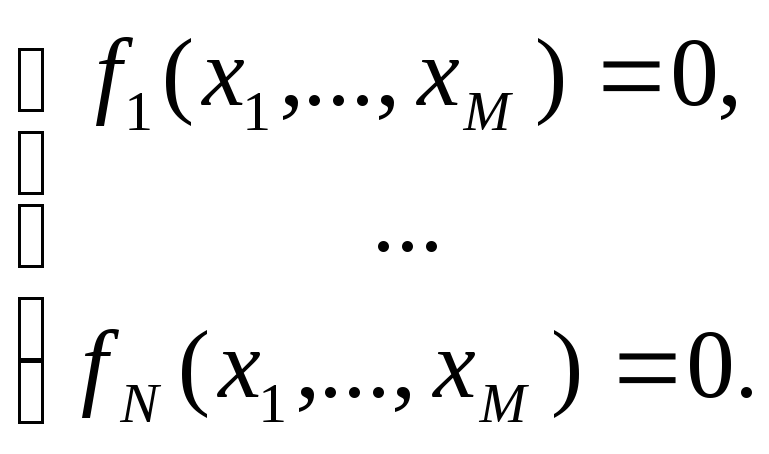
Для решения систем уравнений имеется специальный вычислительный блок, состоящий из трех частей, идущих последовательно друг за другом:

• Given – ключевое слово;

• система, записанная логическими операторами в виде равенств и, возможно, неравенств;

• Find (x₁,…,x_M) – встроенная функция для решения системы относительно переменных х₁,…,х_М.

Блок Given\Find использует для поиска решения итерационные методы, поэтому, как и для функции root, требуется задать начальные значения для всех х₁,…,х_М. Сделать это необходимо до ключевого слова Given.

Значение функции Find есть вектор, составленный из решения по каждой переменной.

Для решения системы уравнений или неравенств выполните следующее:

1. Задайте начальные приближения для всех неизвестных, входящих в систему уравнений или неравенств.

2. Напечатайте ключевое слово Given (можно использовать любой шрифт, прописные и строчные буквы).

3. Введите уравнения или неравенства ниже ключевого слова Given. Удостоверьтесь, что между левыми и правыми частями уравнений или неравенств стоят символы логических операторов. Между левыми и правыми частями неравенств может стоять любой из символов “=”, “<”, “>”, “” и “”.

4. Введите любое выражение, которое включает функцию Find (можно использовать шрифт любого размера, прописные и строчные буквы).

ПРИМЕР 5. Решить систему уравнений x⁴+y²-3=0 и x+2y=0.

1. Задайте начальные значения переменных: x:=1, y:=1.

2. Напишите слово Given, после которого в следующих строках запишите уравнения системы. Для ввода символа “=” используйте панель логических операторов или нажмите <Ctrl>+<=>.

3. В следующей строке поместите выражение a:=Find(x,y). Таким образом, в переменную a будет занесено решение этого уравнения.

4. Выведите результат (наберите а=) и сделайте проверку.

ПРИМЕР 6. Найти точки пересечения окружности x²+y²=6 и прямой x+y=2.

1. Задайте начальные значения переменных: x:=1, y:=1.

2. Напишите слово Given.

3. Введите ниже уравнения окружности и прямой.

4. Выведите координаты точки пересечения прямой с окружностью, набрав Find(x, y)=.

5. Сделайте проверку.

6. Задайте новые начальные значения следующим образом: x:=-1, y:=1.

7. Выполните шаги 2-4 и сравните полученные ответы.

Блоки решения уравнений не могут быть вложены друг в друга. Каждый блок решения уравнений может иметь только одно ключевое слово Given и имя функции Find. Можно, однако, определить функцию f(x):=Find(x) в конце одного блока решения уравнений и затем использовать f(x) в другом блоке.

ЗАДАНИЕ 2. Решить систему уравнений, задав начальные приближения для неизвестных, равные 1.

0,21x₁-0,45x₂-0,20x₃=1,91;

0,30x₁+0,25x₂+0,43x₃=0,32;

0,60x₁-0,35x₂-0,25x₃=1,83.