Вычисление сумм и произведений

Чтобы найти сумму или произведение в численном или символьном виде:

1. Вызовите оператор суммирования или произведения , используя панель Вычисления (Calculus).

2. Введите выражение в месте ввода справа от «» или «П».

3. Поместите индекс и диапазон изменения индекса в поля выше и ниже.

4. Окружите всё выражение выделяющей рамкой и введите знак = (для численного вычисления) или оператор  (для символьного).

Если при вычислении суммы или произведения используются числовые пределы, проверьте, чтобы верхний предел был больше или равен нижнему.

ЗАДАНИЕ 8. Проверьте символьное вычисление:

1.;

2. .

ЗАДАНИЕ 9. Используя операторы суммирования и перемножения, вычислить:

1. Сумму и произведение натуральных чисел в диапазоне от 5 до 12.

2. Сумму и произведение четных чисел в диапазоне от -10 до 10.

3. Сумму и произведение нечетных чисел в диапазоне от 5 до 31.

4. Сумму и произведение квадратов синусов углов, изменяющихся в диапазоне от 0 до 180^о с шагом 10^о.

5. Сумму элементов вектора произвольной длины.

6. Сумму элементов прямоугольной матрицы произвольной размерности.

Вычисление производных

Mathcad предлагает два оператора для нахождения численного значения производных функции в заданной точке: оператор для нахождения первой производной и универсальный оператор для нахождения производной n‑го порядка.

Чтобы найти производную функции в точке:

1. Определите точку х, в которой нужно найти производную, например, х:=1.

2. Ниже определения точки введите оператор дифференцирования, нажав кнопку на панели Вычисления (Calculus) или нажмите клавишу <?>.

3. Введите в местозаполнитель в знаменателе имя переменной х, а во второй месозаполнитель – функцию, зависящую от х, например, cos(x)·ln(x).

4. Введите оператор численного <=> или символьного <> вывода для получения ответа.

Замечание. Для численного дифференцирования обязательно предварительно нужно определить точку, в которой вычисляется производная. Иначе будет выдано сообщение об ошибке. Между тем символьное дифференцирование не требует обязательного явного задания точки дифференцирования. В этом случае вместо числового значения производной будет выдана аналитическая зависимость.

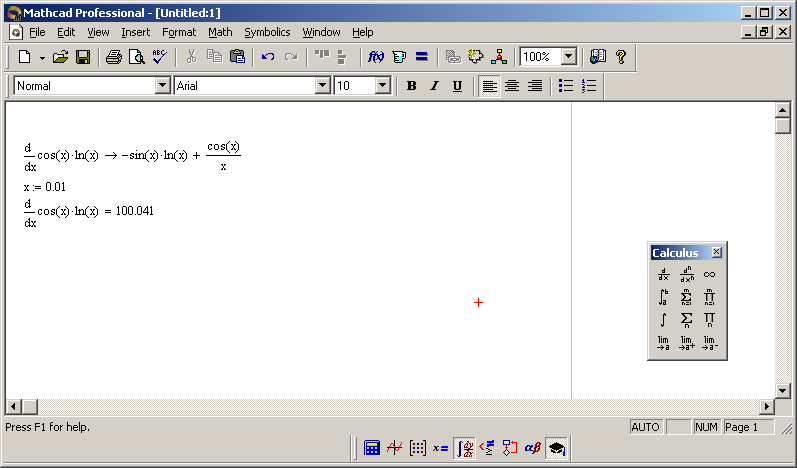
Рис. 21. Численное и символьное дифференцирование

Можно, как и при использовании других операторов, предварительно определить функцию в отдельном выражении, а затем посчитать ее производную.

Чтобы найти производную n-го порядка:

1. Определите точку, в которой необходимо найти производную.

2. Ниже определения точки введите оператор дифференцирования, нажав кнопку на панели Вычисления (Calculus) или нажмите клавиши <Ctrl>+<?>.

3. Введите в местозаполнитель в знаменателе имя переменной, по которой производится дифференцирование.

4. В местозаполнитель выше и правее от предыдущего введите порядок производной. Это должно быть целое число от 0 до 5. Обратите внимание, что поле в числителе автоматически отображает любой порядок, печатаемый в знаменателе.

5. В последний местозаполнитель введите выражение, которое нужно дифференцировать.

6. Введите оператор численного <=> или символьного <> вывода для получения ответа.

При n=1 этот оператор дает тот же самый результат, что и рассмотренный ранее оператор производной. При n=0 возвращается значение функции.

Хотя дифференцирование возвращает только одно число, можно определить одну функцию как производную другой функции. Например, вычислениеF(x) будет возвращать в численной форме производную g(x) в точке х. Эта методика может быть использована для вычисления производной функции в последовательности точек.

Замечание. Чтобы вычислить производную порядка выше 5-го, следует последовательно применить несколько раз оператор n-й производной. Однако символьный процессор умеет считать производные порядка выше 5-го.

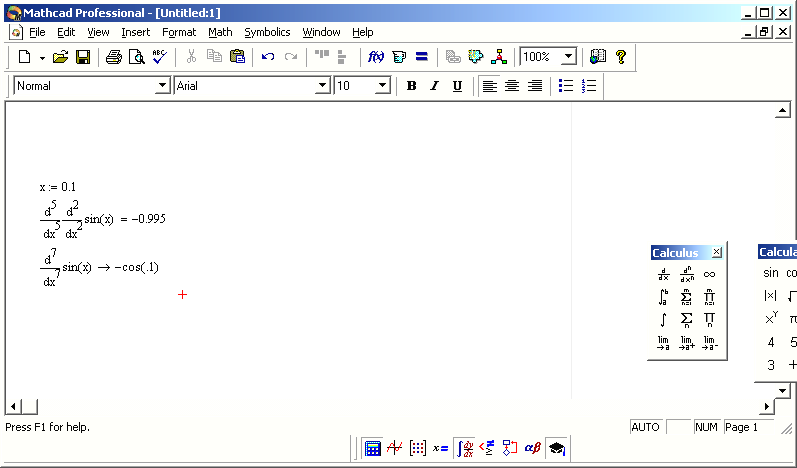
Рис. 22. Численное и символьное вычисление седьмой производной

ЗАДАНИЕ 10. Вычислить, используя операторы численного дифференцирования:

1. Первую и третью производные функции Y = 5*x⁸ в точке x=3.

2. Первую и третью производные функции Y = 5*x⁸ для всех четных значений х в диапазоне от 10 до 20.

3. Первую и третью производные функции Y = 5*x⁸ для 5 значений х: 1; 2.5; 3.8; 4.2; 12.4.