Векторные и матричные функции

Получение из массива или скаляра матрицы специального типа

identity (n)	Единичная матрица (nxn), диагональные элементы равны 1, все остальные равны 0.
diag(v)	Диагональная матрица, содержащая на диагонали элементы вектора v.

Размер и диапазон значений массива

rows(A)	Число строк в массиве А. Если А – скаляр, возвращается 0.
cols(A)	Число столбцов в массиве А. Если А – скаляр, возвращается 0.
length(v)	Число элементов в векторе v.
last(v)	Индекс последнего элемента в векторе v.
max(A)	Максимальный элемент в массиве А.
min(A)	Минимальный элемент в массиве А.

Формирование новых матриц из существующих

augment(A,B)	Матрица, сформированная расположением А и В бок о бок. Матрицы должны иметь одинаковое число строк
submatrix (A,ir,jr,ic,jc)	Субматрица, состоящая из всех элементов, содержащихся в строках с irпоjrи столбцахcicпоjc(ir<=jrиic<=jc).
stack(A,B)	Матрица, сформированная расположением А над В. Матрицы должны иметь одинаковое число столбцов

Специальные характеристики матрицы

tr (A)	Сумма элементов диагонали, называемая следомматрицы.
rank(A)	Ранг матрицы А.

Задание 5. Выполните вычисления с массивами:

1. Даны матрицы: .

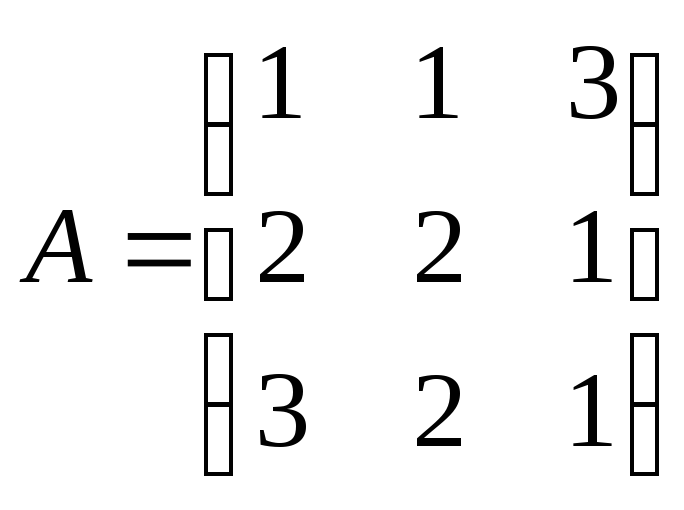
Найти: а) 2А²–3В; б) А·В; в) f(B), если f(x)=x²–2x+5.

2. Для матрицы 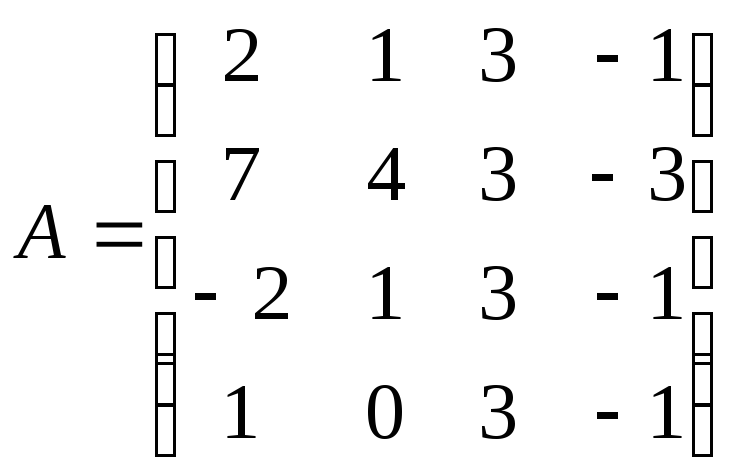вычислите:а) определитель матрицы А; б) 7А; в) А^-1; г) А^T; д) максимальный элемент матрицы А^-1; е) минимальный элемент матрицы А^-1.

3. Даны

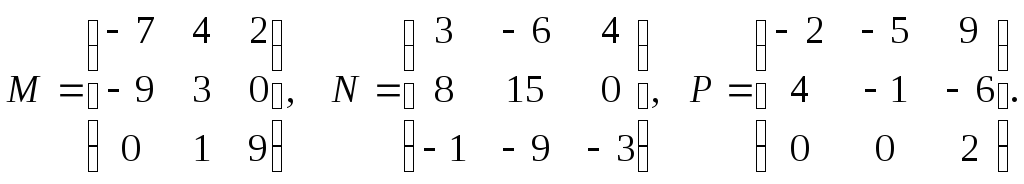
Найдите: а) M*(N + P); б) |M - N|; в) (M - P) ^-1; г) M ^T + N ^T – P ^T.

4. Даны матрицы:.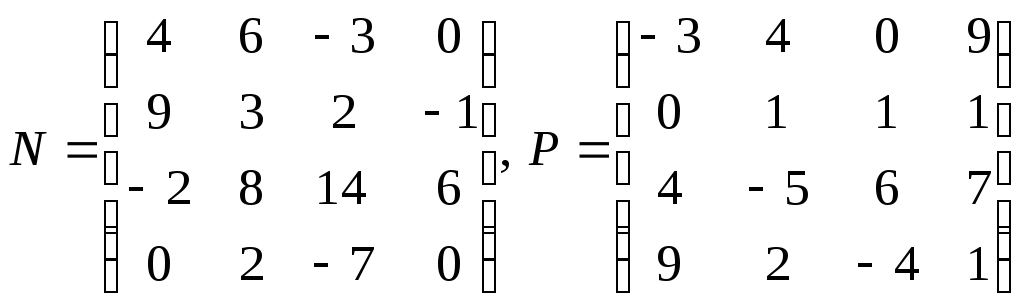

Найдите: а) N + P; б) N * P; в) определитель матрицы P-N.

Контрольная работа №2

1. Создать матрицу W размерностью 9х10, заполнить произвольными числовыми значениями.

2. Извлечь из матрицы W:

• 8-й столбец;

• 4-ю строку;

• матрицу U, содержащую строки с 3-й по 7-ю и столбцы с 4-го по 6-й матрицы W;

• матрицу X, содержащую строки с 1-й по 4-ю и столбцы с 1-го по 10-й матрицы W;

• матрицу Y, содержащую строки с 1-й по 9-ю и столбцы с 1-го по 4-й матрицы W.

3. Создать матрицу A путем транспонирования матрицы W.

4. Определить количество строк и столбцов в матрицах W, A и U.

5. Определить наибольшее и наименьшее значения элементов в матрицах W, A и U.

6. Создать матрицу В путем “горизонтального” объединения матриц W и Y.

7. Создать матрицу C путем “вертикального” объединения матриц W и X.

8. Создать матрицу Е, каждый элемент которой равен квадратному корню из соответствующего элемента матрицы А.

9. Создать вектор V размером 10, в котором значение каждого элемента равно третьей степени значения его индекса.

10. Создать вектор Q, каждый элемент которого вдвое меньше соответствующего элемента вектора V.

11. Вычислить скалярное произведение векторов V и Q.

12. Создать вектор Р, каждый элемент которого содержит произведение соответствующих элементов векторов V и Q.

13. Определить длины векторов V и Q и значения индексов их последних элементов.

14. Создать диагональную матрицу на базе вектора V.

15. Преобразовать векторы-столбцы P, Q, V в соответствующие векторы-строки. Определить их длины и значения индексов последних элементов.

16. Создать матрицу 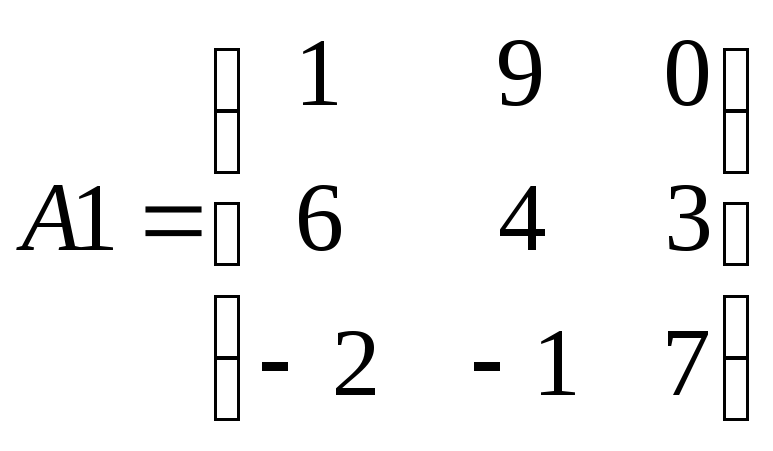и вектор.

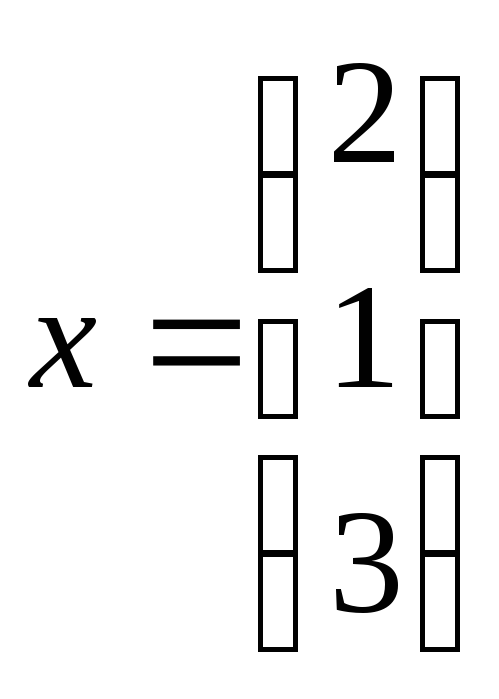• вычислите произведение A1 на x;

• сформируйте матрицу B1 размерностью 3х3 по правилу b_i,j=(i²+3j²)/2;

• вычислите произведения матриц A1*B1 и B1*A1, записав их, соответственно, в матрицы Z1 и Z2;

• вычислите произведение вектора x и матрицы Z1.

17. Найти ранг заданной матрицы A2 и обратную матрицу (если это возможно).

а) ; в) ;

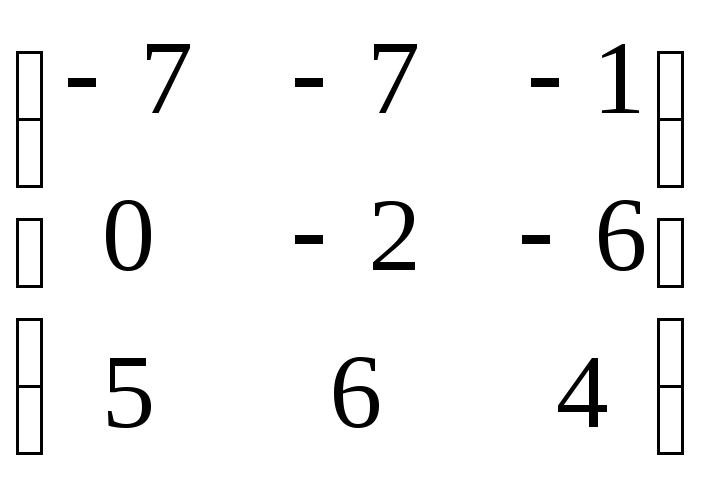б) ; г) .
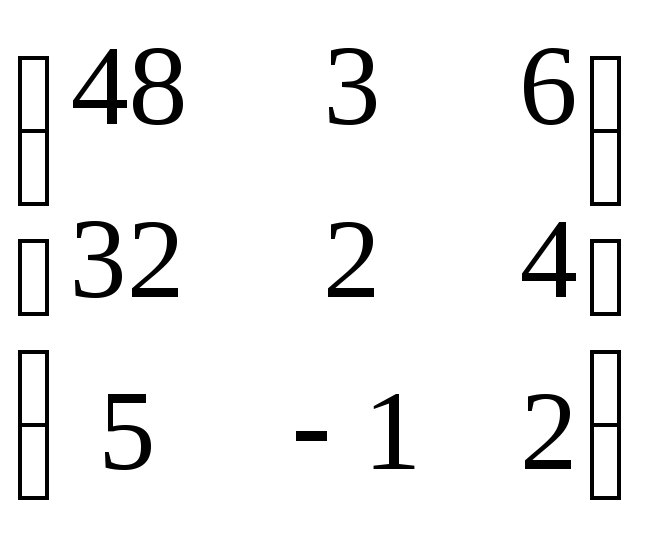