
- •Основы работы
- •В математическом пакете Mathcad
- •Методические рекомендации
- •Для проведения лабораторных работ
- •Лабораторная работа № 1 Знакомство с Mathcad
- •Документы и окна
- •Типы данных
- •Построение выражений
- •Некоторые приемы редактирования выражений
- •Ввод текста
- •Форматирование выражений и результатов
- •Защита вычислений
- •Лабораторная работа № 2 Переменные и функции Определение переменных и функций
- •Определение дискретной переменной
- •Глобальные определения переменных и функций
- •Вычисления с использованием единиц измерения
- •Контрольная работа №1
- •Лабораторная работа № 3. Массивы
- •Создание массива командой Вставка матрицы
- •Определение переменных как массивов
- •Доступ к элементам массива
- •Изменение размера матрицы
- •Создание массива путем определения его элементов
- •Создание матрицы с помощью дискретных аргументов
- •Векторные и матричные операторы
- •Векторные и матричные функции
- •Задание 5. Выполните вычисления с массивами:
- •Контрольная работа №2
- •Лабораторная работа № 4 Графика в Mathcad Двухмерные графики Графики в декартовой системе координат
- •Форматирование двухмерных графиков
- •Трассировка и масштабирование
- •Графики в полярной системе координат
- •Трехмерные графики
- •Применение Мастера построения трехмерных графиков
- •Специальная графика
- •Создание и запуск анимационных клипов
- •Контрольная работа №3
- •Лабораторная работа № 5 Создание программ
- •Условный оператор
- •Цикл while
- •Оператор break
- •Цикл for
- •Пример 8. Составить функцию для суммирования целых чисел от 1 до n.
- •Подпрограммы
- •Задание 26. Составить функцию для вычисления суммы факториалов, оформив в виде подпрограммы нахождение факториала числа.
- •Задание 29. Найти все простые числа на заданном отрезке.
- •Контрольная работа №4
- •Лабораторная работа № 6 Решение уравнений Решение уравнения с одним неизвестным
- •Решение уравнений с параметром
- •Нахождение корней полинома
- •Системы уравнений
- •Матричный способ решения систем уравнений
- •Приближенные решения
- •Символьное решение уравнений
- •Контрольная работа №5
- •Лабораторная работа № 7 Символьная математика
- •Упрощение выражения
- •Разложение выражений
- •Разложение выражения на множители
- •Приведение подобных слагаемых
- •Разложение на элементарные дроби
- •Разложение в ряд Тейлора
- •Вычисление сумм и произведений
- •Вычисление производных
- •Вычисление определенного интеграла
- •Неопределенные интегралы
- •Пределы
- •Подстановка переменной
- •Отображение результатов символьных вычислений
- •Контрольная работа №6
- •Список литературы
- •Содержание
- •Тетюшева Светлана Геннадьевна
Контрольная работа №5
1. Построить график функции f(x) и приблизительно определить один из корней уравнения. Решить уравнение f(x)=0 с точностью ε=10- 4 с помощью функции root.
а) e x-1 – x 3 – x, x[0,1]; з) 0.25 x 3 + x – 2, x[0,2];
б) 3 x – 4 ln x – 5, x[2,4]; и) e x – e –x – 2, x[0,1];
в)
![]() ,
x[0,1]; к)
1–x+sin
x–ln(1
+ x),
x[0,2];
,
x[0,1]; к)
1–x+sin
x–ln(1
+ x),
x[0,2];
г)![]() ,
x[0,1]; л)
0.1 x
2 – x
ln
x,
x[1,2];
,
x[0,1]; л)
0.1 x
2 – x
ln
x,
x[1,2];
д)
![]() ,
x[0,1]; м)
,
x[0,1]; м)
![]() ,
x[2,3];
,
x[2,3];
е)
![]() ,
x[0,1]; н)
x
5 – x
– 0.2, x[1,2];
,
x[0,1]; н)
x
5 – x
– 0.2, x[1,2];
ж)
![]() ,
x[0,1]; о)
3 x
– 14 + e
x
– e
–x,
x[1,3].
,
x[0,1]; о)
3 x
– 14 + e
x
– e
–x,
x[1,3].
2. Решите уравнения, используя встроенную функцию root:
а) x3 – exp(x) = 0; б) x3 – 10 x2 + 2 x = 0;
в) 4 (1 – x2) – exp(x) = 0; г) x3 – 1.1 x2 – 2.2 x + 1.8 = 0.
Примечание. При решении уравнения постройте график. Если уравнение имеет несколько корней, используйте различные начальные приближения. Выполните контроль правильности решения.
3. Решите уравнения с параметром, используя функцию root:
а) exp(x) – a x2 = 0, a = 1, 2 .. 20;
б) exp(-a x2) – 2 x = 0, a = -0.5, -0.4 .. 2.
4. Используя функцию polyroots, найдите корни полинома:
а) x4 – 2 x3 + x2 - 12 x + 20; з) x4 + x3 -17 x2 - 45x – 100;
б) x4 + 6 x3 + x2 - 4 x –60; и) x4 - 5 x3 + x2 - 15x + 50;
в) x4 - 14 x2 - 40 x – 75; к) x4 - 4 x3 – 2 x2 - 20x + 25;
г) x4 - x3 + x2 - 11 x + 10; л) x4 + 5 x3 + 7 x2 + 7x – 20;
д) x4 - x3 – 29 x2 - 71 x – 140; м) x4 - 7 x3 + 7 x2 - 5x + 100;
е) x4 + 7 x3 + 9 x2 + 13 x – 30; н) x4 + 10 x3 + 36 x2 + 70x + 75;
ж) x4 + 3 x3 + 23 x2 - 55 x – 150; о) x4 + 9 x3 + 31 x2 + 59x + 60.
5. Решить систему линейных уравнений:
используя функции Find;
матричным способом, используя функцию lsolve.
а)
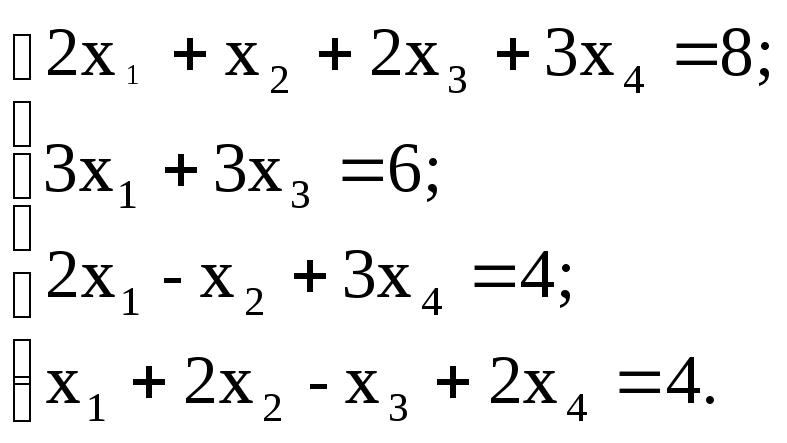 д)
д)
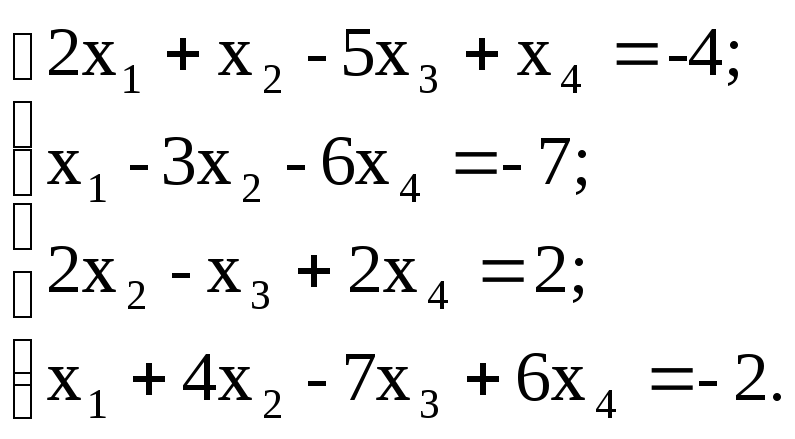
б)
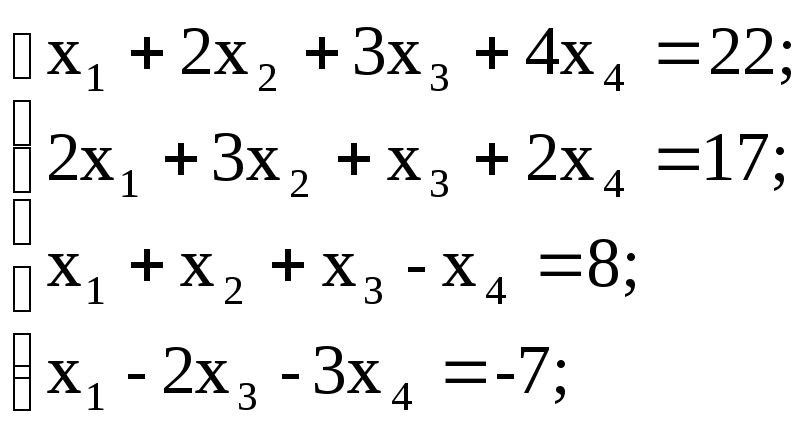 е)
е)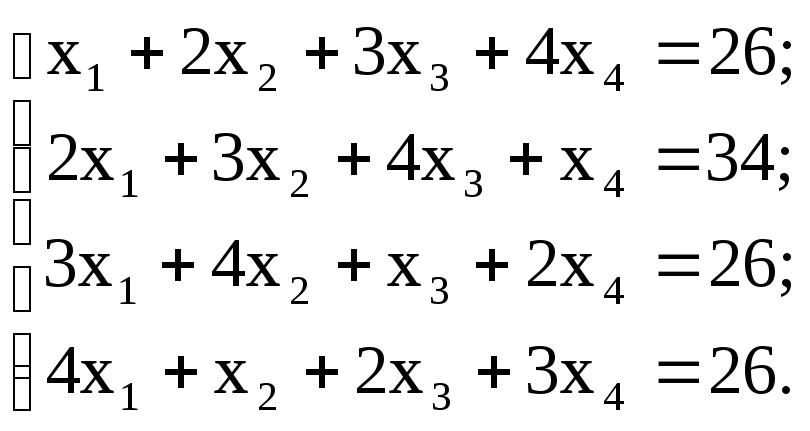
в)
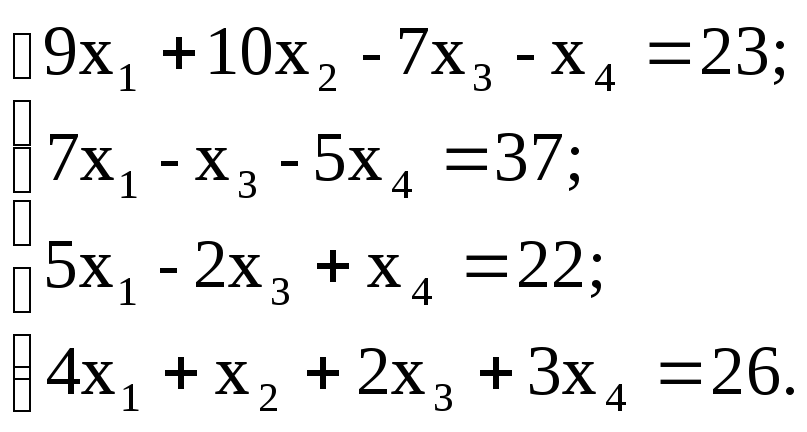 ж)
ж)
г)
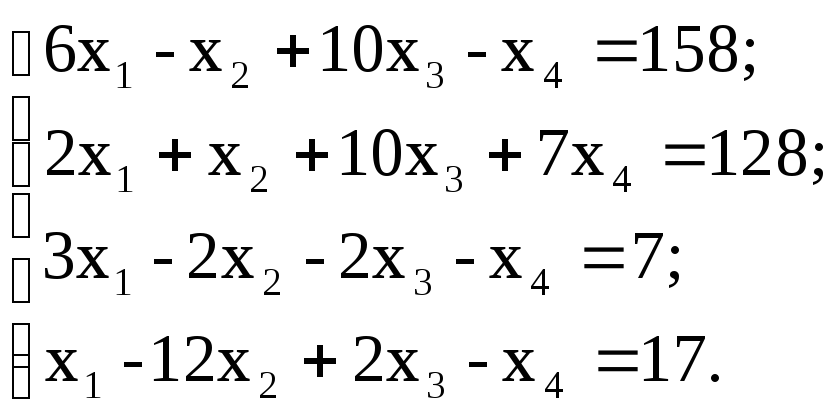 з)
з)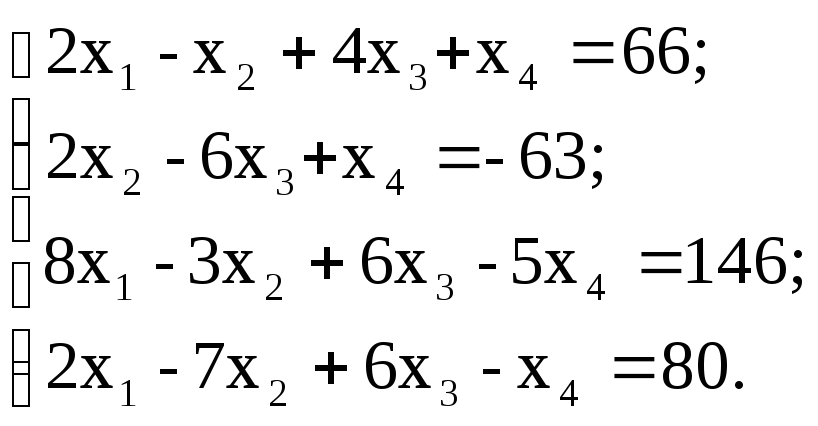
6. Преобразовать нелинейные уравнения системы к виду f1(x)=y и f2(y)=x. Построить их графики и определить начальное приближение решения. Решить систему нелинейных уравнений с помощью функции Minerr.
|
№ |
Система уравнений |
№ |
Система уравнений |
№ |
Система уравнений |
|
1 |
sin x+2y=2 cos(y-1)+x=0.7 |
6 |
cos(x+0.5)-y=2 sin y-2x=1 |
11 |
cos(x+0.5)+y=1 sin y-2x=2 |
|
2 |
cos x + y=1.5 2x-sin(y-0.5)=1 |
7 |
cos(x+0.5)+y=1 sin(y+0.5)-x=1 |
12 |
sin x – 2y=1 sin(y-1)+x=1.3 |
|
3 |
sin(x-1)=1.3-y x-sin(y+1)=0.8 |
8 |
2y-sin(x-0.5)=1 cos y + x=1.5 |
13 |
sin(x+2)-y=1.5 cos(y-2)+x=0.5 |
|
4 |
-sin(x+1)+y=0.8 sin(y-1)+x=1.3 |
9 |
sin(x+0.5)-y=1 cos(y-2)+x=0 |
14 |
cos(x-2)+y=0 sin(y+0.5)-x=1 |
|
5 |
sin y +x=-0.4 2y-cos(x+1)=0 |
10 |
cos(x+0.5)+y=0.8 sin y-2x=1.6 |
15 |
sin x – 2y=1 cos(y+0.5)-x=2 |
7. Решите системы уравнений:
а) ![]() г)
г) 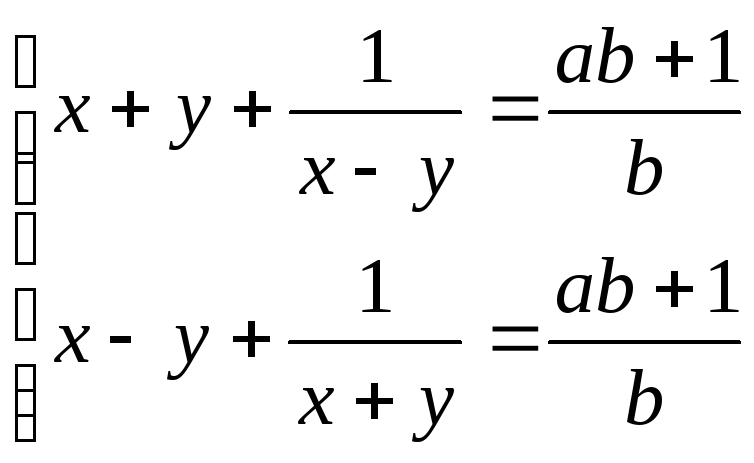
б) 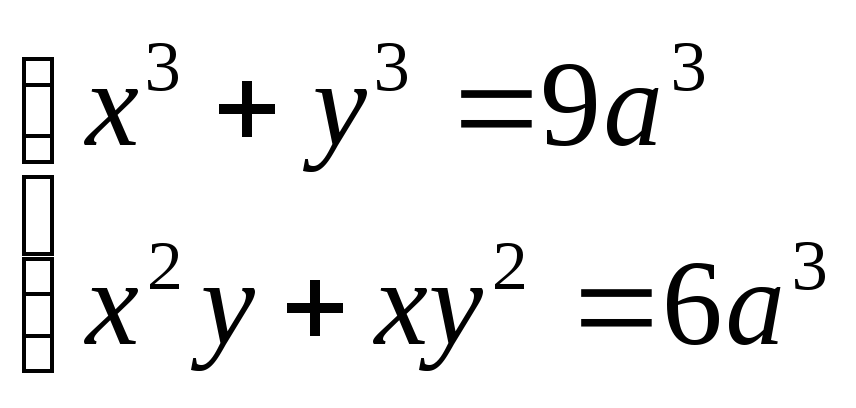 д)
д) ![]()
в) ![]() е)
е) 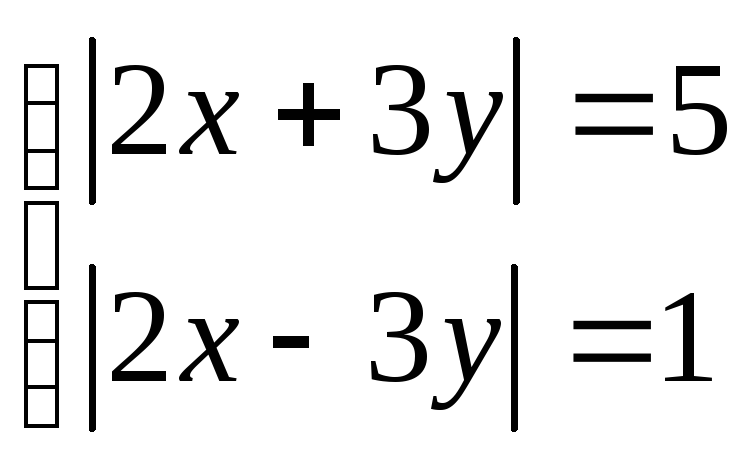
8. Решить системы уравнений в символьном виде:
а)
![]() б)
б)
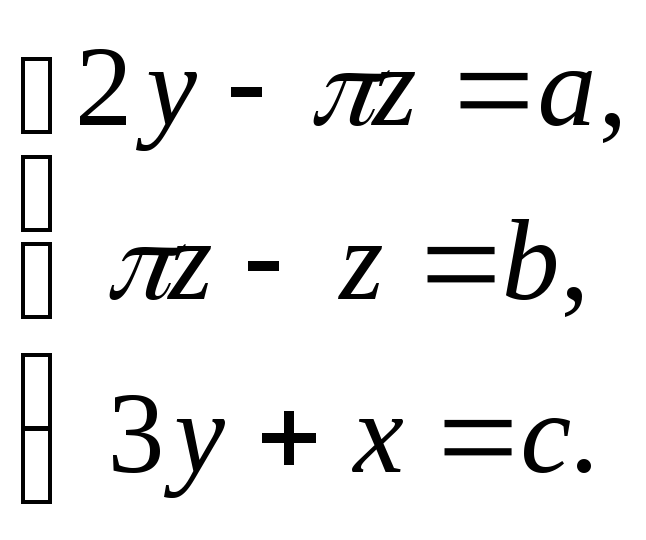
9. Решить неравенства:
а) a 4 + a 3 - a – 1 < 0; г) 0.5 x-2 > 6;
б)
![]() ; д)
x6
– 9 x3
+ 8 > 0;
; д)
x6
– 9 x3
+ 8 > 0;
в)
![]() ; е)
; е)
![]() .
.
