Подпрограммы

При решении сложных объемных задач часто целесообразно разбивать их на более простые подзадачи. Метод последовательной детализации позволяет составить программу из действий, которые сами представляют собой достаточно самостоятельные программы. В этом случае говорят о подпрограммах.

Подпрограмма – это часть программы, оформленная в виде отдельной синтаксической конструкции и снабженная именем.

Использование подпрограмм позволяет сделать основную программу более наглядной, понятной, а в случае, когда одна и та же последовательность команд встречается в программе несколько раз, даже более короткой и эффективной.

«Вызов» подпрограммы, то есть выполнение заданных в подпрограмме действий, может быть произведен в некоторой точке основной программы посредством указания имени подпрограммы.

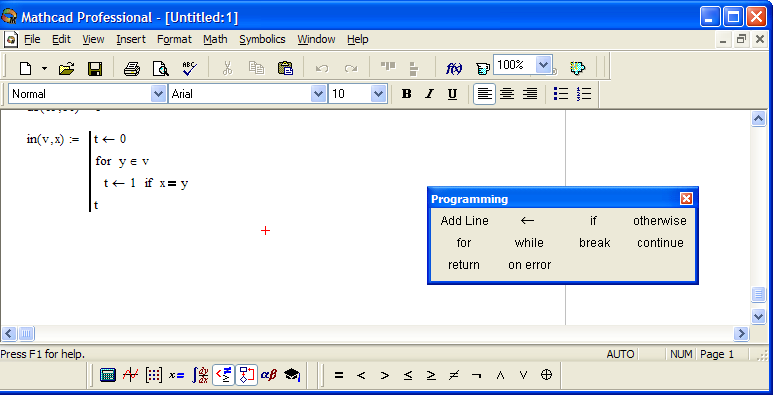
ПРИМЕР 9. Составить программу для нахождения общих элементов, содержащихся в двух заданных векторах. Эти векторы должны являться аргументами функции. Значением функции должен быть вектор, составленный из элементов, которые содержатся в первом и втором векторах.

Для решения этой задачи составить подпрограмму, определяющую, содержится ли число x в векторе v (1 - содержится, 0 - не содержится):

- пусть число в векторе не содержится - проверяем каждый элемент y вектора v - если элемент вектора = x, то t = 1 - возвращаем результат в основную программу

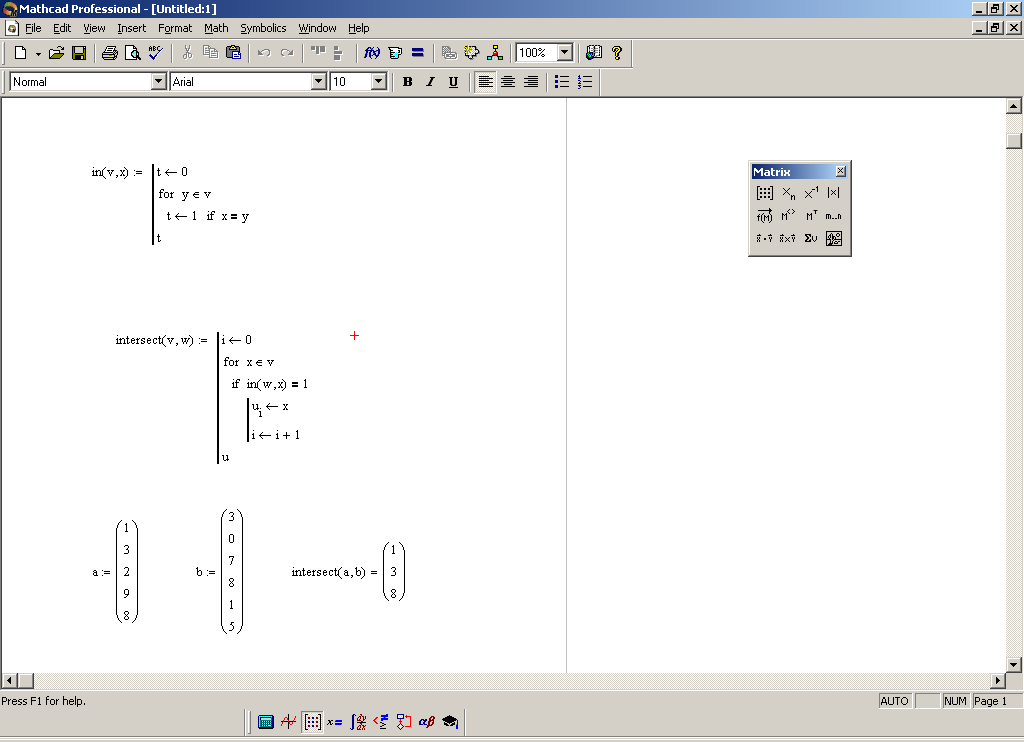
Основная программа сравнивает вектора v и w и возвращает вектор u, содержащий их общие элементы:

- № первого элемента вектора u - проверяем каждый элемент x вектора v - если x содержится в векторе w, то… - присвоить значение x элементу вектора u с номером i - увеличиваем порядковый номер на 1 - результат выполнения функции

Например, векторы 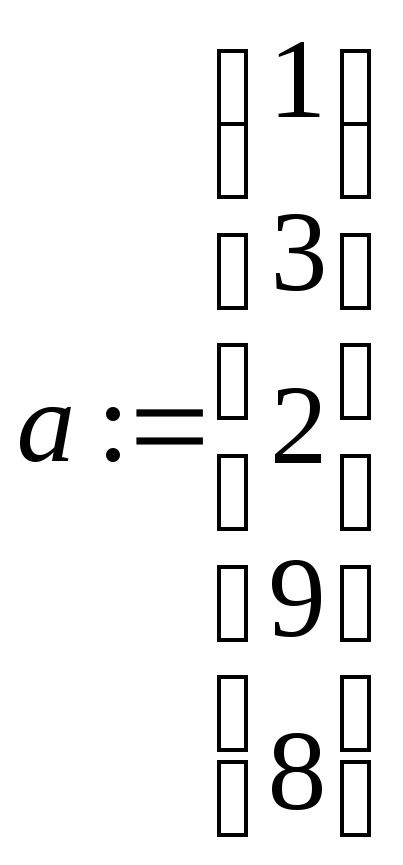и 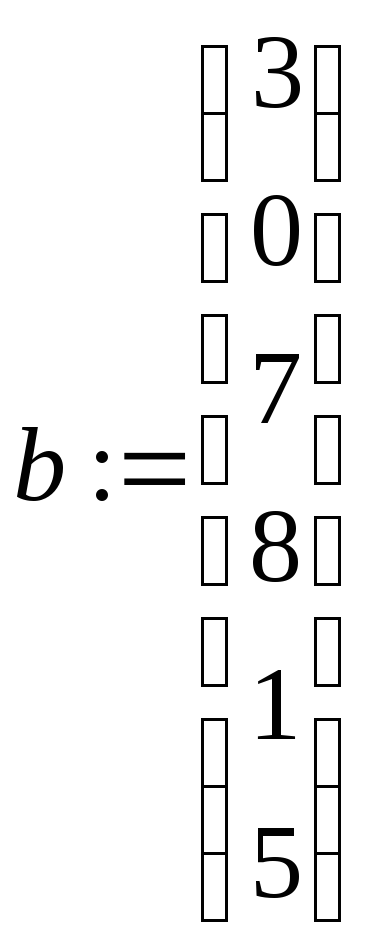имеют общие элементы .

ЗАДАНИЕ 25. Составить программу вычисления корней квадратного уравнения ax²+bx+c=0. В качестве исходных параметров берутся значения коэффициентов a, b, c. Если дискриминант меньше нуля, то значением функции должно быть число 1000, в противном случае значение функции - вектор, содержащий корни уравнения. Оформите вычисление корней в виде отдельной подпрограммы.

Задание 26. Составить функцию для вычисления суммы факториалов, оформив в виде подпрограммы нахождение факториала числа.

ЗАДАНИЕ 27. Вычислить max (min(3, 5), min(2, 6)).

ЗАДАНИЕ 28. Пусть процедура maxmin(x,y) присваивает параметру x большее из вещественных чисел x и y, а параметру y - меньшее. Описать данную процедуру и использовать ее для перераспределения значений вещественных переменных a, b и c так, чтобы стало a  b  c.

Задание 29. Найти все простые числа на заданном отрезке.

ЗАДАНИЕ 30. Вычислите

Контрольная работа №4

Вариант 1. Даны три числа a,b,c. Составить программу-функцию, реализующую следующий алгоритм. Если a  b  c, то все числа заменить их квадратами, если a>b>c, то каждое число заменить максимальным значением из этих трех чисел, в противном случае сменить знаки у чисел.

Вариант 2. Координаты точки на плоскости задаются двумя числами x,y. Составить программу-функцию, вычисляющую номер четверти на плоскости, в которую попала точка.

Вариант 3. Длина сторон треугольника задается числами a,b,c. Составить программу-функцию, вычисляющую значение целой переменной n по следующему правилу: n = 3, если три стороны равны; n = 2, если любые две стороны равны; n = 1, если все три стороны имеют разную длину.

Вариант 4. Подсчет числа элементов вектора, попадающих в интервал [a,b].

Вариант 5. Определение номера максимального элемента вектора.

Вариант 6. Дан вектор x, состоящий из n элементов. Составить программу-функцию, вычисляющую наибольшую из двух сумм элементов с четными и нечетными индексами.

Вариант 7. Определение числа положительных элементов матрицы.

Вариант 8. Перестановка местами максимального и минимального элемента матрицы.

Вариант 9. Дана матрица A размерности nm. Составить программу-функцию, формирующую вектор, i-й элемент которого равен среднему арифметическому i-й строки матрицы.

Вариант 10. Дана матрица A размерности nm. Составить программу-функцию, вычисляющую сумму и количество только тех элементов матрицы, которые удовлетворяют условию |A_i,j|  , где  - задаваемая величина.

Вариант 11. Даны две матрицы A,B размерности nm. Вычислить величину max=max A+max B, где max A, max B - максимальные значения матриц A,B соответственно. Для вычисления значения максимального элемента составить программу-функцию.

Вариант 12. Дана матрица A размерности nm. Составить программу-функцию, меняющую местами максимальный и минимальный элементы матрицы.

Вариант 13. Дана матрица A размерности nm. Составить программу-функцию, вычисляющую номер столбца, который содержит наименьший по модулю элемент этой матрицы.

Вариант 14.

Дан вектор x, состоящий из n элементов. Составить программу-функцию, вычисляющую среднее арифметическое элементов вектора, а затем преобразующую исходный вектор по правилу: те элементы, которые меньше среднего арифметического, заменить нулями.

Вариант 15. Имеется экзаменационная ведомость студенческой группы из n = 20 человек по m = 5 дисциплинам. Оценки из этой ведомости занесены в матрицу размерности nm. Составить программу-функцию, вычисляющую номер дисциплины (т.е. номер столбца), имеющей максимальный средний балл.

Вариант 16. Имеется экзаменационная ведомость студенческой группы из n = 15 человек по m = 4 дисциплинам. Оценки из этой ведомости занесены в матрицу размерности nm. Составить программу-функцию, вычисляющую номер студента (т.е. номер строки), имеющего максимальный средний балл по учебным дисциплинам.

Вариант 17. Имеется экзаменационная ведомость студенческой группы из n = 20 человек по m = 5 дисциплинам. Оценки из этой ведомости занесены в матрицу размерности nm. Составить программу-функцию, вычисляющую число студентов, получивших только четверки и пятерки.

Вариант 18. Имеется экзаменационная ведомость студенческой группы из n = 20 человек по m = 5 дисциплинам. Оценки из этой ведомости занесены в матрицу размерности nm. Составить программу-функцию, вычисляющую средний балл по каждой дисциплине.