Вычисление определенного интеграла

Чтобы вычислить определенный интеграл:

1. Щелкните в свободном месте документа и введите символ “&” или на панели Вычисления (Calculus) нажмите кнопку . Появится знак интеграла с пустыми полями для подынтегрального выражения, пределов интегрирования и переменной интегрирования.

2. Введите верхний и нижний пределы интегрирования в соответствующих местозаполнителях.

3. Введите в местозаполнитель между знаком интеграла и d выражение, которое нужно интегрировать.

4. В последний местозаполнитель введите имя переменной интегрирования.

5. Введите оператор численного <=> или символьного <> вывода для получения ответа.

Замечания:

• Пределы интегрирования должны быть вещественными. Выражение, которое нужно интегрировать, может быть вещественным либо комплексным.

• Кроме переменной интегрирования все переменные в подынтегральном выражении должны быть определены ранее в другом месте документа.

• Переменная интегрирования должна быть простой переменной без индекса.

• Если переменная интегрирования является размерной величиной, верхний и нижний пределы интегрирования должны иметь ту же самую размерность.

ЗАДАНИЕ 11. Вычислить, используя операторы численного интегрирования:

1. Интеграл функции Y=Sin⁴(x)·Cos(x) на интервале 0../4.

2. Ряд значений интеграла функции Y=Sin⁴(x)+Cos(x) на интервалах:

а) 0../8; б) 0../4; в) 0..3/8; г) 0../2.

Неопределенные интегралы

Чтобы вычислить неопределенный интеграл:

1. Щелкните в свободном месте документа и нажмите комбинацию клавиш <Ctrl>+<I> или кнопку на панелиВычисления (Calculus).

2. В первый местозаполнитель введите подынтегральное выражение, например, 2х²+y.

3. Введите переменную интегрирования в следующий местозаполнитель.

4. Введите оператор численного <=> или символьного <> вывода для получения ответа.

Если символьный процессор не может найти неопределенный интеграл, он возвращает интеграл неизменным.

ЗАДАНИЕ 12. Проверьте вычисление неопределенных интегралов:

1. x ² e ^x интегрирование дает x ²  exp ( x ) - 2 x exp ( x ) + 2 exp ( x )

2. интегрирование дает

ЗАДАНИЕ 13. Необходимо вычислить неопределенный интеграл от выражения 1/(3cos²(7-x))+x²/2. Выполните проверку, т.е. возьмите первую производную от результата и сравните ее значение с исходным выражением.

Пределы

В Mathcad есть три оператора вычисления пределов. Они могут быть вычислены только символьно.

Чтобы вычислить предел:

1. Щелкните в свободном месте документа.

2. Для вычисления предела нажмите комбинацию клавиш <Ctrl>+<L> или нажмите кнопку на панели Вычисления (Calculus). Чтобы вычислить левый предел, нажмите <Ctrl>+<Shift>+<B> или кнопку панели. Для вычисления правого предела нажмите <Ctrl> +<Shift>+<A> или кнопку панели.

2. Введите выражение в поле ввода справа от оператора.

3. Введите в левый местозаполнитель внизу оператора переменную, по которой вычисляется предел.

4. Введите в правый местозаполнитель внизу оператора значение предела.

5. Введите оператор численного <=> или символьного <> вывода для получения ответа. Если предел не существует, Mathcad возвратит сообщение "Неопределено".

ЗАДАНИЕ 14. Проверьте нахождение пределов:

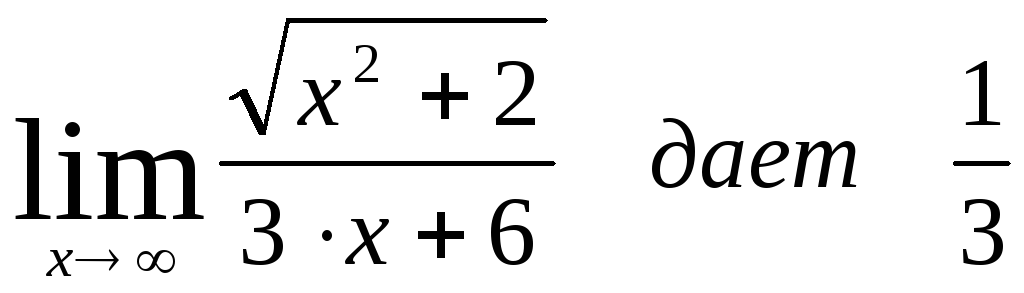
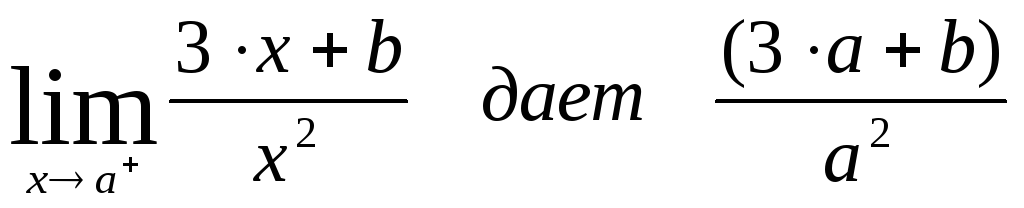
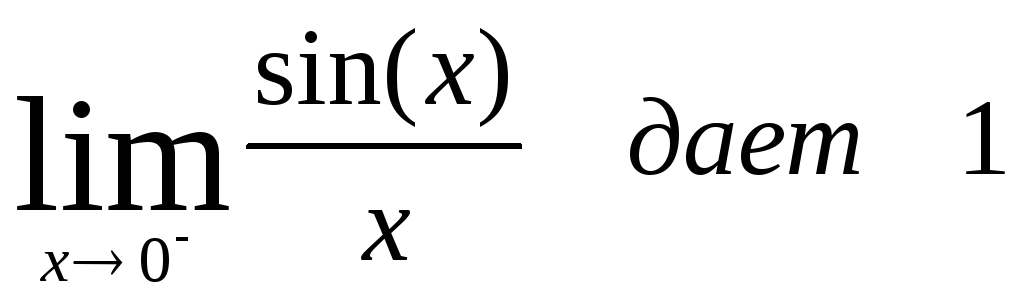
ЗАДАНИЕ 15. Вычислите предел:

1. Дроби, числитель которой равен 2ⁿ+3ⁿ+4ⁿ, а знаменатель 4ⁿ⁺¹+3, при n, стремящемся к бесконечности.

2. Определить, является ли непрерывной в точке x=5 функция, заданная следующим образом:

Замечание. Вычислите пределы, стремящиеся справа и слева к x=5, и сравните их. Также вычислите значение функции при x=5. Если все эти значения равны, то функция непрерывна в этой точке.