Матричный способ решения систем уравнений

Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных х₁, х₂, …, х_n:

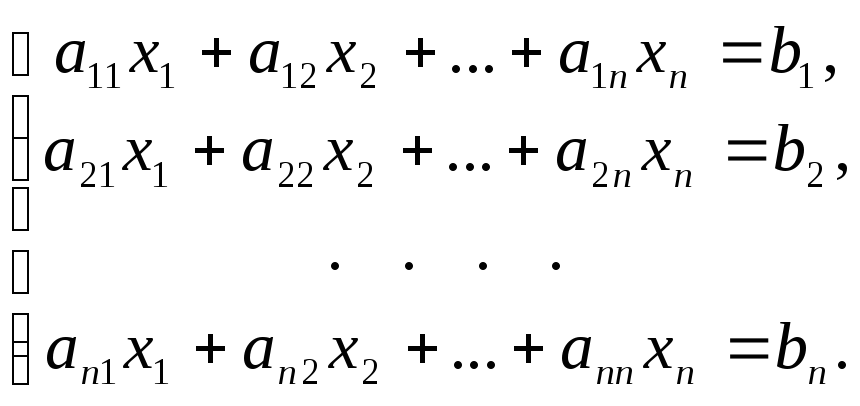(1)

В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричном виде Ах=b (2), где

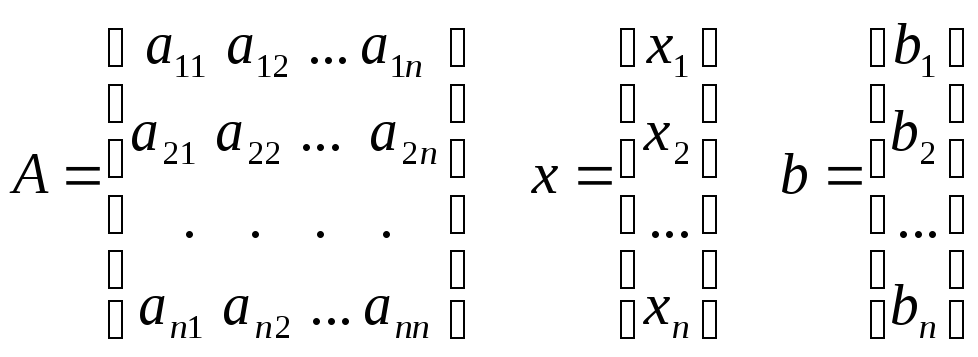. (3)

Матрица А, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении, называется матрицей системы. Матрица-столбец b, элементами которой являются правые части уравнений системы, называется матрицей правой части или просто правой частью системы. Матрица-столбец х, элементы которой - искомые неизвестные, называется решением системы.

Если определитель матрицы А не равен 0, то система (1, или эквивалентное ей матричное уравнение (2) имеет единственное решение.

Системы линейных уравнений удобно решать с помощью функции lsolve(Ax,b), возвращающей вектор решения x такой, что Ах = b.

ПРИМЕР 7. Решим матричным способом систему уравнений

3x₁ – x₂ = 5;

-2x₁ + x₂ + x₃ = 0;

2x₁ – x₂ + 4x₃ = 15.

_{1. Формируем матрицу А и вектор b: .}

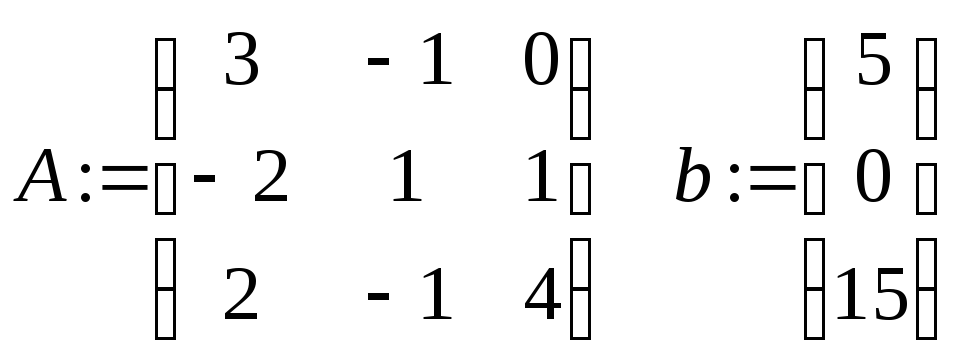2. Вычисляем определитель: |A| = 5. Определитель отличен от нуля, значит, система имеет единственное решение.

3. Решаем систему с помощью функции lsolve: x:=lsolve(A, b).

4. Выводим решение, набрав х=.

5. Проверяем правильность решения, набрав Ax – b =. Должен получиться нулевой вектор.

Приближенные решения

Иногда при попытке найти решение уравнения или системы уравнений с помощью функции Find выдается сообщение об ошибке "Решение не найдено" (“No solution was found”). Это сообщение появляется, когда различие между текущим приближением и приближением, полученным на предыдущем шаге итераций, больше, чем значение встроенной переменной TOL.

Если при поиске решения встречаются трудности, то полезно вывести те или иные графики, связанные с системой. Анализ графика может облегчить поиск области, в которой может находиться искомое решение. Это поможет выбрать подходящее начальное приближение.

Mathcad содержит функцию, очень похожую на функцию Find. Функция Minerr использует тот же самый алгоритм, что и функция Find. Различие состоит в следующем. Если в результате поиска решения не может быть получено дальнейшее уточнение текущего приближения к решению, Minerr возвращает это приближение. Функция Find в отличие от функции Minerr возвращает в этом случае сообщение об ошибке «Решение не найдено». Правила использования функции Minerr такие же, как и функции Find.

ПРИМЕР 8. Решить систему уравнений 2x-6=0 и 2-x=0.

1. Задайте начальные значения переменной: x:=1.

2. Напишите слово Given, после которого в следующих строках запишите уравнения системы.

3. В следующей строке наберите Minerr (x)=.

Символьное решение уравнений

Имеются некоторые задачи, для которых возможности Mathcad позволяют находить решения в символьном (аналитическом) виде. Решение уравнений в символьном виде позволяет найти точные или приближенные корни уравнения:

• если решаемое уравнение имеет параметр, то решение в символьном виде может выразить искомый корень непосредственно через параметр. Поэтому вместо того, чтобы решать уравнение для каждого нового значения параметра, можно просто заменять его значение в найденном символьном решении;

• если нужно найти все комплексные корни полинома со степенью меньше или равной 4, символьное решение даст их точные значения в одном векторе либо в аналитическом, либо в цифровом виде.

Команда Символы (Symbolics) \ Переменные (Variable) \ Вычислить (Solve) позволяет решить уравнение относительно некоторой переменной и выразить его корни через остальные параметры уравнения.

Для решения уравнения в символьном виде:

1. Ввести выражение.

2. Щелкнув мышью, выделить переменную, относительно которой нужно решить уравнение, приравнивающее выражение нулю.

3. Выбрать пункт меню Символы (Symbolics) \ Переменные (Variable) \ Вычислить (Solve).

ПРИМЕР 9. Решим в символьном виде уравнение Ax²+Bx+C=0.

1. Введите выражение a∙x²+b∙x+c.

2. Щелчком мыши выделите переменную х.

3. В меню Символы (Symbolics) выберите команду Переменные (Variable) \ Вычислить (Solve). Mathcad выведет корни уравнения, выраженные через переменные А, В и С.

Можно также решать неравенства, использующие символы <, >,  и . Решения для неравенств будут отображаться в терминах булевых выражений Mathcad.

Чтобы решить систему уравнений в символьном виде:

1. Напечатать ключевое слово Given.

2. Напечатать уравнения в любом порядке ниже слова Given. Удостоверьтесь, что для ввода знака “=” используется <Ctrl>+<=>.

3. Напечатать функцию Find, соответствующую системе уравнений.

4. Нажать <Ctrl>+<.> (клавиша <Ctrl>, сопровождаемая точкой). Mathcad отобразит символьный знак равенства “”.

5. Щелкнуть мышью на функции Find.

ПРИМЕР 10. Решить в символьном виде систему уравнений: