Лабораторная работа № 6 Решение уравнений Решение уравнения с одним неизвестным

Для решения одного уравнения с одним неизвестным f(x)=0 используется функция root, возвращающая значение переменной, обращающее выражение в ноль. В зависимости от типа задачи данная функция может включать либо два, либо четыре аргумента и, соответственно, работает несколько по-разному.

• root(f(х),х)

• root(f(х),х,a,b),

где f(х) - функция, определяющая уравнение; х - переменная, относительно которой решается уравнение; a,b – границы интервала, внутри которого происходит поиск корня.

Первый тип функции root требует дополнительного задания начального значения переменной х. Для этого нужно просто предварительно присвоить х некоторое число. Поиск корня будет производиться вблизи этого числа.

ПРИМЕР 1. Найдем решение уравнения x³ = e^x.

1. Определите выражение, которое должно быть обращено в ноль. Для этого преобразуйте уравнение x³=e^x к виду x³-e^x=0. Левая часть этого выражения и является первым аргументом функции root.

2. Для определения начального приближения постройте график функции f(х)=x³-e^x и с помощью трассировки найдите его пересечение с осью ОХ.

3. Определите начальное значение переменной x: введите x:=1.855 (рис.20).

4. Определите переменную a как корень уравнения. Для этого введите a:=root(x³-e^x, x).

5. Напечатайте a=, чтобы увидеть значение корня.

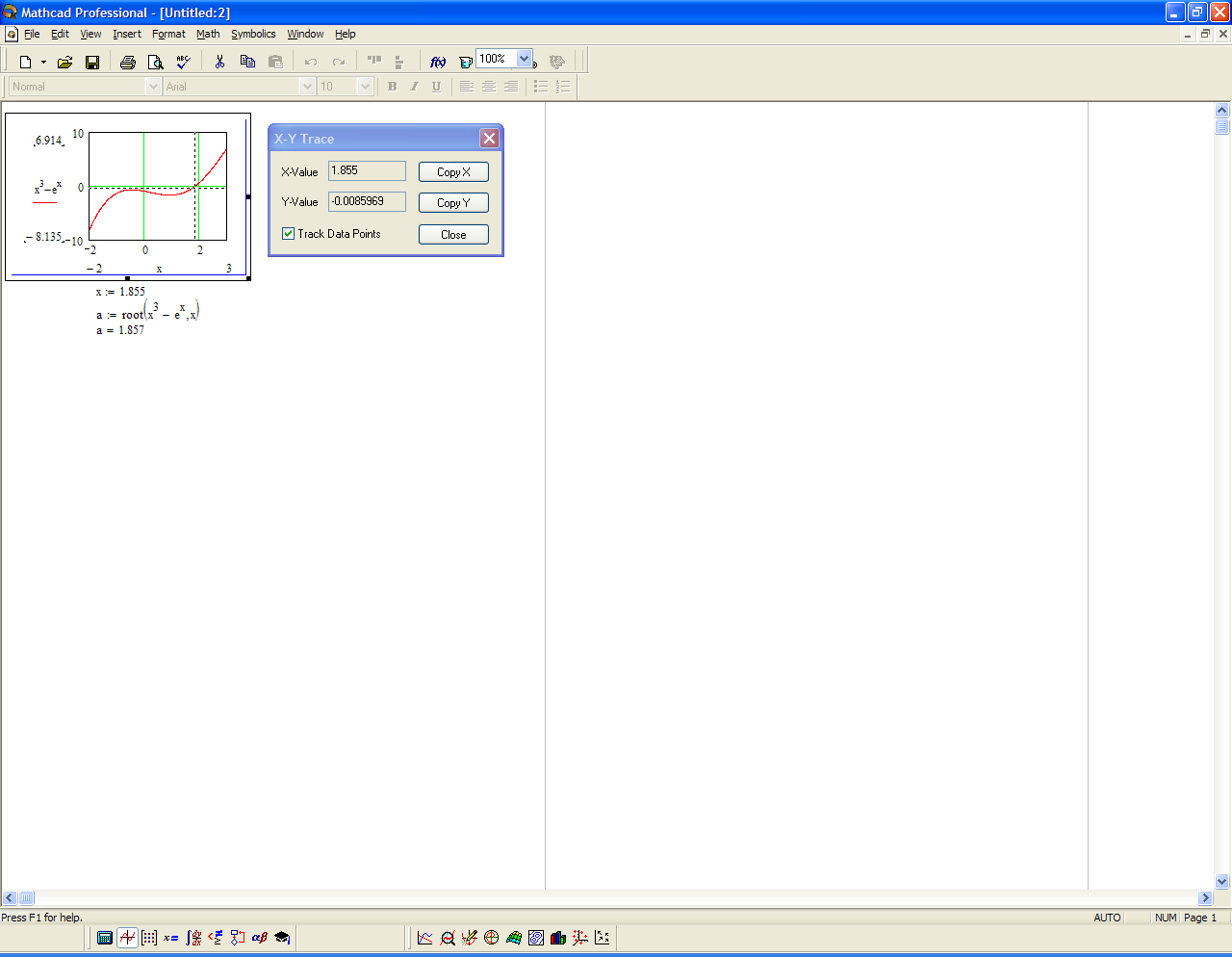
Рис. 20. Использование функции root(f(x),x) для решения уравнения x³=e^x

Иногда удобнее задавать не начальное приближение к корню, а интервал [a,b], внутри которого корень заведомо находится. В этом случае следует использовать функцию root с четырьмя аргументами, а присваивать начальное значение х не нужно.

ПРИМЕР 2. Найдем решение уравнения x³ = e^x, используя вторую разновидность функции root.

1. Используя построенный ранее график функции f(x), в качестве интервала [a,b] возьмем отрезок [1,3].

2. Определите переменную с как корень уравнения, введя c:=root(x³-e^x,x,1,3).

3. Напечатайте c=, чтобы увидеть значение корня.

Замечание. Когда root имеет четыре аргумента, следует помнить о двух ее особенностях:

• внутри интервала [a,b] не должно находиться более одного корня, иначе будет найден только один из них, заранее неизвестно какой именно;

• значения f(a) и f(b) должны иметь разный знак, иначе будет выдано сообщение об ошибке.

Если Mathcad не может найти подходящего приближения, то появляется сообщение об ошибке "Отсутствует сходимость". Эта ошибка может быть вызвана следующими причинами:

• уравнение не имеет корней;

• корни уравнения расположены далеко от начального приближения;

• выражение имеет локальные максимумы или минимумы между начальным приближением и корнями.

• выражение имеет разрывы между начальным приближением и корнями.

Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значение. Чем точнее выбрано начальное приближение корня, тем быстрее функция root сходиться к точному значению.

Точность вычислений определяется системной переменной TOL, равной по умолчанию 10^-3. Для изменения точности, с которой функция root ищет корень, можно изменить значение встроенной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, функция root будет медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, использует определение вида TOL:=0.01.