Трассировка и масштабирование

Трассировка позволяет очень точно изучить строение графика. Для того чтобы включить режим трассировки, щелкните в области графика правой кнопкой мыши и выберите в контекстном меню пункт Трассировка (Trace) либо выделите график и выберите в меню Формат (Format) команду График (Graph) \ Трассировка (Trace).

В результате появится окно трассировки (рис. 14), а после щелчка в поле графика вы увидите две пересекающиеся пунктирные линии.

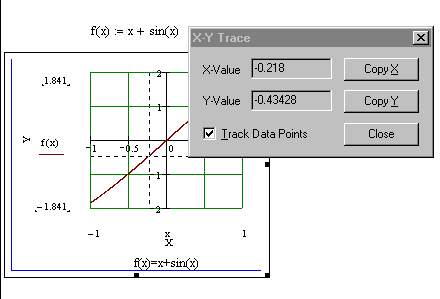
Рис. 14. Трассировка графика

Перемещая указатель мыши по графику, вы тем самым передвигаете точку пересечения линий трассировки. При этом координаты точки указываются с высокой точностью в окне трассировки в полях Значение Х (X-Value) и ЗначениеY (Y-Value). Нажатие кнопки Копировать Х (Copy X) или Копировать Y (Copy Y) копирует соответствующее число в буфер обмена. В дальнейшем его можно вставить в любое место документа.

Если установлен флажок Следовать за рядом данных (Track Data Points), как это показано на рис.14, то линии трассировки следуют точно вдоль линии графика. В противном случае они могут перемещаться по всей области графика.

Еще одно средство для работы с двухмерными графиками заключается в просмотре графика в увеличенном масштабе. Для вызова окна диалога выберите в контекстном меню или в меню Формат (Format) пункты График (Graph) и Масштаб (Zoom). После этого указателем мыши выделите прямоугольную область на графике, которую вы хотите просмотреть в увеличенном масштабе (рис. 15), и нажмите кнопку Увеличить (Zoom). В результате часть графика будет прорисовываться более крупно.

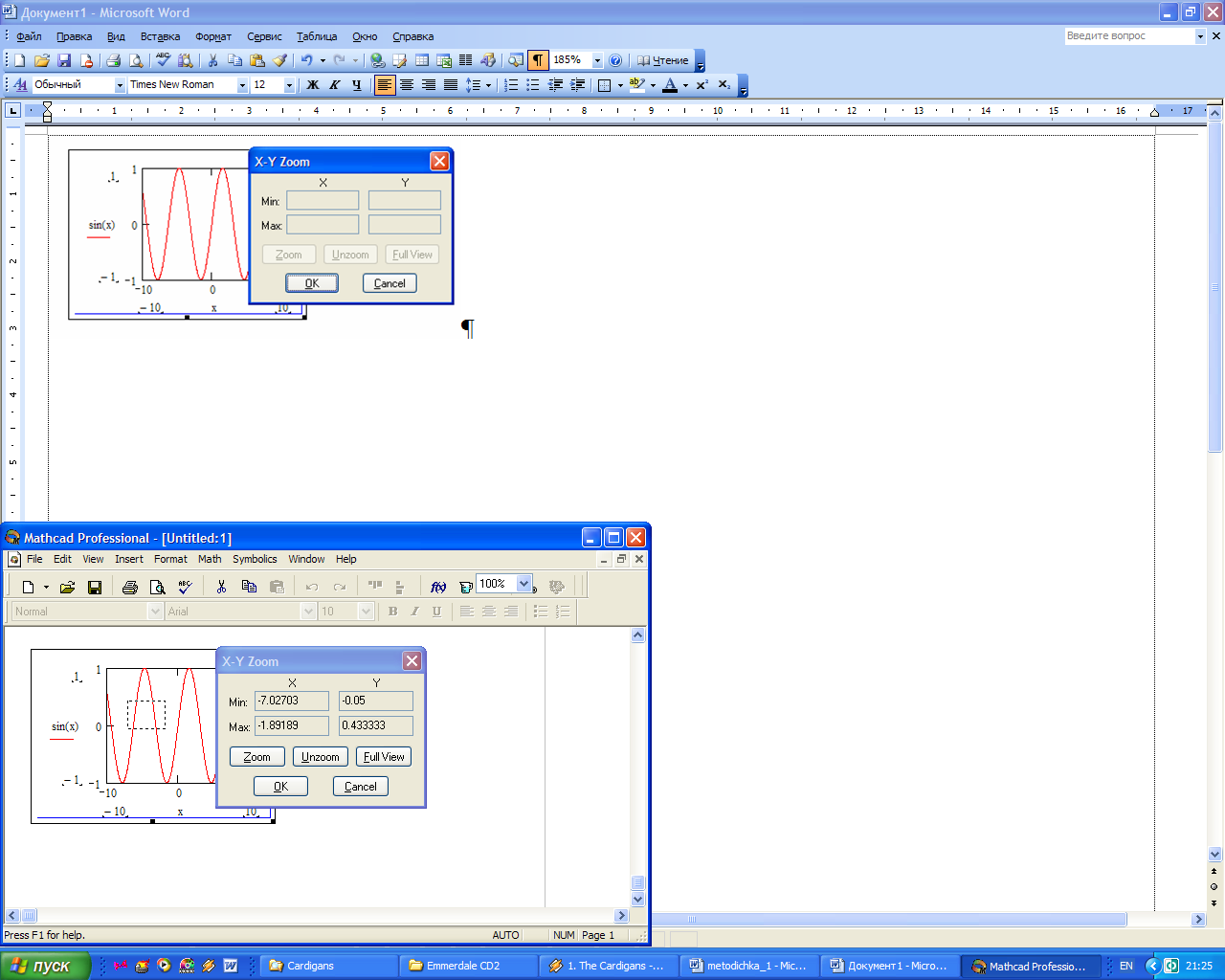
Рис. 15. Масштабирование графика

Далее можно продолжать изменять масштаб, вернуться к прежнему виду графика кнопкой Показать целиком (Full View) либо закрыть окно диалога для окончательной перерисовки графика в крупном масштабе (нажав кнопку ОК).

Графики в полярной системе координат

В полярной системе координат каждая точка задается углом fi и модулем радиус-вектора r(fi). График функции обычно строится в виде линии, которую описывает конец радиус-вектора при изменении угла fi в определенных пределах, чаще всего от 0 до 2.

Чтобы создать график в полярных координатах:

1. Определите приращение для угла. Например, N:=50.

2. Определите угол как дискретный аргумент с заданным приращением. Например, fi:=0,2*/N…2*.

3. Определите радиус как функцию от угла. Например, r(fi):=cos(fi)+1.

4. Щелкните мышью там, где нужно создать график.

5. Выберите в меню Вставка (Insert) пункт Графики (Graph) \ Полярные координаты (Polar Plot). Появится круг с четырьмя полями ввода.

6. В поле ввода внизу введите угловую переменную графика или любое выражение, включающее эту переменную. Например, fi.

7. В поле ввода слева должно содержать выражение для радиуса. Например, r(fi).

8. Два поля ввода справа предназначены для верхнего и нижнего граничных значений радиуса. Mathcad заполняет эти поля автоматически.

9. Нажмите <F9>, чтобы увидеть график.

Форматирование графика в полярной системе координат во многом совпадает с форматированием графика в декартовой системе координат.

Можно построить несколько графиков на одном и том же чертеже в полярных координатах, также как и при построении графиков в декартовых координатах.

ЗАДАНИЕ 3. Построить график зависимости R(fi)=acos(mfi) для fi=-.. с шагом /120 со следующими значениями параметров: a=3, m=2, m=3, m=4.

ЗАДАНИЕ 4. Постройте кривые, заданные в полярной системе координат. Коэффициенты a и b выберите самостоятельно. Для каждой кривой постройте первый график, используя установки формата по умолчанию, а затем постройте второй график, в котором измените установки для осей координат и свойства графика.

№ пп	Уравнение кривой r=f(fi)	Название кривой	№ пп	Уравнение кривой r=f(fi)	Название кривой
1	r=a*cos(4*fi)	роза	7	r=a*sin(fi/3)	роза
2	r=a*fi	спираль Архимеда	8	r=a*sin(4*fi/3)	роза
3	r=a*fi2	спираль Галилея	9	r=a*sin(fi/2)	роза
4	r2=a2*fi	спираль Ферма	10	r=a*sin(5*fi/3)	роза
5	r=a*sin(3*fi)	четырехлепестковая роза	11	r=2*a*sin2(fi)/cos(fi)	циссоида
6	r=a*sin(2*fi)	трехлепестковая роза	12	r=a*cos(fi)+b	улитка Паскаля