Создание массива путем определения его элементов

Можно присвоить значения непосредственно отдельным элементам массива. В этом случае создается массив, размерность которого задается индексами введенного элемента, а неопределенным элементам по умолчанию присваиваются нулевые значения.

ПРИМЕР 1.

1. Задайте элемент матрицы, последовательно введя Q[3,2:7.

2. Затем наберите Q=. В результате получите матрицу как на рис.8.

Аналогичным образом можно создать и вектор (см. рис. 8).

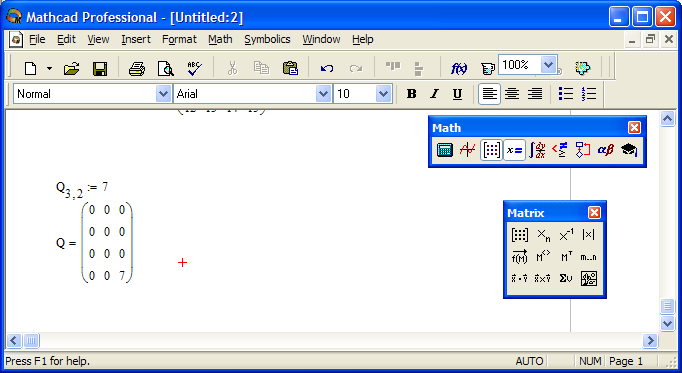
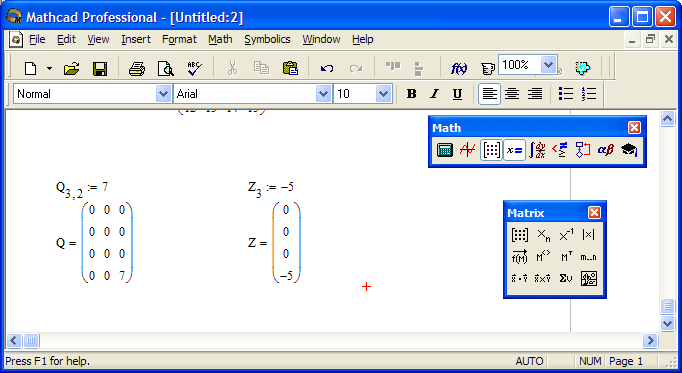
Рис.8. Создание матрицы и вектора определением одного элемента

Создание матрицы с помощью дискретных аргументов

В Mathcad можно определить переменную как вектор, значения элементов которого подчиняются арифметической прогрессии, т.е. каждый последующий элемент на постоянную величину (шаг) больше предыдущего.

Для определения такого вектора нужно:

1. Щёлкнуть в свободном месте документа.

2. Набрать имя вектора и оператор присваивания “:=”.

3. Набрать значение первого элемента вектора, а затем через запятую значение второго элемента.

4. Набрать символ ";" и значение последнего элемента вектора.

5.Для проверки результата определения вектора наберите имя вектора и “=”.

Например, U:=5,7..73 - задан вектор U, первый элемент которого равен 5, а каждый последующий увеличивается на 2.

ПРИМЕР 2. Рассмотрим еще один способ определения массива, в котором значения каждого из его элементов функционально зависят от значений индексов. Определите переменные j и k как целочисленные дискретные аргументы (используем их в дальнейшем как индексы массива R):

j:=0..3 k:=0..4 R_j,k:=k+j

Для проверки результата наберите R=.

ЗАДАНИЕ 4.

1. Определите векторы F, G и H как соответственно 1-й, 3-й и 8-й столбцы матрицы R (из примера 2). Выведите значения этих векторов.

2. Сформируйте векторы S, C, S2 и C2, элементы которых содержат значения функций соответственно Sin X, Cоs  X, Sin²  X и Сos²  X, где Х - дискретно заданный угол (в градусах) в диапазоне от 0 до 360 с шагом 10.

Векторные и матричные операторы

Многие из этих операторов доступны из палитры символов. Обратите внимание, что операторы, которые ожидают в качестве аргумента вектор, всегда ожидают вектор-столбец, а не вектор-строку. Чтобы заменить вектор-строку на вектор-столбец, используйте оператор транспонирования.

В таблице приняты обозначения:

• А и В - массивы (векторы или матрицы).

• u и v - векторы.

• М и N - квадратные матрицы.

• u_i и v_i - отдельные элементы векторов u и v.

• z - скаляр.

• m, n, i, j - целые числа.

Операция	Обознач.	Клавиши	Описание
Умножение матрицы на скаляр	A*z	*	Умножает каждый элемент А на скаляр z
Скалярное произведение	u*v	*	Возвращает скаляр: ui*vi.Векторы должны иметь одинаковое число элементов.
Матричное умножение	А*В	*	Возвращает произведение матриц А и В, число столбцов в А должно соответствовать числу строк в В.
Умножение матрицы на вектор	А*v	*	Возвращает произведение матриц А и v, число столбцов в А должно соответствовать числу строк вv.
Деление	А/z	/	Делит каждый элемент массива на скаляр.
Сложение векторов и матриц	А+В	+	Складывает соответствующие элементы А и В, массивы должны иметь одинаковое число строк и столбцов.
Скалярная сумма	А+z	+	Добавляет скаляр zк каждому элементу А.
Векторное и матричное вычитание	А-В	-	Вычитает соответствующие элементы А из элементов массива В, массивы должны иметь одинаковое число строк и столбцов.
Скалярное вычитание	А - z	-	Вычитает скаляр из каждого элемента А.
Изменение знака	- А	-	Умножает все элементы А на –1.

Операция	Обознач.	Клавиши	Описание
Степени матрицы, обращение матриц	М n	^	n-я степень квадратной матрицы М (использует умножение матриц).N– целое число. М–1матрица,обратнаяк М. Другие отрицательные степени – степени обратной матрицы. Возвращает матрицу.
Длина вектора	|v|	|	Возвращает длину вектора
Детерминант (определитель)	|M|	|	Возвращает детерминант квадратной матрицы М, результат – скаляр.
Транспонирование	А Т	<Ctrl>+1	Возвращает матрицу, делая столбцы исходной матрицы строками, а строки - столбцами.
Векторное произведение	u x v	<Ctrl>+8	Возвращает векторное произведение для векторов с тремя элементами.
Суммирование элементов	v	<Ctrl>+4	Суммирует элементы вектора и возвращает скаляр.
Верхний индекс	A<n>	<Ctrl>+6	Извлекает n-й столбец массива A. Возвращает вектор.
Нижний индекс (вектора)	vn	[	Возвращает n-й элемент вектора
Нижние индексы матрицы	Am,n	[	Возвращает элемент матрицы, находящийся в m-м  ряду и n-й строке