Исследуем общее уравнение.

1) – прямая проходит через начало координат;

2) – прямая параллельна оси ;

а) , ось – уравнение оси ;

3) – прямая параллельна оси ;

а) , - уравнение оси .

д) Уравнение прямой в “отрезках” на осях.

Рассмотрим общее уравнение прямой в предположении, что ни один из коэффициентов не равен 0.

.

Оно может быть приведено к специальному виду, удобному при решении задач. Перенесем в другую часть уравнения

.

Разделим на

или .

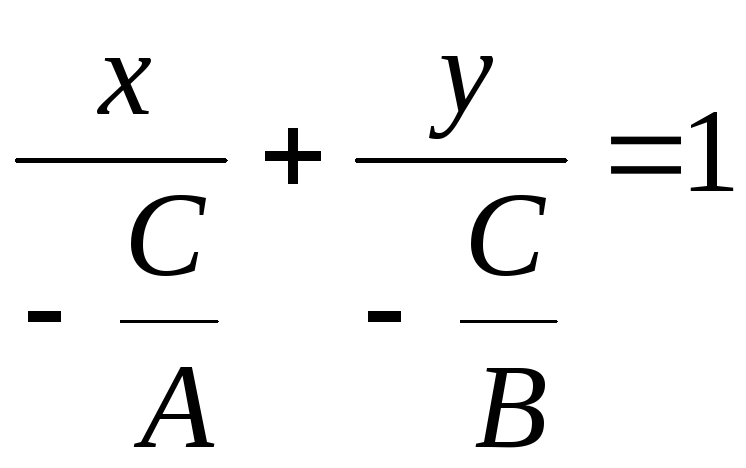Обозначим , тогда

Получено уравнение “в отрезках” на осях: – величина отрезка, отсекаемого прямой на оси , – на оси .

е) Нормальное уравнение прямой.

Этот вид уравнения получил свое название из-за нормали (перпендикуляра, проведенного из начала координат на прямую) (рис. 18).

0

Рис. 18.

Обозначим – расстояние от начала координат до прямой, – угол нормали к оси , - текущая точка – .

Из : , – угол с .

Из : , преобразовав, получим:

,

.

– нормальное уравнение.

Главная особенность этого уравнения – сумма квадратов коэффициентов при неизвестных равна единице.

Замечание. Чтобы общее уравнение прямой преобразовать к нормальному виду, его необходимо умножить на нормирующий множитель.

.

Знак берется противоположным свободному члену.

Например:

.

Следствие. Расстояние от точки до прямой

• если прямая задана нормальным уравнением:

и точка , то расстояние точки А до прямой выразится так:

;

• если прямая задана в общем виде, то

.

Пример 25. В треугольнике заданы вершины: , , . Найти длину и уравнение стороны ; длину и уравнение медианы , точку пересечения медиан ; длину и уравнение высоты .

Решение.

Схематично изобразим треугольник:

а) длину стороны найдем по формуле .

б) Уравнение стороны составим, используя уравнение прямой, проходящей через две точки

,

,

– уравнение стороны

в) Найдем точку – середину .

, , , .

г) Уравнение медианы находим аналогично уравнению .

– уравнение медианы .

д) Найдем точку – она делит медиану в отношении 2:1, т.е. .

.

е) Высота перпендикулярна прямой – значит, их угловые коэффициенты удовлетворяют условию

, .

Уравнение составим на основе уравнения пучка прямых – ведь нам известна точка и угловой коэффициент .

,

– уравнение высоты .

ж) Длину высоты определим как расстояние от вершины до прямой , представленной в общем виде:

–длина высоты .

Пример 26. Даны две стороны параллелограмма 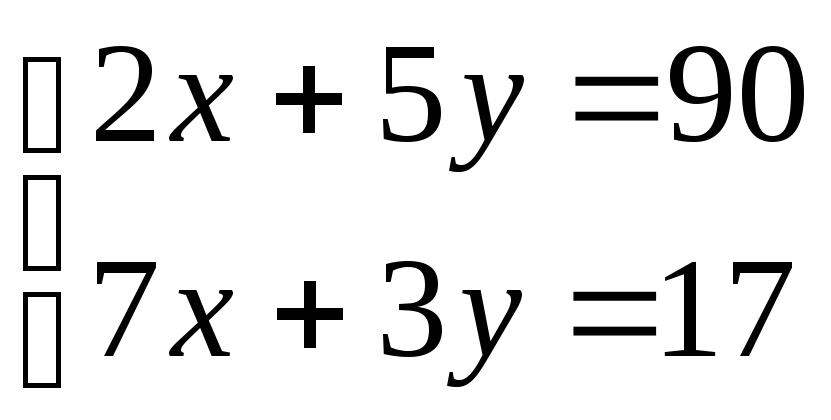и точка пересечения диагоналей .

Найти уравнения двух других сторон.

Решение.

										В условии даны уравнения смежных сторон (т.к. они не параллельны). Предположим, что это стороны и .

а) Определим вершину как пересечение сторон

.

б) Найдем вершину , зная, что – середина

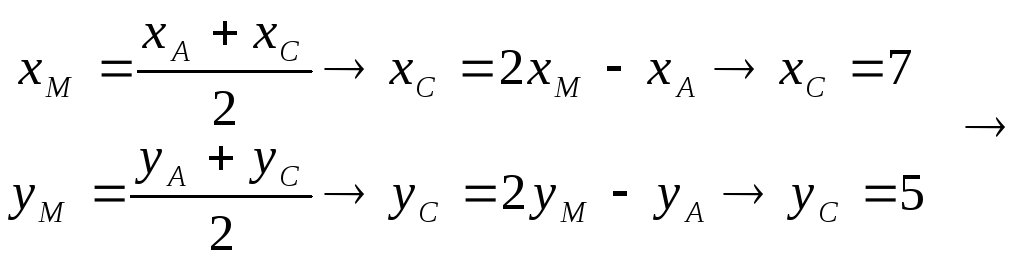
в) Уравнение параллельно и проходит через точку

.

Уравнения искомых сторон:

и

и

и

Задания для индивидуального решения