
- •Экономики и торговли
- •Ббк 22.1я 73
- •ВВедение
- •Определители и системы линейных уравнений
- •1.2. Системы трех линейных уравнений и определители третьего порядка
- •2.1. Понятие о матрицах Матрицейназывается прямоугольная таблица чисел следующего вида:
- •2.2. Действия над матрицами
- •2.3. Решение систем линейных уравнений методом обратной матрицы
- •2.4. Метод Гаусса для решения систем линейных уравнений
- •3. Вопросы совместимости линейных уравнений
- •3.1. Ранг матрицы Рангом матрицы называется наивысший порядок отличного от нуля определителя, который можно образовать из элементов данной матрицы, сохраняя порядок следования элементов.
- •3.2. Системы линейных неоднородных уравнений
- •3.3. Системы линейных однородных уравнений
- •4. Элементы векторной алгебры и метода координат
- •4.1. Векторные величины и действия над ними
- •Исследуем общее уравнение.
- •Часть I. Определители, Матрицы,
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Часть II. Векторы
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Часть III. Прямая линия на плоскости
- •Литература
Вариант 12
Найти координаты вектора
 ,
если
,
если
 .
.а) (0; 13);
б) (6; -1);
в) (12; -1);
г) другой ответ.
Даны векторы
 ,
, .
При каком значении
.
При каком значении
 эти векторы перпендикулярны?
эти векторы перпендикулярны?а)
 ;
;б)
 ;
;в) 9;
г) другой ответ.
Найти вектор
 ,
коллинеарный вектору
,
коллинеарный вектору и удовлетворяющий условию
и удовлетворяющий условию .
.
|
а) (-2; -5; 1); |
б) (-4; -10; 2); |
в) (4; 5; 2); |
г) другой ответ. |
Найти направляющие косинусы вектора
 .
.
|
а)
|
б)
|
в)
|
г) другой ответ. |
Какой угол образуют единичные векторы
 и
и
 ,
если векторы
,
если векторы
 и
и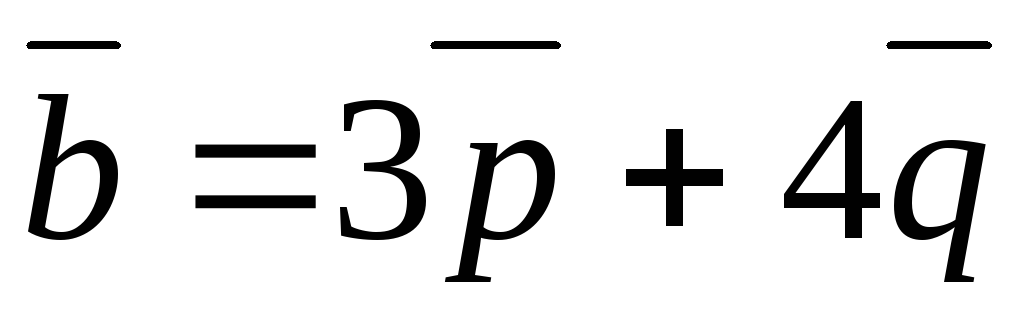 взаимно перпендикулярны?
взаимно перпендикулярны?а) другой ответ;
б)
 ;
;в)
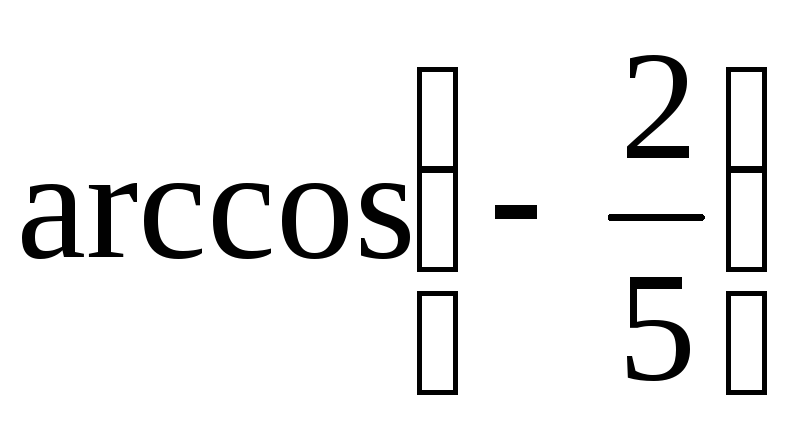 ;
;г)
 .
.Даны две точки
 ,
, .
Точка
.
Точка делит отрезок
делит отрезок
 в отношении
в отношении .
Найти координаты точки
.
Найти координаты точки .
.а)
 ;
;б)
 ;
;в)
 ;
;г) другой ответ.
На плоскости даны точки
 ,
, ,
, .
В начале координат приложены силы
.
В начале координат приложены силы ,
, и
и .
Найти проекцию вектора
.
Найти проекцию вектора на равнодействующую сил
на равнодействующую сил .
.а)
 ;
;б)
 ;
;в) другой ответ;
г)
 .
.Показать, что векторы
 ,
, ,
, образуют трехмерный базис и представить
вектор
образуют трехмерный базис и представить
вектор в этом базисе.
в этом базисе.
|
а)
|
б)
|
в) другой ответ; |
г)
|
Вариант 13
Найти координаты вектора
 ,
если
,
если
 .
.а) (-4; - 7);
б) (5; 6);
в) (-13; -18);
г) другой ответ.
Даны векторы
 ,
, .
При каком значении
.
При каком значении эти векторы перпендикулярны?
эти векторы перпендикулярны?а)
 ;
;б) -15;
в) 3;
г) другой ответ.
Найти вектор
 ,
коллинеарный вектору
,
коллинеарный вектору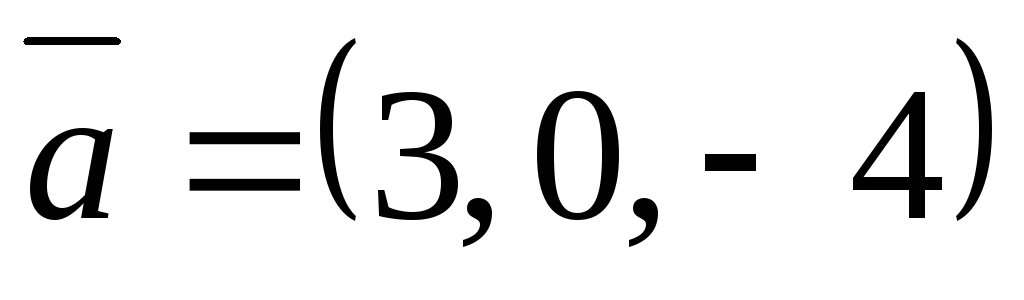 и удовлетворяющий условию
и удовлетворяющий условию .
.а) (-3;0;4);
б) (6;0;-8);
в) другой ответ;
г) (-6; 5; 8).
Найти направляющие косинусы вектора
 .
.а)
 ;
;б)
 ;
;в)
 ;
;г) другой ответ.
Какой угол образуют единичные векторы
 и
и
 ,
если векторы
,
если векторы
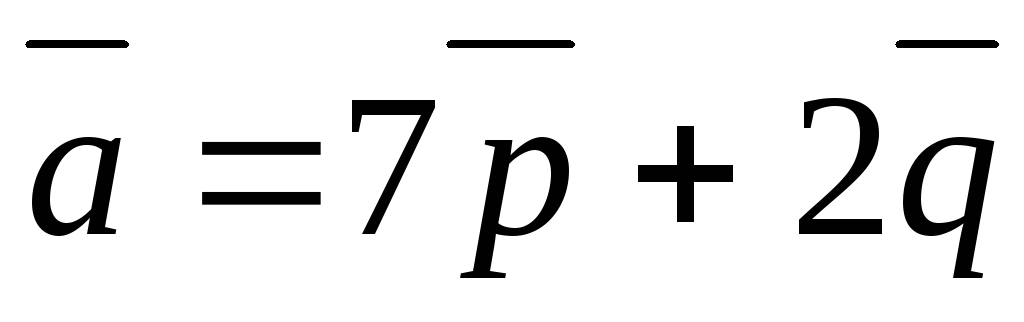 и
и взаимно перпендикулярны?
взаимно перпендикулярны?а)
 ;
;б) другой ответ;
в)
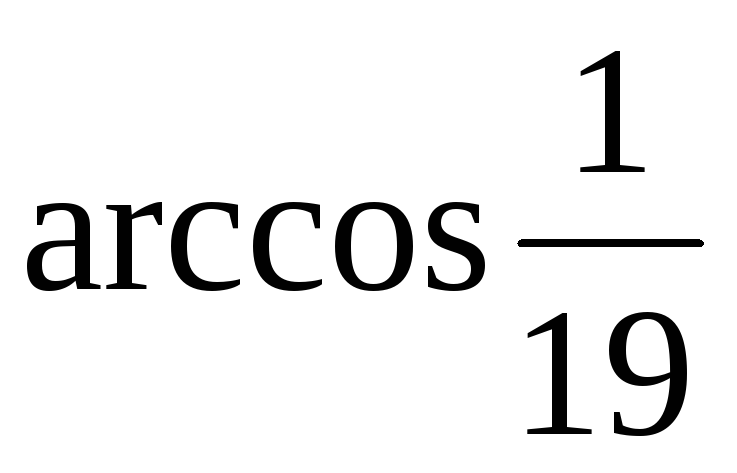 ;
;г)
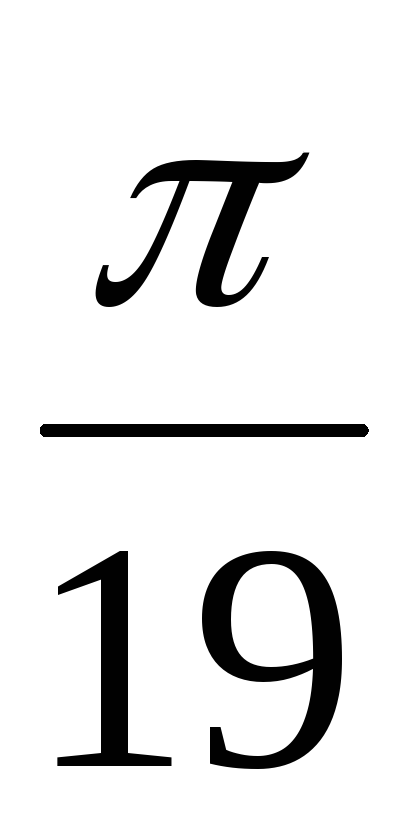 .
.Даны две точки
 ,
, .
Точка
.
Точка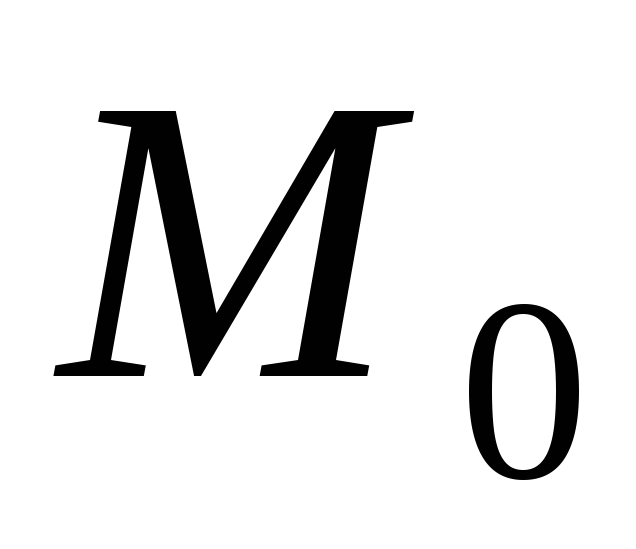 делит отрезок
делит отрезок
 в отношении
в отношении .
Найти координаты точки
.
Найти координаты точки .
.а)
 ;
;б)
 ;
;в)
 ;
;г) другой ответ.
На плоскости даны точки
 ,
, ,
, .
В начале координат приложены силы
.
В начале координат приложены силы ,
, и
и .
Найти проекцию вектора
.
Найти проекцию вектора на равнодействующую сил
на равнодействующую сил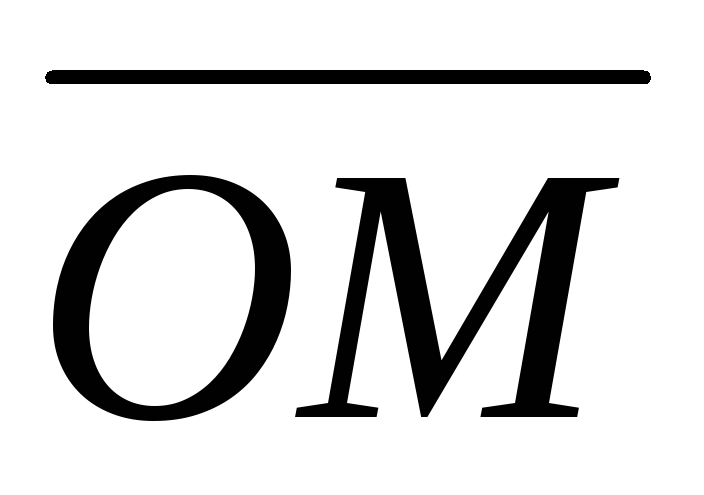 .
.а)
 ;
;б)
 ;
;в)
 ;
;г) другой ответ.
Показать, что векторы
 ,
, ,
, образуют трехмерный базис и представить
вектор
образуют трехмерный базис и представить
вектор в этом базисе.
в этом базисе.
|
а)
|
б)
|
в) другой ответ; |
г)
|
Вариант 14
Найти координаты вектора
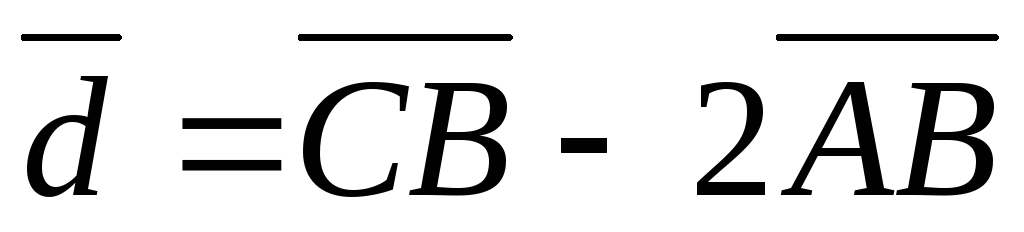 ,
если
,
если .
.а) (1;13);
б) (11; - 3);
в) (13; -5);
г) другой ответ.
Даны векторы
 ,
, .
При каком значении
.
При каком значении
 эти векторы перпендикулярны?
эти векторы перпендикулярны?а) 1;
б) –6;
в) 0;
г) другой ответ.
Найти вектор
 ,
коллинеарный вектору
,
коллинеарный вектору и удовлетворяющий условию
и удовлетворяющий условию .
.а)
 ;
;б) другой ответ;
в)
 ;
;г)
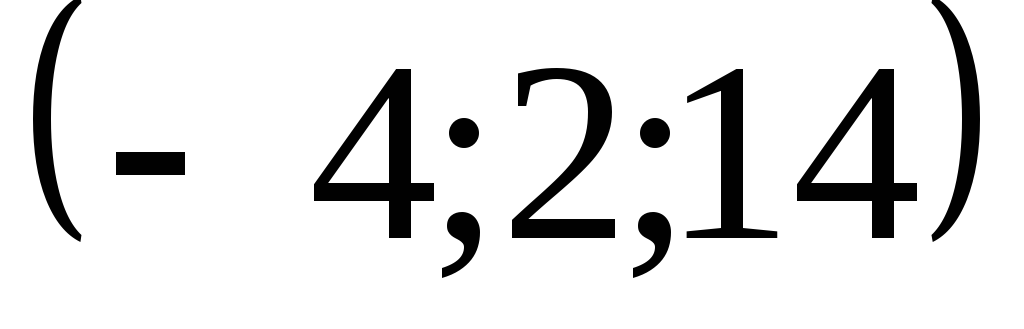 .
.Найти направляющие косинусы вектора
 .
.а)
 ;
;б)
 ;
;в)
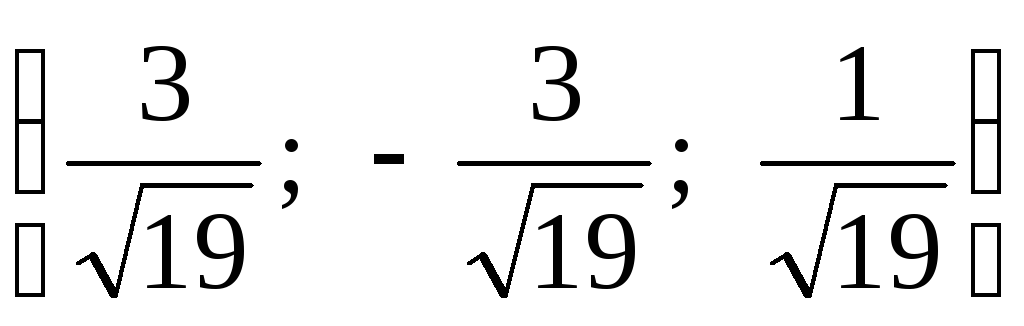 ;
;г) другой ответ.
Какой угол образуют единичные векторы
 и
и ,
если векторы
,
если векторы и
и взаимно перпендикулярны?
взаимно перпендикулярны?а)
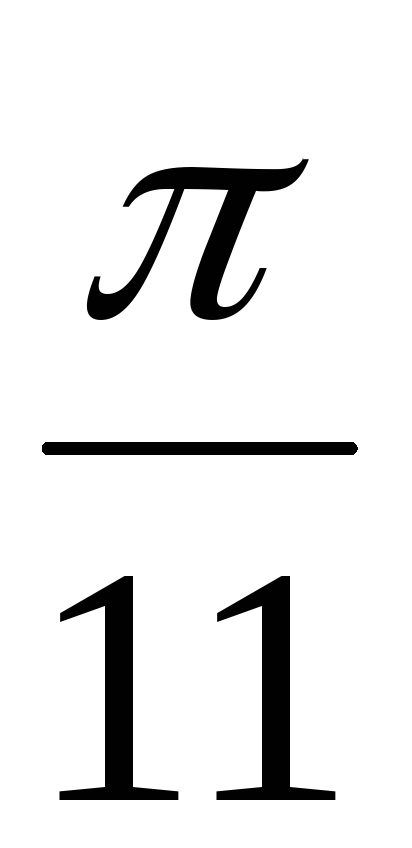 ;
;б)
 ;
;в) другой ответ;
г)
 .
.Даны две точки
 ,
, .
Точка
.
Точка делит отрезок
делит отрезок
 в отношении
в отношении .
Найти координаты точки
.
Найти координаты точки .
.а)
 ;
;б)
 ;
;в)
 ;
;г) другой ответ.
На плоскости даны точки
 ,
, ,
, .
В начале координат приложены силы
.
В начале координат приложены силы ,
, и
и .
Найти проекцию вектора
.
Найти проекцию вектора на равнодействующую сил
на равнодействующую сил .
.а)
 ;
;б) другой ответ;
в) 11;
г)
 .
.Показать, что векторы
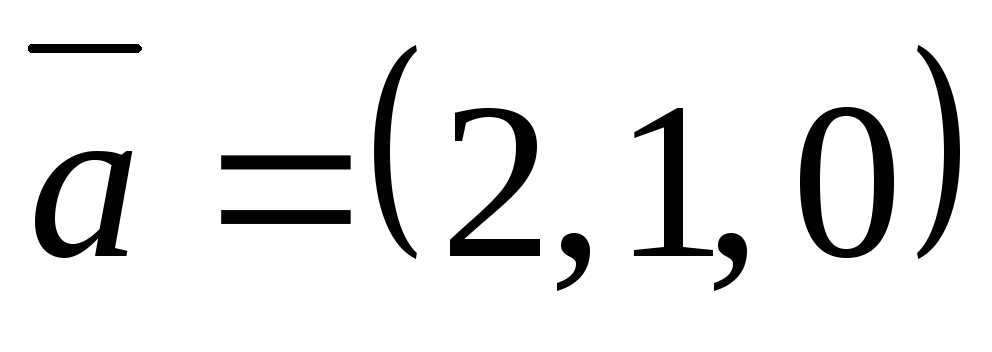 ,
, ,
, образуют трехмерный базис и представить
вектор
образуют трехмерный базис и представить
вектор в этом базисе.
в этом базисе.
|
а)
|
б)
|
в)
|
г) другой ответ. |
