1.2. Отображения и преобразования

Одним из фундаментальных понятий современной математики является понятие функции. Как известно, переменная y называется функцией переменной x, если каждому значению x, взятому из области её определения, отвечает одно или несколько значений y. Это записывают так: . Большое значение имеют однозначные функции, когда каждому значениюx соответствует единственное значение y (и наоборот).

Геометрическим аналогом понятия однозначной функции является отображение. Тогда под x и y понимают какие-либо геометрические образы: точки, прямые, плоскости, окружности…. Для конкретности в дальнейшем под x и y будем понимать точки.

Если даны два множества X(x₁, x₂, x₃…, x_i, x_n), Y(y₁, y₂, y₃…,y_i, y_n) и указано правило, по которому каждому элементу x_i множества X ставится в соответствие определённый элемент y_i множества Y, то говорят, что задано отображение f множества X в множество Y, и пишут: :(рис. 2). При этом элементy_i называется образом элемента x_i, а x_i – прообразом элемента y_i. Символическая запись читается: «в отображенииf элементу x соответствует элемент y» или «отображение f переводит x в y».

М

Рис. 2.

ножествоX называют областью определения (областью отправления), а Y - областью значений (областью прибытия) отображения f.

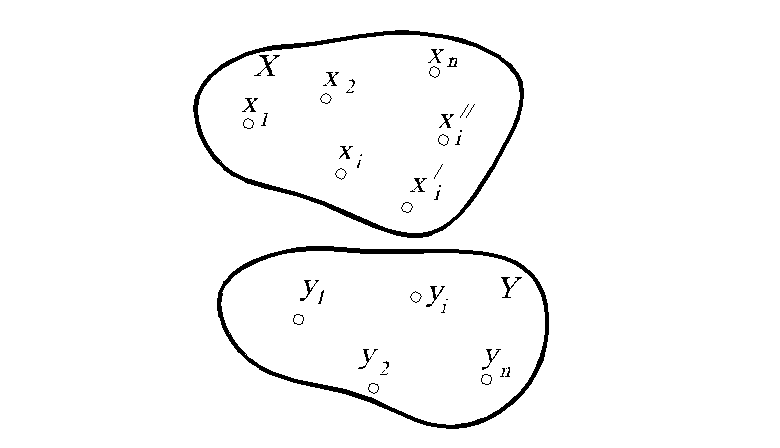
Пусть область определения X состоит из множества точек x₁, x₂, x₃…, x_i, x_n , а область значений Y – из множества точек y₁, y₂, y₃…,y_i, y_n (см. рис. 2). Следовательно, при отображении любой точке x_i в области X соответствует единственный образ y_i в области Y, но точка y_i может иметь несколько прообразов . Следовательно, обратное соответствиеявляется в этом случае неоднозначным.

Т

Рис. 3.

аким образом, об отображении можно говорить, если заданы два множества и некоторое правило или закон, по которому элементы множеств образуют пары, причем эти множества по этому закону, вообще говоря, не равноправны.

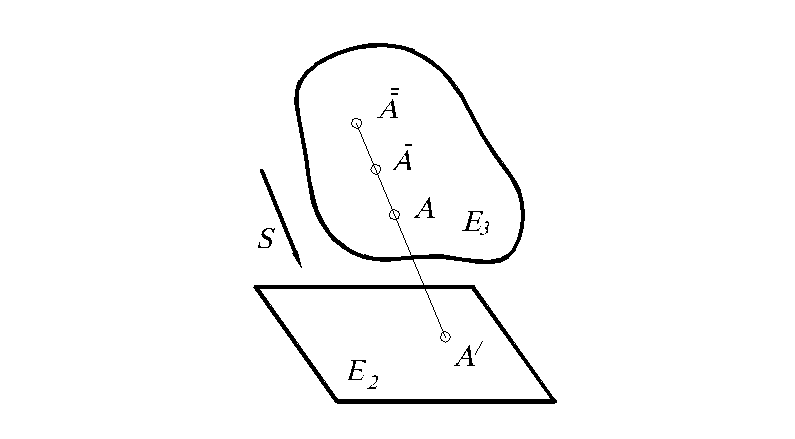
Наглядной иллюстрацией сказанного является отображение точек трёхмерного пространства на плоскость (двумерное пространство)путём параллельного проецирования (рис. 3): каждая точкаА трёхмерного пространства в данном направленииS проецируется в единственную точку плоскости. Однако в точкупроецируется не только точка, но и все точки.

Рассмотрим пример. Пусть З – множество зрителей в фойе театра перед спектаклем, а К – множество кресел. Как узнать, что зрителей и кресел поровну? Конечно, можно подсчитать, но мы получим избыточную информацию, нас не интересует их количество. Однако если во время спектакля все места заняты, причем никто из зрителей не стоит в проходах и на каждом месте сидит только один театрал, то это означает, что эти множества равны, в противном случае – наоборот.

Рассмотрим другой пример. Пусть в классе находится множество учеников и множество стульев. Предположим, что после звонка на урок каждый ученик занял свое место, то есть свой стул. В этом случае можно сказать, что задано отображение множества учеников на множество стульев. При этом если на каждом стуле сидит только один ученик, никто не стоит в проходах и все места заняты (например, имеем в классе 30 учеников и 30 стульев), то есть каждому ученику соответствует один единственный стул, и, наоборот, каждому стулу соответствует единственный ученик. Такое отображение называют взаимно однозначным (иногда говорят: «взаимно однозначное соответствие»).

Отображение называется взаимно однозначным, если каждому элементу y_iY соответствует единственный прообраз x_iX (и наоборот), то есть прямое соответствие и обратное соответствиеявляются однозначными. Такое отображение называетсябиективным, или биекцией.

Взаимно однозначное соответствие между элементами множеств (или между множествами) может быть установлено различными способами. На рис. 4 такое соответствие между точками двух отрезков (или между отрезками) АВ и CD установлено прямыми, проходящими через точку S. При этом точке ХАВ соответствует точка YCD, что символически записывается так: ХY. Между этими отрезками можно установить соответствие так: ХY, если , гдеCY, CD, AB, AX – длины отрезков.

В

Рис. 4.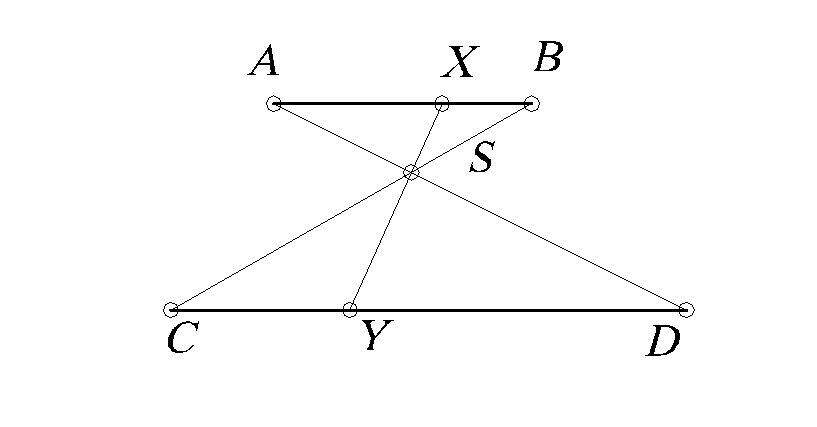

торое соответствие отличается от первого не только формой задания, но и парами соответствующих точек. Это можно заметить хотя бы по концам отрезка. В первом соответствииАD, BС, во втором – АС, BD. Этими двумя примерами не исчерпывается множество взаимно однозначных соответствий, которые могут быть установлены для точек данных отрезков.

Кроме этого, встречаются многозначные соответствия. Например, легковой машине соответствует 4 колеса, и наоборот. Такое отображение называется одно-четырёхзначное (14). Одно-двузначное отображение можно рассмотреть на примере действительных чисел, то есть каждому действительному числу соответствует пара рационального и иррационального чисел, и наоборот: 12.

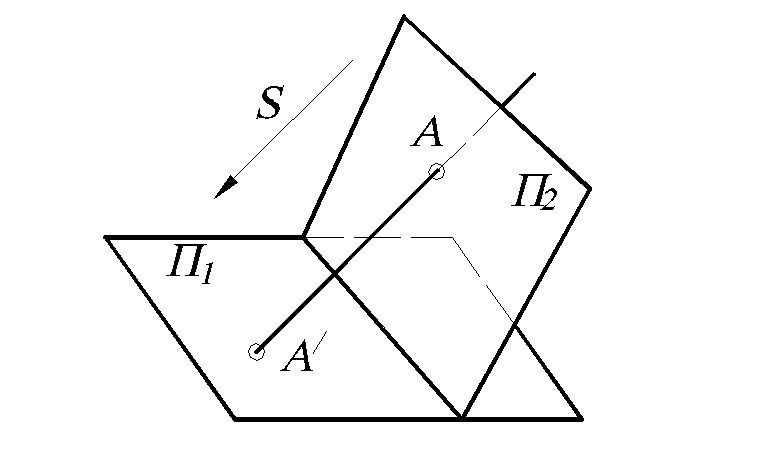
Примером обратимого соответствия является отображение двух плоскостей друг на друга при параллельном проецировании (рис. 5). Если в обратимом отображении область прибытия и область отправления – одно и то же множество М, то такое отображение называется отображением множества на себя, или преобразованием множества М.

О

Рис. 5.

тображение называетсяпреобразованием, если множества X и Y совмещены, то есть не только элементу x_i соответствует определённый элемент y_i, но и элементу y_i соответствует тот же элемент x_i. В этом случае говорят, что множество X отображается на себя X=Y. Другими словами, если отображение является обратимым, то оно называется преобразованием. Например, центральная симметрия точек пространства относительно некоторой точки О есть преобразование пространства.

Говоря о геометрическом преобразовании, обычно подразумевают, что М – множество точек плоскости или пространства. Если какое-то свойство фигуры F сохраняется в преобразовании f, то есть фигура обладает тем же свойством, то это свойство называетсяинвариантом преобразования.

Итак, преобразование – это взаимно однозначное отображение между всеми точками плоскости (или пространства), то есть правило, при котором каждой точке Р соответствует единственная точка Р^/, и, наоборот, каждой точке Р^/ соответствует единственная точка Р. Другими словами, правило, таким образом составляющее пары точек, что каждая точка Р плоскости (или пространства) ровно в одной паре стоит на первом месте и ровно в одной паре - на втором.

Может случиться, что обе точки пары окажутся одинаковыми. То есть что точка Р^/ совпадает с точкой Р. В этом случае точка Р называется неподвижной (двойной) точкой преобразования.

Результат последовательного выполнения нескольких преобразований называется их произведением, или композицией преобразований. Другими словами, преобразование, переводящее прообразы первого в образы второго при условии, что образы первого отождествлены с прообразами второго. Иначе говоря, если f(k) = m и g(m)=n, то произведение h=gf переводит k в n, то есть h(k)=n (преобразование, выполняемое первым, пишут справа!). Например, если f и g – повороты вокруг центра О на углы  и , то h=gf – поворот с той же осью на угол + (рис. 6, а). Если f – перенос на вектор АВ, а g – симметрия с центром О, то h=fg – симметрия с центром А, где 2АО=АВ (такое преобразование показано на рис. 6, б).

Здесь в первом примере произведение h=gf=fg, то есть не зависит от порядка сомножителей, то есть в этом случае говорят, что f и g перестановочны или коммутируют. Однако во втором примере произведение зависит от порядка сомножителей, то есть не коммутирует: fggf (сравните два рисунка – 6, а и 6, в или 6, а и 6, б).

А

а б в

Рис. 6.

налогично иногда результат двух операций зависит от порядка их выполнения, а иногда – и нет. Например, операции надевания левого и правого ботинковЛ и П перестановочны: ЛП=ПЛ, а операции надевания ботинка Б и носка Н – не коммутируют БННБ.