Глава 1 геометрические множества и системы координат

1. Множества

1.1. Основные понятия теории множеств

Понятие множества является одним из основных неопределяемых понятий математики. Вводя понятие «множество», обычно поясняют его смысл на примерах: библиотека – множество книг; алфавит – множество букв; лес – множество деревьев и т. д. В геометрии прямую, плоскость, пространство, прежде всего, понимают как множество точек.

Объекты, из которых состоит множество, называются его элементами. Множества имеют определённые характеристические свойства. Например, если имеем множество целых чисел, то буква не является элементом этого множества. Множество, элементы которого можно подсчитать, называется конечным множеством, в противном случае – бесконечным. Например, множество страниц книги конечно, так как его можно подсчитать; время – бесконечное множество. Если все элементы множества М являются частью множества N, то М называется подмножеством N. Например, прямая, лежащая в плоскости, является подмножеством множества точек плоскости. Другой пример: студенты одной группы являются подмножеством студентов всего института.

Рассмотрим основные теоретико-множественные понятия: 1) принадлежность (); 2) включение (); 3) пересечение (); 4) объединение (); 5) разность ( \ ); 6) пустое множество ():

1. Если m есть элемент множества М, записывают mM ; если m не принадлежит М, то пишут mМ. Множество, которое не содержит ни одного элемента, называется пустым множеством и обозначается . Точка является нульмерным множеством (это аксиома и определению не подлежит).

2. Если любой элемент множества М принадлежит множеству N, то М называют подмножеством множества N. Символическая запись: МN («множество М содержится в N»). При этом N называют надмножеством (объемлющим множеством) множества М.

3. Множество, состоящее из общих элементов нескольких множеств А, В, С, …, называется пересечением этих множеств и обозначается АВС,….

4. Объединение (или сумма) множеств М и N (М N) – это множество, элементами которого являются все элементы множества М и множества N.

5. Разностью множеств М и N называется множество, состоящее из элементов, принадлежащих М, но не принадлежащих N (M \ N). Если N М, то разность М \ N называют дополнением множества N в множестве М и обозначают 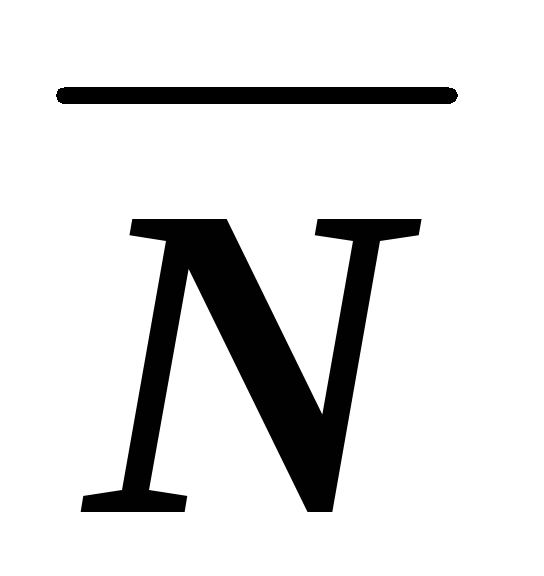; при этомN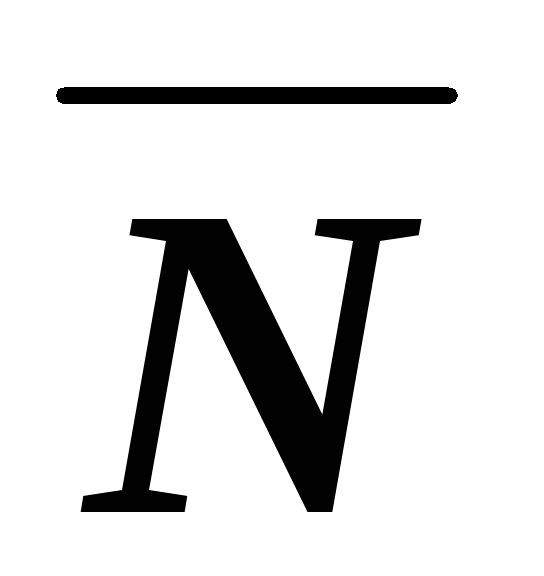=M.

Рассмотрим три множества точек, координаты которых удовлетворяют следующим уравнению и неравенствам (рис. 1):

Рис. 1.

Сфера: x² + y² + z² = 1 – C.

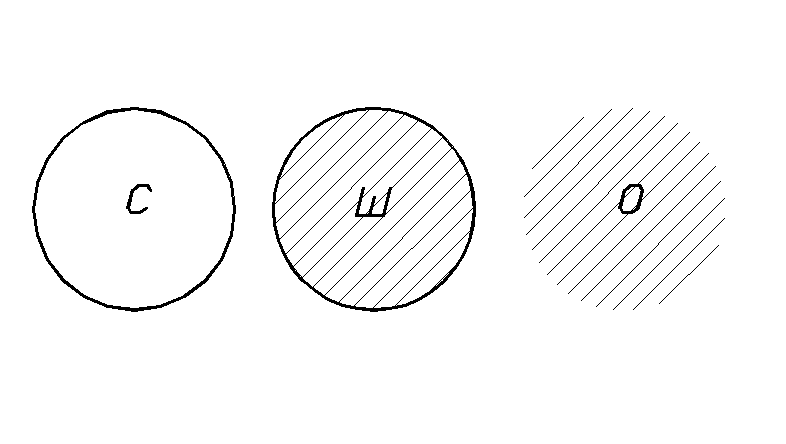
Шар: x² + y² + z² 1 – Ш.

Открытый шар: x² + y² + z² < 1 – О.

В этом случае справедливы следующие теоретико-множественные тождества:

СШ=С, ШО=О, СО=;

СШ=СО=ШО=Ш;

Ш\C=O, Ш\O=C, O\C=O, C\O=C;

С\Ш=О\Ш=; С=О, О=С, Ш=.

При определении пересечения трех и большего числа множеств пользуются следующими свойствами пересечения:

МN = NМ – коммутативность (то есть переместительный закон, выражающий независимость получаемого множества при пересечении множеств М и N от их перестановки);

(LM)N=L(MN) – ассоциативность (то есть сочетательный закон, выражающий независимость получаемого множества от замены некоторых множеств их пересечением);

ММ=М – идемпотентность (то есть результатом пересечения множества М самого с собой является множество М).

Операции пересечения, объединения, разности позволяют исходя из данных множеств строить новые множества. Другим же распространенным приемом конструирования множеств является то, что некоторые подмножества данного множества объявляются элементами нового множества. Рассмотрим несколько примеров.

ПРИМЕР 1. Множество прямых на плоскости называют плоским полем прямых. Элементами этого множества являются все прямые данной плоскости. Пучок прямых – множество прямых, проходящих по плоскости через данную точку (если эта точка несобственная (бесконечно удаленная), имеем пучок параллельных прямых).

ПРИМЕР 2. Множество прямых пространства называют линейчатым пространством. Примерами подмножеств линейчатого пространства могут служить следующие множества. Связка прямых – множество прямых пространства, проходящих через заданную точку (если эта точка несобственная, имеем связку параллельных прямых). Специальный линейчатый комплекс - семейство прямых, пересекающих данную прямую. Гиперболическая линейная конгруэнция – множество прямых, пересекающих две скрещивающиеся прямые (называемые ее осями или директрисами). Множество прямых, пересекающих три скрещивающиеся прямые, называется регулюсом, или линейчатой поверхностью.

ПРИМЕР 3. Пучок плоскостей – множество плоскостей, проходящих через заданную прямую (если прямая несобственная, имеют пучок параллельных плоскостей). Связка плоскостей – множество плоскостей, проходящих через заданную точку.

ОТНОШЕНИЕ ЭКВИВАЛЕНТНОСТИ

Пусть между элементами множества М определено некоторое отношение ~, то есть для любых двух элементов аМ и bМ известно а~b (читается «а эквивалентно b»). Это отношение должно удовлетворять следующим требованиям:

1) а~a - рефлексивность;

2) если а~b, то b~a - симметричность;

3) если a~b и b~c, то а~с - транзитивность.

Знак ~ называется отношением эквивалентности.

ПРИМЕР 1. В линейчатом пространстве параллельность прямых а, b, c,… является отношением эквивалентности, так как 1) а||а, 2) если а||b, то b||a, 3) если а||b и b||с, то а||с.

ПРИМЕР 2. Отношение перпендикулярности на множестве прямых плоскости симметрично (аb и ba), но не рефлексивно и не транзитивно и поэтому отношением эквивалентности не является.

В связи с заданием на множестве М отношения эквивалентности оно разбивается на непересекающиеся подмножества, называемые классами эквивалентности: в один класс входят эквивалентные между собой элементы. Пересечение любых двух классов пусто, а объединение всех классов эквивалентности есть М (М – это «слоеный пирог», а классы – это слои). Множество, элементами которого являются классы эквивалентности (слои), называется фактор-множеством множества М по отношению к эквивалентности ~. Фактор-множество в примере 1 – это множество связок параллельных прямых.

Два множества называются эквивалентными, если между их элементами можно установить взаимно однозначное соответствие. Под взаимно однозначным соответствием будем понимать такое соответствие, при котором любому элементу одного множества ставится в соответствие единственный элемент другого множества, и, наоборот, любым различным (не совпадающим) элементам одного множества соответствуют различные элементы другого множества, задействованы все элементы обоих множеств.

Об эквивалентных множествах говорят, что они имеют одинаковую мощность. Эквивалентные конечные множества состоят из одного и того же числа элементов. Если бы это было не так, то при установлении взаимно однозначного соответствия каким-то элементам не было бы соответствующих. В случае конечных множеств понятие мощности совпадает с понятием числа элементов.