8.2. Средняя квадратичная погрешность результата измерения с весом единица

При оценке неравноточных измерений в качестве единицы меры точности используют среднюю квадратичную погрешность, соответствующую измерению с весом равным единице. Ради краткости ее называют квадратичной погрешностью единицы веса.

По определению веса

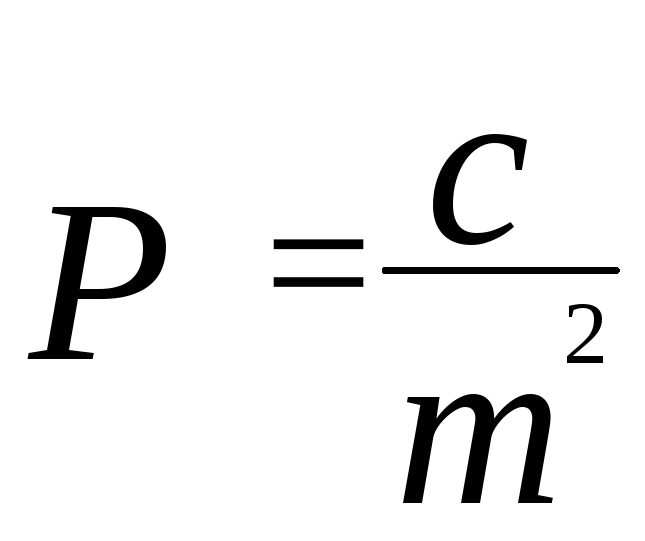, подставим ² вместо m²: ,

отсюда: следовательно, меняется с изменением коэффициента «С». Поскольку «С» может быть любой величиной, то подставим вместо нее ², тогда:

и тогда: ;;,

т.е. средняя квадратичная погрешность любого результата измерения равна погрешности измерения с весом равным единице, деленной на корень квадратный из веса этого результата.

Пример: Средняя квадратичная погрешность измерения

m = 4. Вес измерения Р_m = 1. Тогда, средняя квадратичная погрешность измерения с весом равным единице:

, .

Средняя квадратичная погрешность измерения с весом 3 равна

, .

Допустим, имеется ряд неравноточных измерений (l_i) каждое из которых содержит случайную погрешность (_i) и вес (p_i):

l₁‚ l₂‚ … l_n

₁, ₂, … _n

p₁, p₂, … p _n

Для каждого измерения можно записать:

µ² = m₁²P₁

µ² = m₂²P₂

. . . . . .

µ² = m_n ²P_n

Сложим левые и правые части равенств и разделив их на n, получим:

, ,

При достаточно большом количестве измерений можно записать:

m²P = ²P т. к.

, отсюда m² = ² и

:

средняя квадратичная погрешность с весом равным единице равна корню квадратному из дроби, в числителе которой сумма произведений квадратов абсолютных погрешностей неравноточных измерений на их веса, а в знаменателе – количество неравноточных измерений.

8.3. Средняя квадратичная погрешность общей арифметической середины

Поскольку для любого результата измерения

, то погрешность М₀общей арифметической середины

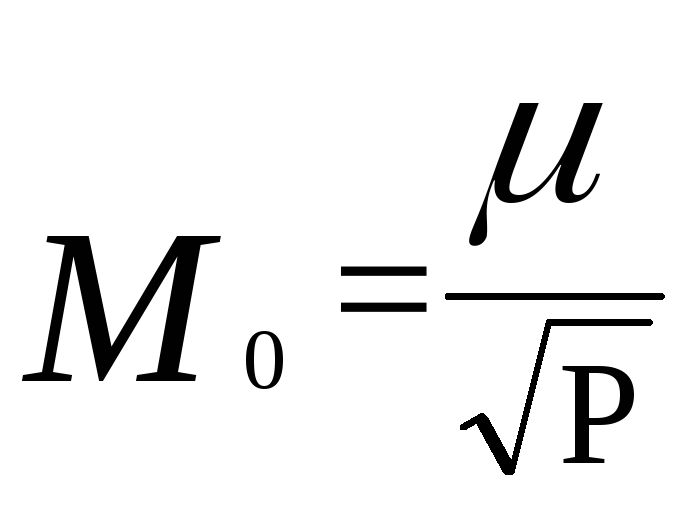, где Р = р, поэтому

подставим значение 

.

Вывод:средняя квадратичная погрешность общей арифметической середины равна корню квадратному из дроби, в числителе которой сумма произведений квадратов абсолютных погрешностей неравноточных измерений на их веса, а знаменатель – произведение количества измерений на сумму их весов.

Вероятнейшие погрешности неравноточных измерений и их свойства.

Вероятнейшая погрешность есть отклонение результата измерения от арифметической середины:

V₁ = I₁ – L₀

V₂ = I₂ – L₀

. . . . .

V_n = I_n – L₀

Умножив левую и правую части на соответствующие веса, получим:

V₁P₁ = I₁ P₁ – L₀ P₁

V₂ P₂= I₂ P₂ – L₀ P₂

. . . . .

V_n P_n = I_n P_n – L₀ P_n

VP=lP–L₀P

т. к. lP=L₀P, тоVP= 0, следовательно:

сумма произведений вероятнейших погрешностей неравноточных измерений на их веса равна нулю

Если для равноточных измерений принять все веса равными единице, то

V= 0.

т. е. сумма вероятнейших погрешностей равноточных измерений равна нулю.

Эти формулы используют для контроля вычисления L₀ иV_i

Формула Бесселя для вычисления средней квадратичной погрешности неравноточных измерений с весом равным единице

, надежность оценки .

Формула для вычисления средней квадратичной погрешности вероятнейшего значения

.

Таблица 1 - Пример вычислений

li	p	v	vp	v2	v2 p
3400	1	-45	-45	2025	2025
3455	2	10	20	100	200
3454	3	9	27	81	243
L0=3445	p = 6		vp=2		 v2p =2468

, , ,

, , , X = 344514.