Вопросы для самоконтроля

1) Какие вопросы рассматривает теория погрешностей геодезических измерений?

2) Основные задачи теории погрешностей?

3) Какие предварительные расчеты имеет возможность выполнять инженер-

землеустроитель на основе знания теории погрешностей геодезических измерений?

4) Что является математической основой теории случайных погрешностей?

5) Какое событие называют случайным?

6) Как вычислить частость (Р*) события?

7) Чему равна сумма частостей всех событий какого-либо ряда измерений

физической величины?

8) Случайной величиной в теории погрешностей называют?

9) Какую характеристику связи дает Закон распределения случайных величин

между их значениями?

10) В чем заключается различие между случайными независимыми и зависимыми друг

от друга величинами?

11) Математическим ожиданием случайной величины Х называют?

12) Какие свойства имеет математическое ожидание?

СПИСОК ЛИТЕРАТУРЫ

Основная

1. Маслов А.В., Гордеев А.В., Батраков Ю.Г. Геодезия. М.: «КолосС», 2006.- 298 с.

2. Неумывакин Ю.К., Смирнов А.С. Практикум по геодезии. М. «КолосС», 2007.

Дополнительная

1. Лысов А. В., Шиганов А.С. Геодезия. Методические указания по изучению дисципл

ны и выполнению курсовой работы студентами 2 курса очной и 3 курса заочной формы обучения специальностей 120301 “Землеустройство” и 120302. ФГОУ ВПО «Сарат. Гос. Агр. Ун-т им. Н.И. Вавилова», Саратов, 2007.- 52 с.

Лекция 7 Случайные погрешности геодезических измерений

7.1. Дисперсия, среднее квадратичное отклонение

Дисперсией D(X) случайной величины X называется число, определяемое как

,

это есть математическое ожидание квадрата разности случайной величины и ее математического ожидания

Среднее квадратичное отклонение _x случайной величины X называют положительное значение квадратного корня из дисперсии этой величины

Величина  характеризует средний разброс (дисперсию) значений X_i вокруг

истинного значения Х случайной величины. Она является общепринятой теоретической оценкой погрешности измерений, т. е. степени приближения значения величины полученного в результате измерений, к истинному значению этой величины.

7.2. Средняя квадратичная погрешность

На практике сложность заключается в том, что измерения выполняются не бесконечное число, а какое-то ограниченное число раз. Поэтому для оценки точности измерений используют приближенную оценку среднего квадратичного отклонения, которую называют средней квадратичной погрешностью.

Допустим, что выполнено n измерений одной и той же линии. Получен ряд значений х₁, х₂, . . .х_n измеряемой величины с абсолютными погрешностями по каждому измерению: ₁, ₂, . . . _n.

Из результатов измерений исключены грубые и систематические погрешности. Тогда ₁, ₂, . . . _n представляют собой лишь случайные абсолютные погрешности измерений. Если далее значения полученных погрешностей показать на горизонтальной числовой оси влево со знаком минус и вправо со знаком плюс, а на вертикальной оси – соответственно количество таких погрешностей (рис.1.), то получится график зависимости между количеством случайных погрешностей и их величиной, который выражает закон Гаусса (закон нормального распределения). Из этого закона вытекают свойства случайных погрешностей равноточных измерений физической величины:

1. Большие погрешности измерений повторяются реже (маловероятны).

2. Абсолютные величины погрешностей не превышают определенного предела.

3. Абсолютные величины погрешностей не превышают определенного предела.

4. Среднее арифметическое из значений случайных погрешностей данного ряда измерений стремится к нулю при неограниченном возрастании количества измерений.

Сложив почленно левую и правую части полученных равенств получим, что истинное значение Х = Хn /n измеряемой величины отличается от среднеарифметического ее значения Х₀ = Х_i /n на бесконечно малую величину

(₁, + ₂ , + . . . + _n.) / n = _ср (бесконечно малая величина), если количество измерений достаточно велико: Х₀ – Х = _ср.

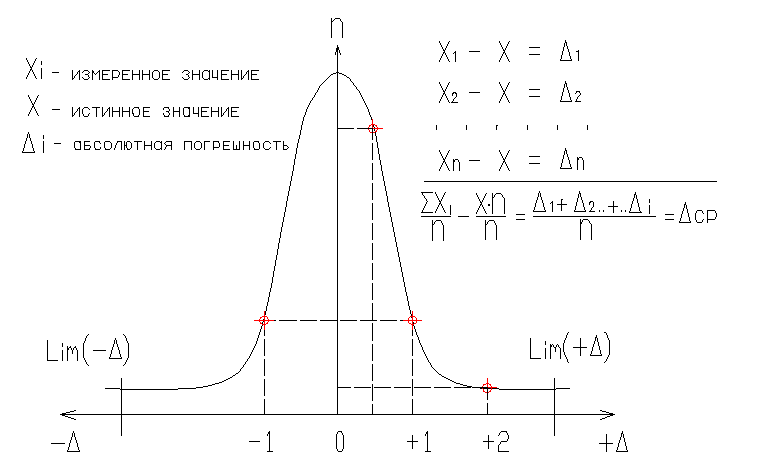
Рисунок 1. График зависимости случайных погрешностей от их величин

Отсюда истинное значение Х измеряемой величины равно:

Х = Х₀ – _ср.

Это очень важное обстоятельство используется в теории ошибок геодезических измерений. Поскольку истинное значение Х измеряемой величины определить совершенно точно не представляется возможным, то его можно заменить средним арифметическим значением Х₀ и назвать вероятнейшим значением измеряемой величины, (или арифметической серединой).

В практике геодезических вычислений за истинное значение измеряемой величины может быть принято значение, полученное более совершенным (более точным) техническим средством. Например, при оценке точности измерений мерной лентой, за истинное значение измеряемой линииможет принят результат ее измерения точным светодальномером. Или, например, выполняется измерение угла на плане транспортиром. За истинное значение этого угла может быть принят результат его измерения на местности точным геодезическим прибором и т. д.

Как определить среднюю случайную погрешность измерения, если имеется ряд измерений физической величины? Первое, что приходит на ум найти среднее арифметическое из суммы случайных погрешностей этого ряда измерений. Разберем числовой пример, (таб.1.). Здесь представлены результаты шестикратного измерения линии местности. Среднее значение X₀=484.18 м. Каждое измерение имеет погрешность по абсолютному значению не превышающую 0.10 м. Если же вычислить среднюю погрешность данного ряда измерений, то она равна нулю, поскольку алгебраическая сумма погрешностей равна нулю, т.е. это идеальное измерение.

Таблица 1 - Вычисление средней погрешности

n	х		2
1	484.23	+0.05	0.0025
2	484.20	+0.02	0.0004
3	484.16	-0.02	0.0004
4	484.27	+0.09	0.0081
5	484.08	-0.10	0.0100
6	484.14	-0.04	0.0016
N=6	X0=484.18	=0	2=0.0230

х – измеренное значение величины

X₀ - среднее значение измеряемой величины

 - погрешность измеряемой величины

Этого не может быть никогда. При таком подходе можно ошибаться в ту или другую сторону на огромные величины, а средняя погрешность все равно нуль. Такой подход к оценке средней погрешности не годится.

Тогда, может быть, можно оценить среднюю погрешность измерений по абсолютным значениям случайных погрешностей, (т. е. без учета из знака, таб. 2.):

Таблица 2. Вычисление средних погрешностей

n		
1	6	6
2	4	2
3	8	14
4	4	4
5	2	2
6	0	2
7	8	10
8	6	0
9	4	6
10	6	2
n = 10	=4.8	=4.8

В таб. 7.2. приведены два ряда по 10 измерений одной физической величины. В каждом ряду измерений сумма погрешностей одинакова и равна 10. Однако, второй ряд измерений выполнен грубее, с большими погрешностями. Поэтому и такой способ подсчета средней погрешности не годится.