3. Управление запасами

3.1. Вводные замечания и основная модель

Как правило, предприятия создают различного рода запасы: сырье, комплектующие изделия, незавершенное производство, готовую продукцию, предназначенную для реализации. Совокупность подобных материалов, представляющих временно не используемые экономические ресурсы, называются запасами предприятия.

Запасы создаются по разным причинам. Одной из них является необходимость обеспечения непрерывности производственного процесса. Дефицит сырья или комплектующих изделий может привести к сбоям в работе предприятия и к остановке производства. Поэтому на складах всегда поддерживается необходимый уровень запасов. Запасов не должно быть ни слишком много, ни слишком мало. В первом случае возникает необходимость неоправданных затрат на хранение и амортизацию товара, во втором может возникнуть дефицит и, как следствие, сбои в процессе производства. Малое количество запасов подразумевает их частое пополнение, а перевозки мелкими партиями приводят к увеличению затрат на транспортировку. Из этих соображений следует, что в каждом отдельном случае должна существовать некоторая оптимальная величина запаса, при которой достигается минимальное значение издержек по поддержанию этого запаса.

Задача управления запасами и состоит в том, чтобы избежать обеих крайностей и, по возможности, уменьшить общие затраты.

Основная модель

Важнейшую роль в наших рассуждениях будет играть функция из­менения запаса (рис. 3.1). Это связь между количеством единиц товара на складе (обозначим его через Q) и временем t. Считаем, что имеется один вид товара и спрос на товар равномерен во времени. Тогда на графике изменения запаса этот процесс будет изображаться прямой линией с отрицательным коэффициентом наклона. Мы будем считать возможным мгновенное по­полнение запаса. Такой процесс на графике будет изображаться вертикальной прямой.

Если на товар имеется спрос, то функция изменения запаса f(t) убывает. Если товар, наоборот, завозят на склад, то эта функция возрастает (рис. 3.1). Пусть в начальный момент времени запас имеет максимальное значение, равное q. При равномерном спросе он будет полностью израсходован через некоторое время τ.

Затраты, связанные с запасами, можно разделить на три части.

а). Стоимость товара C₁.

б). Организационные издержки C₂. Это расходы, связанные с офор­млением товара, его доставкой, разгрузкой, учетными операциями, зарплатой работникам склада, занятым обработкой заказа и т. д.

Q

t q f(t) τ

Рис. 3.1

в). Издержки на хранение товара C₃. Это затраты на аренду склада, стоимость содержания складских помещений (охрана, освещение, отопление), страховые платежи, амортизацию в процессе хранения и т. д.

Рассмотрим основные величины и предположения относительно

них, принятые в рамках основной модели. Мы будем в основном ис­пользовать в качестве единицы измерения денежных средств услов­ные единицы (УЕ), это могут быть рубли, доллары и т. п.; в качестве единицы измерения времени — год.

1. Цена единицы товара — с УЕ. Цена постоянна, при этом рассматрива­ется один вид товара.

2. Интенсивность спроса или годовая потребность — d единиц товара в год. Будем считать, что спрос постоянный и непрерывный.

3. Организационные издержки — s УЕ за одну партию товара. Бу­дем считать, что организационные издержки не зависят от размера поставки, т. е. от количества единиц товара в одной партии.

4. Издержки на хранение запаса — h УЕ на единицу товара в год. Будем считать эти издержки постоянными.

5. Размер одной партии товара постоянен — q единиц. Партия поступает мгновенно в тот момент, когда возникает дефицит, т. е. когда запас на складе становится равным нулю.

Все эти предположения соответствуют процессу на рис.3.1. Он состоит из повторя­ющихся циклов пополнения запаса между двумя соседними дефи­цитами. Параметры с, d, s, h считаются заданными. Задача управления запасами состоит в выборе параметра q таким образом, чтобы мини­мизировать годовые затраты.

Для решения сформулированной задачи надо прежде всего выра­зить эти затраты через параметры с, d, s, h, q.

1. Поскольку годовая интенсивность спроса равна d, а цена еди­ницы товара — с, то общая стоимость товара в год равна

cd.

2. Поскольку в одной партии q единиц товара, а годовой спрос равен d, то число поставок равно d/q. В течение года организацион­ные издержки равны

(d/q) · s.

3. Средний уровень запаса равен отношению площади под гра­фиком за цикл к продолжительности цикла. Этот средний уровень равен q / 2 (на рис. 3.1 обозначен пунктиром). Поскольку годовые из­держки на хранение единицы товара равны h, то общие издержки на хранение составляют

(q / 2) · h.

Рис. 3.2

Таким образом, общие издержки С вычисляются по формуле

C = C₁+C₂+C₃ = cd + + . (3.1)

Напомним еще раз, что в рамках модели параметры с, d, s, h счи­таются заданными и требуется найти такое число q*, чтобы функция С = C(q) принимала наименьшее значение на множестве q > 0 имен­но в точке q*.

График функции С = C(q) показан на рис. 3.2. Его нетрудно получить, рассмотрев выражение (3.1). В самом деле, второй член этого выражения представляет собой гиперболу, т. е. с ростом q будет убывать. Третий член с ростом q будет линейно расти. Суммируя оба эти графика по точкам нетрудно получить зависимость, как на рис.3.2. Первый член выражения от q не зависит, а лишь переместит результирующий график несколько выше.

Для нахождения точки q* минимума функции С = C(q) найдем ее производную (с, d, s, h — фиксированные числа):

C′(q) = (cd)′ + ( )′ + ( )′ = − + .

Приравнивая C'(q) к нулю, получаем:

− + = 0.

Отсюда можно найти q*:

q*= . (3.2)

Полученная формула называется формулой оптимального размера заказа или экономически обоснованного размера заказа (Economic Order Quantity, EOQ). Часто эту формулу называют формулой Уилсона или Вильсона (Wilson). В некоторых источниках формулу называют формулой Харриса (Harris).

Примечание. Надо отметить, что модель управления запасами, приводящая к «формуле квадратного корня» для оптимального размера заказа, предложена Ф. Харрисом в 1913 г., но получила известность после публикации широко известной работы Р. Уилсона в 1934 г., а потому часто называется моделью Вильсона. Формула Харриса была выведена для оптимальной партии изделий, запускаемых в производство (optimal batch) и выглядит следующим образом:

,

где x₀ — размер оптимальной партии; D — общая (годовая) потребность в деталях данного вида; s — расходы на подготовку оборудования к новой партии; q — расходы на хранение одной детали.

Несоответствие заказываемого размера партии оптимальному значению приводит к увеличению издержек на содержание запаса и организацию поставок. Покажем, что это так. При q = q* из (3.1) имеем:

C – C₁ = C – cd = + = .

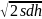Предположим, что вместо оптимального размера партии была заказана партия, равная 2 q*, тогда из уравнения издержек (3.1) следует:

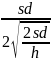C′ – C₁′ = + = = (C – C₁).

Таким образом, заказ партии товара 2 q* (вместо q*) приведет к увеличению общих издержек на содержание запасов и организацию поставки на 25 %. Аналогичная картина наблюдается в случае заказа партии товара меньшей, чем q*.

Пример 3.1. Пусть интенсивность равномерного спроса состав­ляет 1200 единиц товара в год. Организационные издержки равны 8 УЕ, издержки на хранение — 3 УЕ на единицу товара в год, цена товара — 5,5 УЕ.

Определить оптимальный размер партии предполагая, что система подчиняется основной модели.

Решение. Условие, переписанное в терминах формулы Уилсона имеет вид:

d = 1200, s = 8, h = 3, с = 5,5.

Подставляя в формулу, получаем:

q* = = = .

Замечание. Найдя оптимальный размер заказа, можно определить оптимальное число поставок за год n* и соответствующую продол­жительность цикла изменения запаса t*:

n* = d / q = 1200 / 80 = 15,

t* = 365 / n* = 365 / 15 24 дня.