9. Динамические модели

9.1. Модель народонаселения

Интересно, что построить математическую модель часто совсем не­трудно. Нередко для этого используются самые простые и легко объ­яснимые предположения.

Предположим, что речь идет о численности населения какого-либо населенного пункта. Знание о том, с какой скоростью растет население, весьма важно для построения планов, например, строительства общественных зданий. Во времена, когда эта модель была создана – конец XVIII, начало XIX веков - общественными зданиями в основном были церкви, и вопрос о том, стоит или не стоит строить новую церковь, и каких размеров, был часто весьма актуален. Так что по ходу наших рассуждений можно говорить о количестве жителей или прихожан.

Обозначим через х_n количество жителей к концу n−го года. Их численность через год, т. е. к концу (n + 1)−го года, естественно обо­значить через х_n+1. Тогда изменение численности за этот год можно описать разностью

Δх_n = х_n+1 − х_n.

Оно происходит по двум естественным причинам — люди рождают­ся и умирают (для простоты будем считать, что миграции и других причин изменения численности населения нет). Определить число родившихся и число умерших за год по приходским книгам, например, особого труда не соста­вляет. Просмотрев записи и подсчитав число родившихся и умерших в разные годы, можно сопоставить полученные числа

b₁,…,b_k

и

d₁,…,d_k

с общим числом жителей за эти годы

х_1,...,х_к

и отметить, что отношения

b₁/ х₁,…,b_k /х_к,

год от года различаются весьма мало. То же касается и отношений

d₁/ х₁,…,d_k / х_к.

Для простоты расчетов будем считать эти отношения постоянны­ми и обозначим их через α и β соответственно.

Тем самым число родившихся в n-м году оказывается равным

b_n = α х_n,

а число умерших –

d_n = β х_n.

Изменение численности населения по естественным причинам составит

Δх_n = + α х_n − β х_n.

Население в n + 1 году выразится через численность населения в n –м году как:

х_n+1 = х_n + Δх_n = х_n + α х_n − β х_n = х_n(1+ α – β).

Положим

γ = 1+ α – β.

Тогда интересующая нас формула примет вид

х_n+1 = γ х_n . (9.1)

Можно считать модель построенной. Эта модель называется математической моделью роста народонаселения Мальтуса в итерационной форме.

Попробуем теперь разобраться с тем, что же получилось, т. е. про­анализировать построенную модель.

Возможны три случая:

1) γ > 1 (δ = α — β > 0 — рождается больше, чем умирает) и численность прихожан растет год от года,

2) γ = 1 (δ = α — β = 0 — умирает столько же, сколько рождается) и численность прихожан год от года остается неизменной,

3) γ < 1 (δ = α — β < 0 — умирает больше, чем рождается) и численность прихожан неуклонно снижается.

Так как побудительным мотивом для построения модели было желание узнать, как быстро будет расти число прихожан, начнем с рассмотрения первого случая.

Случай 1. γ > 1. Итак, численность прихожан растет. Но как, насколько быстро?

xn n xn x0 n

Рис. 9.1

Обратим внимание на то, что числовая последовательность роста населения представляет собой геометрическую прогрессию со знаменателем γ. Если обозначить через х₀ численность населения в начальный период, в год с индексом 0, мы получаем следующую геометрическую прогрессию:

х_n = х₀ γⁿ. (9.2)

При любом γ > 1 картинка, иллюстрирующая изменение х_n, име­ет похожий вид − х_n будет расти экспоненциально. Вид этой зависимости представлен на рис.9.1. Чтобы почувствовать, как быстро происходит рост в соответствии с этой зависимостью, положим γ = 1,02. Это означает 2 % прироста населения каждый год. Так вот, через 36 лет γ³⁶ будет равна с точностью до шестого знака после запятой 2,039887, то есть население удвоится относительно первоначальной численности. Нетрудно подсчитать, что 36×56 = 2016, и что γ²⁰¹⁶ = (γ³⁶)⁵⁶ ≈ 2⁵⁶ > 10¹⁴. Численность населения Земли не дотягивает до этой цифры. О чем это говорит? Лишь о том, что модель имеет свои границы применимости. Она неплохо описывает рост народонаселения на промежутках в несколько лет, но как видим, дает неверный результат на больших временных промежутках.

В 1820 г. в Лондоне Т. Р. Мальтусом была опубликована работа "Principles of political economy considered with a view to their practical application" (в русском переводе - "Опыт о законе народонаселения ..." Т. 1-2. СПб., 1868), в которой, в частности, говорилось о том, что в силу биологических особенностей людей население имеет тенденцию размножаться по закону геометрической прогрессии:

х_n+1 = γ х_n , γ 1,

в то время как средства существования могут увеличиваться лишь по закону арифметической прогрессии:

y_n+1 = y_n + d, d 0.

Такое различие в скорости изменения величин, непосредственно связанных с проблемами выживаемости популяции, не мо­гло остаться незамеченным и вызвало довольно жесткую критику и сильно политизированную полемику в общественных кругах, которая продолжалась довольно долго.

Важный вывод. Предлагая построенную или выбранную вами модель, вы непременно должны указать пределы, в которых ею мож­но пользоваться, и предупредить о том, что нарушение этих ограни­чений может привести (и, скорее всего, приведет) к серьезным ошиб­кам. Коротко говоря, у каждой модели есть свой ресурс.

Случай 2. γ = 1. Численность населения не изменяется (рис. 9.2).

Случай 3. γ < 1. Население вымирает (рис. 9.3).

n xn	n xn
Рис. 9.2	Рис. 9.3

Мы умышленно весьма подробно остановились на описании моде­ли народонаселения, во-первых, потому, что она является одной из первых моделей подобного рода, и, во-вторых, чтобы на ее приме­ре показать, через какие основные этапы проходит решение задачи построения математической модели.

Очень часто, описывая эту модель народонаселения, привлекают ее дифференциальный вариант:

= δх.

Здесь подразумевается, что х = x(t) — зависящая от времени численность популяции, — производная по времени, δ — некоторая постоянная величина. Решением этого уравнения является функция:

x(t) = x₀ , (9.3)

где x₀ – численность населения в момент времени t = 0 (9.3) называют математической моделью народонаселения Мальтуса в дифференциальной форме. Положив в (9.3) γ = e^δ, можно убедиться, что мы переходим к формуле (9.2). Нетрудно установить связь между коэффициентом γ = 1 + α – β из (9.1) и коэффициентом δ из (9.3). Для этого запишем равенство:

γ = e^δ ,

следовательно

δ = = 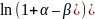. (9.4)

При больших значениях x конкурентная борьба за средства существования приводит к уменьшению δ, и эта жесткая модель должна быть заменена более мягкой:

= δ(х) х,

в которой коэффициент δ зависит от численности населения. В про­стейшем случае эта зависимость описывается так:

δ(х) = а — bх,

где а и b — постоянные числа, а соответствующее уравнение прини­мает вид

= ах — bх². (9.5)

Это уравнение можно записать в виде, более удобном для анализа:

, (9.6)

где . Это уравнение называется логистическим уравнением и известно также как уравнение Ферхюльста.

x

0 t

Рис.9.4

Таким образом, мы приходим к более сложной, так называемой логистической модели, которая описывает динамику популяции уже достаточно хо­рошо. Анализ логистической кривой (рис. 9.4) весьма поучителен, и его проведение может быть любопытно читателю.

Точным решением уравнения (9.6) является выражение:

,

где К можно трактовать как ёмкость среды, т. е. максимально возможную численность населения, а – начальная численность населения. Исходя из сказанного, можно записать:

К сказанному следует добавить, что логистическая модель хорошо описывает и другие процессы, на­пример эффективность рекламы, жизненный цикл товарного образца.

В наших рассуждениях, которые привели к модели роста народонаселения Мальтуса в итерационной форме, можно было бы говорить не только росте населения людей, но и о росте популяции любых живых организмов. Суть рассуждений можно было бы для этого не менять. Положим, что речь идет о популяции рыб. Положим также, что к модели (9.1) добавляется некая квота отлова рыбы за время каждого такта, описываемого моделью. Получается экспоненциальная модель роста популяции в итерационной форме с отловом:

х_n+1 = γ х_n – с. (9.7)

Рис. 9.5

На рис. 9.5 изображены расчеты нескольких траекторий х_n по формуле

х_n+1 = 1,1х_n – 0,05

при изменении n от 0 до 30. Положив в (9.7) х_n+1 = х_n, можно получить значение стационарной траектории:

х_стац. = . (9.8)

Траектория с х₀ = 0,5 является для выбранной зависимости стационарной и критической. Падение популяции ниже этого уровня ведет, как видно из рис. 9.5 к монотонному уменьшению популяции с той или иной скоростью и ее гибели. Можно привести и экономическую интерпретацию модели роста популяции с отловом. Под х_n можно подразумевать прибыль организации за n-ый период времени, γ может означать способность организации зарабатывать эту прибыль, а с может обозначать постоянные выплаты, которые не зависят от прибыли. Модель иллюстрирует существование некоторого критического размера изначальной прибыли, при превышении которой возможен дальнейший ее неограниченный рост. И напротив, если уровень этой прибыли ниже критического, то в будущем прибыль будет только сокращаться.

В заключение этого раздела следует упомянуть еще об одной современной модели народонаселения, предложенной С. П. Капицей в 1992 году в статье «Математическая модель роста народонаселения мира». Эта модель базируется на том факте, обнаруженном автором, что рост населения Земли происходит пропорционально квадрату полной численности людей. Этот факт принципиально выделяет человека из животного мира, для которого характерно, что скорость роста каждого вида пропорциональна числу особей (при отсутствии ограничений). Уравнение роста народонаселения мира можно в этом случае записать как:

dN/dt = aN². (9.9)

Обосновать такую закономерность можно следующим образом. Рост населения мира (N), например, с 10 до 100 млн. человек подразумевает, что и уровень развития жизнеобеспечивающих технологий вырос приблизительно в 10 раз. С другой стороны, десятикратный рост численности населения означает и десятикратный рост числа потенциальных ученых и изобретателей, а значит, и десятикратное возрастание относительных темпов технологического роста. Вывод следующий: с ростом численности населения в 10 раз абсолютная скорость технологического роста вырастет в 10 × 10 = 100 раз (в соответствии с уравнением (9.9)).

Решением дифференциального уравнения (9.9) является гиперболическое уравнение вида

N_t = 1/a(t₀ — t). (9.10)

С. П. Капицей предложено следующее представление этой формулы с введенными в нее эмпирическими коэффициентами:

N = C/(T₁ − T) = 186/(2025 − T) млрд, (9.11)

где N − число людей на Земле в момент времени T, T₁ − критическая дата в нашем летоисчислении, С − постоянная с размерностью [человекогоды].

Эта формула, хотя и имеет ограниченную область применения (неточна как в далеком прошлом, так и в ближайшем будущем), но все же дает приемлемые оценки искомой величины в последние 1,6 млн лет развития человечества.

Автор определил предел стабилизации народонаселения мира в 75 миллиардов и дал оценку общего числа людей, когда-либо живших, в 100 миллиардов.

Важно отметить, что, рассматривая информационную природу численности народонаселения Земли, он приходит к утверждению о «единстве развития Человечества как целого» и необходимости «рассматривать его как некую мировую структуру, глобальный суперорганизм, охваченный общим информационным взаимодействием. Это утверждение возникает как существенный вывод из всей рассматриваемой концепции».