
- •Экономико-математические методы и модели в социально-экономических исследованиях
- •Экономико-математические методы и модели в социально-экономических исследованиях
- •Информационные ресурсы дисциплины
- •Модель границы производственных возможностей
- •Возможности и потребности. Модели и реальность
- •1.2. Альтернативная стоимость. Издержки и выбор
- •1.3. Экономический рост и эффективность
- •Графы, сети и их применение в экономике
- •Основные определения и характеристики графов. Плоские графы
- •2.2. Ориентированные графы. Построение минимального остовного дерева сети
- •2.3. Задача нахождения кратчайшего пути. Дерево решений
- •2.4. Сетевые графики
- •3. Управление запасами
- •3.1. Вводные замечания и основная модель
- •3.2. Модель производственных поставок. Модель поставок со скидкой
- •3.3. Модель управления запасами, включающая штрафы
- •3.4. Обобщенная модель определения оптимального размера партии
- •4. Распределение ресурсов
- •4.1. Постановка задачи распределения ресурсов. Механизм прямых приоритетов
- •4.2. Механизм обратных приоритетов. Конкурсный механизм
- •4.3. Механизм открытого управления
- •4.4. Открытое управление и экспертный опрос
- •5. Математические модели в финансовых операциях
- •5.1. Простые проценты. Сложные проценты
- •5.2 Начисление процентов в условиях инфляции.
- •5.3. Погашение кредита. Балансовое равенство
- •5.4. Балансовое уравнение
- •Иерархии и приоритеты
- •6.1. Приоритеты. Измерения и согласованность. Идеальные измерения
- •6.2. Обратно-симметричные и согласованные матрицы. Индекс согласованности
- •6.3. Вычисление собственных характеристик обратно-симметричной матрицы
- •6.4. Проблема сравнения. Построение шкал. Иерархии
- •7. Методы прогнозирования
- •7.1. Анализ временных рядов. Метод подвижного (скользящего) среднего.
- •7.2. Метод проецирования тренда
- •7.3. Прогнозирование с учетом сезонной вариации. Аддитивная модель
- •7.4. Мультипликативная модель. Каузальные методы прогнозирования. Качественные методы прогнозирования
- •8. Основы управления рисками в экономике
- •8.1. Риски в экономике. Оптимизация портфелей банка
- •8.2. Диверсификация портфеля
- •8.3. Достижимое и эффективное множества
- •8.4. Выбор оптимального портфеля
- •9. Динамические модели
- •9.1. Модель народонаселения
- •9.2. Модель мобилизации
- •9.3. Модель гонки вооружений
- •9.4. Модель хищник – жертва
- •Глоссарий
- •Библиографический список
- •Порядковые номера дней в невисокосном году
- •Порядковые номера дней в високосном году
- •Предметный указатель
- •Оглавление
2.2. Ориентированные графы. Построение минимального остовного дерева сети
Ребро графа G(X, Т) называется ориентированным, или дугой, если одну вершину считают началом, а другую концом этого ребра.
На рисунке дугу обозначают стрелкой. Дугу с началом в вершине xi и концом в вершине xj записывают (xi, xj).
Определение2.7. Граф, все ребра которого ориентированы, называется ориентированным графом.
Число дуг, исходящих из вершины ориентированного графа xi, называется полустепенью исхода вершины xi, число дуг, входящих в вершину xi, − полустепенью захода вершины xi.
Вершина xi называется источником, если ее полустепень захода равна нулю, и стоком, если ее полустепень исхода равна нулю.
Рассмотрим ориентированный граф на рисунке 2.26. Полустепень исхода вершины х1 равна 1, полустепень захода этой вершины – 2, степень вершины х1 равна 3. Вершина х3 является источником, вершина х2 – стоком.
|
|
Рис. 2.25 |
Рис. 2.26 |
Определение 2.8. Последовательность дуг (x1, x2), (x2, x3), …, (xk-1, xk), в которой конец предыдущей дуги совпадает с началом следующей, называется маршрутом от x1 до xk .
Маршрут, в котором первая и последняя вершины совпадают, называется замкнутым.
Пример 2.6. Рассмотрим ориентированный граф (Рис. 2.26). Он имеет множество маршрутов, например: (х1, х2), (х2, х6), (х6, х7), (х7, х3), (x3, х2), (х2, x6), (х6, х5), (х5, х1). Этот маршрут является замкнутым.
Маршрут, в котором все вершины различны, называется путем от x1 до xk.
Если существует путь из вершины xi в вершину xj, то говорят, что xj достижима из xi.
Замкнутый путь называется контуром.
Рассмотрим ориентированный граф (Рис. 2.27). Он имеет пути (х4, х1), (х1, х2), (х2, х3) и (x1, х2); (х2, х4), (х4, х3), а также один контур (х4, x1), (х1, х2), (х2, х4). Вершина хз достижима из вершины х1.
Полным ориентированным графом называется граф G(X, Т), в котором каждая пара вершин соединена в точности одной дугой.
Ориентированный граф, изображенный на рис.2.28, является полным.
|
|
Рис. 2.27 |
Рис. 2.28 |
Ориентированный граф G(X,T) можно задать с помощью матрицы инцидентности. Пусть x1, x2, ..., хn — вершины графа, 11, 12, …, lm — дуги графа.
Определение 2.9. Матрицей инцидентности ориентированного графа G(X, T) называется матрица Вn х m, у которой элемент bij равен 1, если дуга lj исходит из вершины xi, равен (−1), если дуга lj входит в вершину xi; равен 0, если дуга lj и вершина xi не инцидентны.
Пример 2.7. Для ориентированного графа, изображенного на рис. 2.29, матрица инцидентности имеет следующий вид:
1 0 0 -1 0 -1 1 0 0 1 0 -1 -1 0 0 0 0 1 1 -1
4 |
x1 l1 x2
|
Рис. 2.29 |
|
Построение минимального остовного дерева сети. В экономических приложениях графы принято называть сетями, а их вершины — узлами. Каждому ребру (дуге) придают некоторое числовое значение, которое в зависимости от смысла задачи может обозначать расстояние, пропускную способность, время и т. д. С каждым видом сети связан определенный тип потоков, например, поток нефти в нефтепроводах, автомобильные потоки в сети городских дорог).
Определение 2.10. Остовным деревом сети называется дерево, содержащее все узлы сети.
Пример 2.8. Рассмотрим сеть с пятью узлами (рис. 2.30, а). Для этой сети можно построить множество остовных деревьев. Некоторые примеры таких остовных деревьев изображены на рис. 2.30, б-е.

x1 x2 x3 x4 x5 

|
x1 x2 x3 x4 x5 |
а |
б |
x1 x2 x3 x4 x5 |
x1 x2 x3 x4 x5 |
в |
г |
x1 x2 x3 x4 x5 |
x1 x2 x3 x4 x5 |
д |
е |
Рис. 2.30 |
|
При изучении сетей возникает задача построения минимального остовного дерева, т. е. задача соединения всех узлов сети с помощью путей наименьшей длины. Примером такой задачи является проектирование сети дорог между населенными пунктами, где дороги, соединяющие два пункта, могут проходить через другие населенные пункты. Наиболее экономичный проект должен минимизировать общую длину дорог.
Рассмотрим процедуру построения минимального остовного дерева. Введем обозначения:
X = { х1, х2 , …, хn} — множество узлов сети;
Ck — связное множество узлов сети, соединенных алгоритмом после выполнения k− ой итерации;
 — множество
узлов сети, не соединенное с узлами
множества Ck
после
выполнения
k−
ой итерации;
— множество
узлов сети, не соединенное с узлами
множества Ck
после
выполнения
k−
ой итерации;
Минимальное остовное дерево строят по следующему алгоритму:
выбирают произвольный узел сети хi: С1 = хi ,
 =
X
\ {х};
=
X
\ {х};выбирают из оставшихся узлов узел Xj, ближайший к множеству узлов С1: С2 = Xi,.xj,
 = X
\ {xi,
Xj};
= X
\ {xi,
Xj};выбирают из множества узел, ближайший к узлам множества С2, включают его в множество С2 и исключают из множества .
За
конечное число шагов будут обработаны
все узлы сети и построено минимальное
остовное дерево: Сn
=
X,
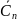 =
=
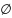 .
.
Пример 2.9. Телевизионная компания планирует подключение к кабельной сети пяти новых районов. Структура планируемой сети и расстояния между пунктами (в км.) заданы на рис. 2.31, а. Требуется спланировать кабельную сеть наименьшей длины.
Проведем
пошаговое построение минимального
остовного дерева для данной
сети. Со =
,
 = {
х1,
х2,
х3,
х4,
х5,
х6}.
Начнем
с узла x1.
= {
х1,
х2,
х3,
х4,
х5,
х6}.
Начнем
с узла x1.
Итерация 1 (рис. 2.31, б):
С1 = {х1}. = {х2, х3, х4, х5, х6}, min(1,5,7,9) = 1.
Ближайший узел к множеству С1 — узел х2. Добавляем его к остовному дереву с ребром длиной 1 км.
Итерация 2 (рис. 2.31, в):
С2 = {х1 , х2}. = {х3, х4, х5, х6}. min(3,4,5,6,7,9) = 3.
Ближайший узел к множеству С2 — узел х5. Добавляем его к остовному дереву с ребром длиной 3 км.
Итерация 3 (рис. 2.31, г):
С3
= {х1,
х2,
х5}.
 = {х3,
х4,
х6}.
min(4,5,6,7,8)
= 4.
= {х3,
х4,
х6}.
min(4,5,6,7,8)
= 4.
Ближайший узел к множеству Сз — узел х4. Добавляем его к остовному дереву с ребром длиной 4 км.
Итерация 4 (рис. 2.31, д):
С4
= {x1,
х2,
х4,
х5},
 = {х3,
х6},
min(3,5,6)
= 3.
= {х3,
х6},
min(3,5,6)
= 3.
Ближайший узел к множеству С4 — узел х6. Добавляем его к остовному дереву с ребром длиной 3 км.
Итерация 5 (рис. 2.31, е):
С5
= {x1,
х2,
х4,
х5,
х6},
 = {х3},
min(5,6,10)
= 5.
= {х3},
min(5,6,10)
= 5.
Ближайший узел к множеству С5 — узел х3. Добавляем его к остовному дереву с ребром длиной 5 км. При этом возможно два альтернативных соединения (х1, х3) и (х4, х3) длиной 5 км. Процесс построения минимального остовного дерева завершен (рис. 2.31, ж).
Итак,
С6
= X
=
{
x1,
х2,
х3,
х4,
х5,
х6},
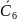 =
.
Минимальная
длина телевизионного кабеля составит
1 + 3 + 4 + 3 + 5 = 16 км.
=
.
Минимальная
длина телевизионного кабеля составит
1 + 3 + 4 + 3 + 5 = 16 км.
|
|
а |
б 3 3 |
3 3
6 5 |
3 6 8
|
в 3 3 |
г |
|
|
д |
е |
|
|
|
ж |
|
Рис. 2.31 |

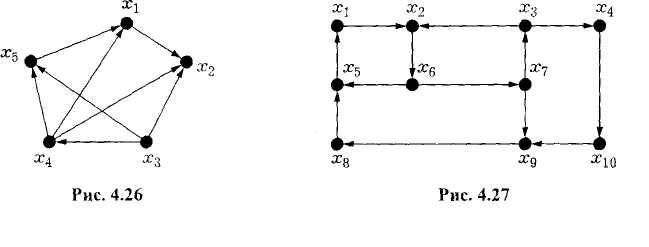








 5
5











