9.4. Модель хищник – жертва

В модели Мальтуса рассказывалось о беспрепятственном размножении популя­ции. Однако в реальных обстоятельствах популяция сосуществует с другими популяциями, находясь с ними в самых разных взаимо­отношениях.

Здесь мы коротко рассмотрим антагонистическую пару хищник - жертва (это может быть и пара рысь – заяц, лиса – кролик, и пара божья коровка − тля) и попытаемся проследить, как может изменяться со временем численность обеих взаимодействующих сторон.

Предполагаем, что популяция жертвы может существовать сама по себе, поскольку питается растительной пищей, в то время как популяция хищника существует только за счет жертвы.

Обозначим численность популяции жертвы через х, а численность популяции хищника – через у.

В отсутствие хищника жертва размножается согласно уже известному уравнению

= αх, α > 0,

а хищник в отсутствие жертвы вымирает по закону

= β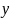 , β > 0.

Хищник съедает количество жертвы, пропорциональное ее собственной численности и численности хищника. Поэтому при наличии хищника численность жертвы меняется по закону

= α х γ xy, γ > 0.

Съеденное количество жертвы способствует размножению хищника, что можно записать так:

= − βу + δ ху, δ > 0.

Таким образом, мы получаем систему уравнений, которая носит имя модели Вольтерра-Лотки:

= αx γxy,

= βy + δxy, (9.24)

причем

0, 0,

Модель хищник – жертва построена.

Как и в предыдущей модели, наибольший интерес для нас представляет точка равновесия (х*, у*), где = 0 и = 0, а х* и у* представляют собой отличное от нуля решение системы уравнений:

αx γxy = 0

βy + δxy = 0,

или

x (α γ y) = 0, y( β + δ x) = 0. (9.25)

Координаты точки равновесия M*, являющейся точкой пересечения прямых

αx γxy = 0, (9.26)

βy + δxy = 0 (9.27)

легко вычисляются (рис. 9.14):

х*= β/δ, у*= α/γ.

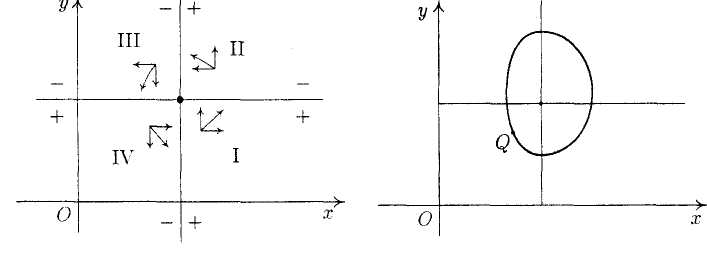
Начало координат О (0,0) лежит в положительной полуплоскости относительно горизонтальной прямой, задаваемой уравнением (9.26), а относительно вертикальной прямой, задаваемой уравнением (9.27), − в отрицательной полуплоскости (рис. 9.15).

Первую четверть – а нас по-прежнему интересует только она, так как х 0 и у 0 – можно разбить, действуя аналогично только что изложенному, на четыре области, которые удобно обозначить так:

I – (+,+), II – (−,+), III – (−,−), IV – (+,−).

x y O M* α/γ β/δ	x y O III II I IV
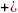
Рис.9.14	Рис.9.15

Пусть начальное состояние Q (х₀,у₀) находится в области IV. Тогда выполнены неравенства

α γ y₀ 0, β + δ x₀ 0,

из которых следует, что скорости и в этой точке должны иметь разные знаки

> 0, < 0,

и, значит, величина х должна возрастать, а величина y убывать.

Подобным же образом анализируя поведение х и у в областях I, II и III, получим в итоге картину, изображенную на рис. 9.16.

Рис. 9.16 Рис. 9.17

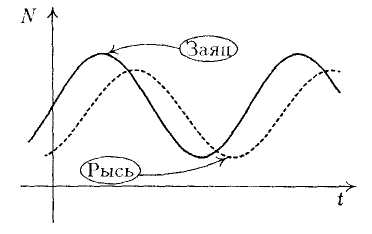
Отклонение от состояния равновесия приводит к колебаниям численности жертвы и хищника вокруг точки равновесия (рис. 9.18). Так, если в некоторый момент времени система находится в точке Q, то с течением времени она опять вернется в эту точку, если на систему не будет оказано дополнительного воздействия.

Аналогичными уравнениями описывается поведение гармонического осциллятора. По аналогии с гармоническим осциллятором, поведение системы хищник – жертва не является структурно устойчивым. Небольшое изменение модели, например, учет ограниченности ресурсов, необходимых жертве, может привести к качественному изменению поведения системы. Может случиться, что равновесное состояние станет устойчивым, и колебания численности будут затухать. Возможен и противоположный сценарий, когда любое малое отклонение от положения равновесия приведет к катастрофическим последствиям, вплоть до полного вымирания одного из видов. Однако на вопрос о том, какой из этих сценариев реализуется, модель Вольтерра — Лотки ответа не дает: здесь требуются дополнительные исследования.

Как показывают наблюдения, несмотря на свою простоту, пред­ложенная модель качественно верно отражает колебательный ха­рактер численности в системе хищник − жертва (рис. 9.18). Увеличение популяции зайца должно привести к увеличению популяции рыси с некоторым сдвигом по времени. Вмешиваться в действия непонятных нам законов природы иногда довольно опасно, поскольку можно нарушить отлаженное столетиями равновесие в природе. Так, например, непродуманное применение инсектици­дов (если только они не уничтожают насекомых практически пол­ностью) в конечном счете приводит к увеличению популяции тех насекомых, численность которых находится под контролем других насекомых-хищников. Примером может послужить следующий факт.

	Божья коровка
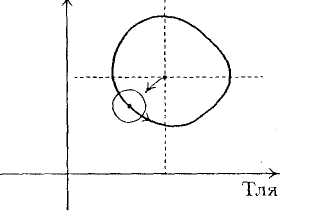
Рис. 9.18	Рис. 9.19

Случайно попавшая в Америку тля поставила под угрозу все про­изводство цитрусовых. Вскоре туда же был завезен ее естественный враг — божья коровка, которая немедленно принялась за дело и сильно сократила популяцию тли. Чтобы ускорить процесс уничто­жения, фермеры применили ДДТ, но в результате количество тли увеличилось. Воздействуя в первую очередь на божью коровку, препарат привел к сокращению ее популяции и соответственно к росту популяции тли, что, глядя на рис. 9.19, нетрудно предугадать.

В заключение главы следует сказать, что построение модели, как правило, опирается на значительное упрощение изучае­мой ситуации, и, следовательно, к получаемым на ее основе выво­дам нужно относиться достаточно осторожно. Модель может описать отнюдь не все тонкости того или иного процесса. Вместе с тем даже весьма грубая на вид идеализация нередко позволяет глубже вникнуть в суть проблемы. Пробуя как-то влиять на параметры модели (выбирая параметры, меняя их), мы получаем возможность подвергнуть исследуемое явление качественному ана­лизу и сделать выводы общего характера.

Следует упомянуть одну из современных экономических моделей – магистральную теорию, или магистраль. В математической экономике магистралью называется траектория экономического роста, на которой пропорции производственных показателей (такие как темп роста производства, темп снижения цен) неизменны, а сами показатели (такие как интенсивность производства, валовый выпуск) растут с постоянным максимально возможным темпом. Таким образом, магистраль - это траектория или луч максимального сбалансированного роста. Ее часто сравнивают со скоростной автострадой. Это образное сравнение принадлежит Дорфману, Самуэльсону и Солоу. Допустим, что некто хочет проехать по большому городу из пункта А в пункт Б. Если пункты А и Б расположены недалеко друг от друга, то скорее всего самый быстрый путь − это самый короткий. Однако если расстояние между А и Б велико, то самый быстрый путь оказывается чаще всего таким: надо из А выехать на одну из больших городских магистралей, где средняя скорость движения достаточно высока, не смущаясь тем, что мы, возможно, движемся в сторону от цели Б, по этой магистрали приблизиться, насколько возможно, к пункту Б и затем только с нее свернуть. Именно так возник научный термин "магистраль".

Поскольку "оптимальное" или "эффективное" развитие экономики в любом смысле так или иначе связано и должно сопровождаться экономическим ростом, то для достижения любой конечной цели следует поступать аналогичным образом: сначала вывести производство на магистральный путь, т. е. на так называемую траекторию (или луч) Неймана, характеризующуюся максимальным темпом роста и минимальной нормой процента 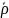= , а по истечении определенного срока времени вывести ее к задуманной цели. Такими целями могут быть максимизация прибыли, минимизация затрат, максимизация полезности от потребления товаров, достижение конкурентного равновесия при наиболее благоприятных условиях, т. е. на более высоком уровне благосостояния населения, и т. д.

Итак, с одной стороны мы имеем магистральные модели, а с другой − оптимизационные или еще шире − нормативные модели экономики. Изучение этих двух моделей во взаимосвязи, т. е. изучение связи между магистральными и оптимальными (в том или ином смысле) траекториями и является предметом магистральной теории. Можно говорить, что магистральная теория является одним из средств качественного анализа оптимальных траекторий.

Вопросы для самопроверки

1. Пользуясь моделью Мальтуса определить количество лет, за которое население удвоится, если γ равно 1,01; 1,02; 1,03; 1,04; 1,05.

Ответ: ≈ 70; ≈35; ≈23; ≈18; ≈14.

2. Определить стационарную траекторию в модели роста популяции с отловом, если коэффициент роста γ =1,05, а квота отлова составляет 0,05.

Ответ: 1.

3. Определить, какова будет численность населения через 50 лет в соответствии с логистической моделью роста, если коэффициент а = 0,003, исходная численность населения составляет 150 млн, а ёмкость среды равна 50 млрд.

Ответ: 174266676.

4. Определить численность населения Земли в 1700 году, пользуясь моделью Капицы.

Ответ: 0,57 млрд.

Заключение

Предлагаемый учебный курс по экономико-математическим моделям и методам призван дать студентам первоначальную подготовку в области построения математических моделей и их применения на практике. Успешное освоение предлагаемых глав позволит, по замыслу составителя, перейти к изучению специализированных учебных курсов, предусмотренных программой обучения, таких как «Экономико-математические методы и модели в логистике», «Логистика снабжения», «Управление запасами в цепях поставок» и т. д.