3.2. Модель производственных поставок. Модель поставок со скидкой

В основной модели предполагалось, что поступление товаров на склад происходит мгновенно. Это предположение достаточно хоро­шо отражает ситуацию, когда товар поставляется в течение одного дня (или ночи). Если товары поставляются с работающей производ­ственной линии, необходимо модифицировать основную модель. В этом случае к параметрам с, d, s и h добавляется еще один — интенсивность поставки товара с производственной линии р (единиц товара в год). Будем считать ее заданной и постоянной.

Эта модель называется моделью производственных поста­вок. Величина q по-прежнему обозначает размер поставляемой партии. В начале каждого цикла происходит "подключение" к производственной ли­нии, которое продолжается до накопления М единиц товара. После этого пополнения запасов не происходит до тех пор, пока не возник дефицит. График функции изменения запаса имеет вид, изображенный на рис. 3.3.

q

τ р = q M t τ M/2

Рис.3.3

Общие издержки C(q), как и в основной модели, состоят из трех частей.

A. Общая стоимость товара в год равна

cd.

Б. Годовые организационные издержки равны

.

В. Издержки на хранение вычисляются следующим образом. Пусть τ − время поставки (рис. 3.3). В течение этого времени проис­ходит как пополнение (с интенсивностью p), так и расходование (с интенсивностью d) запаса. Увеличение запаса происходит со скоростью p − d. Поэтому достигнутый к концу периода пополнения запаса максимальный его уровень М вычисляется по формуле

M = (p – d) τ . (3.3)

Если расходование товара отсутствует, то за время τ при интенсивности производства p будет произведено q единиц товара, т. е. p · τ = q (см. рис. 3.3). Из последнего равенства следует, что

τ = . (3.4)

Следует отметить, что M < q, что очевидно из сравнения (3.3) и (3.4). Из (3.3) и (3.4) следует, что

M = (p – d) .

Средний уровень запаса по аналогии с основной моделью равен полови­не максимального, т. е. М/2. Таким образом, издержки на хранение запаса равны

Общие издержки вычисляются по формуле

C= cd + + . (3.5)

Оптимальный размер поставки получаем, приравнивая первую производную нулю:

C′= − + = 0.

Отсюда:

q* = . (3.6)

Пример 3.2. Интенсивность равномерного спроса составляет 1200 единиц товара в год. Товар поставляется с конвейера, произ­водительность которого составляет 5200 единиц в год. Организаци­онные издержки равны 8 УЕ, издержки на хранение — 3 УE, цена единицы товара — 5,5 УЕ. Чему равен оптимальный размер партии?

Решение. Условие задачи в терминах формулы выглядит следующим образом:

d = 1200, p = 5200, s = 8, h = 3, c = 5,5.

Подставляя значения в выведенную формулу:

q* = = .

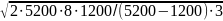Замечание. Найдя оптимальный размер заказа, можно определить оптимальное число поставок за год n* и соответствующие продолжительность поставки τ* и продолжительность цикла пополнения запаса t*:

n* = d/ q* = 1200 / 91 ,

τ* = q*/ p = (91 / 5200) 365 дней,

t* = 365 / n* = 365 / 9 28 дней.

Модель поставок со скидкой. Рассмотрим ситуацию, описываемую в целом основной моделью, но с одной особенностью, которая состоит в том, что товар можно поста­влять по льготной цене (со скидкой), если размер партии достаточно велик. Иными словами, если размер закупаемой партии q не менее заданного чи­сла q₀, товар поставляется по цене c₀, где с₀ < с.

Функция общих издержек C(q) задается в таком случае следую­щим образом:

		cd + sd/q + qh / 2, если q < q0
C(q) =			(3.7)
		c0d + sd/q + qh / 2, если q q0

Очевидно, что функция в точке q₀ имеет разрыв.

Обе функции

f(q) = cd + sd/q + qh / 2

и

f₀(q₀) = c₀d + sd/q + qh / 2

имеют минимум в точке, где

f ′(q) = f ′₀(q₀) = 0

т. е. в точке, определяющей оптимальный размер партии поставки, т. е.

q* = .

Возможны три следующие варианта (см. рис. 3.4):

а). q₀ < q*, т. е. величина закупаемой партии, при которой реализуется скидка, окажется меньше величины оптимальной партии, определяемой формулой Уилсона. Минимум издержек будет в точке минимума функции издержек (на нижней ветви функции т.к. функция терпит разрыв в точке q₀) в точке q*. Решением будет закупка партии величиной q′=q*.

б). q₀ = q*, т. е. величина закупаемой партии, при которой реализуется скидка, окажется равной величине оптимальной партии, определяемой формулой Уилсона. Очевидно, и в этом случае решением задачи будет закупка партии величиной q′=q*.

в). q₀ > q*, т. е. величина закупаемой партии, при которой реализуется скидка, окажется больше величины оптимальной партии, определяемой формулой Уилсона. Для выяснения вопроса о том, какой размер партии оптимален, следует вычислить и сравнить значения функции C(q) в точках q₀ и q*, и та точка, где функция C(q) принимает меньшее значение, будет оптимальным размером партии q′ в модели поставок со скидкой.

С q q С С С q0 = q* q* q0 q* q0 q′ = q0 q q q0 q*	С q
а	б	в
Рис. 3.4

Пример 3.3. Предположим, что интенсивность равномерного спроса составляет 1200 единиц товара в год. Организационные из­держки равны 8 УЕ, издержки на хранение — 3 УЕ. Цена единицы товара равна 5 УЕ, однако, если размер партии не менее 500 единиц, цена снижается до 4 УЕ. Найти оптимальный размер партии.

Решение. Условие задачи можно переписать в виде:

d = 1200, s = 8, h = 3, с = 5, q₀= 500, с₀ = 4.

Общие издержки определяются функцией C(q):

		f(q)=6000+9600/q+3q/2, если q < 500
C(q) =
		f0(q)=4800+9600/q+3q/2, если q 500

= = =

Поскольку q₀ > q*, то следуя варианту в):

C(q) = f(q) = f(80) =6000+9600/80+3 80/2=6240.

В точке q = q₀ получаем

C(q₀) = f₀(q₀) = f₀(500) 4800+9600/500+3·500/2=5569,2.

Решением задачи является величина партии q′ = 500.