7.2. Метод проецирования тренда

Основной идеей метода проецирования (линейного) тренда (trend projection) является построение прямой, которая "в среднем" наименее уклоняется от массива точек (t_i, x_i), i = 1, 2,..., n, заданного временным рядом (рис. 7.10).

Эта прямая ищется в следующем виде:

x = at + b, (7.4)

где a и b – постоянные, подлежащие определению.

t x t1 t2 t3 ti tn a ti + b x = a t + b

Рис. 7.10

Чтобы найти коэффициенты a и b, поступают так: для каждого значения t_i переменной t, пользуясь формулой (7.4), вычисляют соответствующее значение переменной х:

at_i + b, i = 1, 2,..., n,

находят разность

at_i + b − x_i, i = 1, 2,..., n,

которую затем возводят в квадрат (чтобы не думать о знаке):

( at_i + b − x_i)², i = 1, 2,..., n,

и, складывая, в итоге получают некоторую вспомогательную функцию, которую мы обозначим φ(a,b):

φ(a,b) = →min. (7.5)

Требуется отыскать минимум этой функции. Функция φ(a,b) принимает минимальное значение в том случае, когда величины a и b удовлетворяют следующей линейной системе:

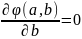
Находя частные производные, приходим к системе уравнений:

= 0

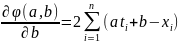= 0. (7.6)

Систему (7.6), сгруппировав иначе переменные под знаками суммы и, перенеся суммы, содержащие , в правую часть уравнений, можно переписать в виде:

a + bn = ,

a + b = . (7.7)

Эта система всегда имеет единственное решение. Уравнения (7.7) называются также нормальными уравнениями.

Решая систему уравнений (7.7), например методом Гаусса, приходим к выражениям для а и b:

;
.	(7.8)

Можно указать простой и общий способ составления нормальных уравнений. Используя опытные точки и уравнение (7.4), можно записать систему уравнений для a и b:

x₁= at₁ + b

x₂= at₂ + b

………….

x_n= at_n + b

Умножим левую и правую части каждого из этих уравнений на коэффициент при первой неизвестной a (т. е. на t₁, t₂, ..., t_n) и сложим полученные уравнения, в результате получится второе нормальное уравнение из (7.7). Умножим левую и правую части каждого из этих уравнений на коэффициент при второй неизвестной b, т. е. на 1, и сложим полученные уравнения, в результате получится первое нормальное уравнение из (7.7). Этот способ получения нормальных уравнений является общим: он пригоден, например, и для функции

x = a₀ + a₁ t + a₂ t² + a₃ t³ + …+ a_n tⁿ.

Естественно, что здесь получится система из n+1 нормальных уравнений для определения величин a₀, a₁, a₂, ..., a_n.

Рассмотрим частный случай применения метода наименьших квадратов. Пусть из теории известно, что

есть величина постоянная и ее нужно определить по опытным данным

(Рис. 7.10).

Систему уравнений для k можно записать так:

……….

Для получения нормального уравнения умножим каждое из этих уравнений на коэффициент при неизвестной k, т. е. на 1, и сложим полученные уравнения

,

отсюда

.

Следовательно, среднее арифметическое, полученное из опытных отношений x_i / t_i, дает решение поставленной задачи по методу наименьших квадратов. Это важное свойство средней арифметической объясняет ее широкое применение в практике обработки опытных данных.

Рассмотрим конкретный пример, вновь обратившись к заданному временному ряду.

Составим вспомогательную таблицу (табл. 7.5):

Таблица 7.5
ti	xi	ti xi	ti2
1	12	12	1
2	8	16	4
3	6	18	9
4	10	40	16
5	11	55	25
6	9	54	36
7	5	35	49

В этом случае система уравнений (нормальные уравнения) для отыскания a и b записыва­ется в следующем виде:

2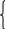 8а + 7b = 61

140а + 28b = 230. (7.9)

Решая систему, получаем:

a = − 14 / 28 = − 0,5; b = 300 / 28 10,7.

Тем самым х = − 0,5t + 10,7 – уравнение искомого тренда.

Нетрудно убедиться, что, подставив соответствующие значения сумм из вспомогательной таблицы в (7.8), значения для a и b получатся те же самые:

а = = = − − 0,5;

b = = 10,7.

Таким образом, коэффициенты a и b можно получить, подставляя значения сумм в решение нормальных уравнений в общем виде (7.8), или составляя нормальные уравнения подобно (7.9) с численными множителями, т. е. значениями сумм из вспомогательной таблицы, при неизвестных a и b. Расчет показателя на следующий день проводится так:

f₈ = − 0,5 · 8 + 10,7 = − 4 + 10,7 = 6,7

(см. рис. 7.11).

Замечание. Точность прогноза можно оценить при помощи стандартного отклонения или дисперсии. Стандартное отклонение определяется по формуле:

. (7.10)

Среднеквадратическое отклонение вычисляется по формуле:

. (7.11)

В этих формулах:

 −стандарт или стандартное отклонение, несмещенная оценка среднеквадратического отклонения случайной величины X относительно её математического ожидания;  — дисперсия;  − i−й элемент выборки;  − среднее арифметическое выборки;  — объём выборки.

Следует отметить отличие стандартного отклонения (в знаменателе стоит n −1) от корня из дисперсии (среднеквадратического отклонения) (в знаменателе − n). При малом объеме выборки оценка дисперсии через последнюю величину является несколько смещенной, при бесконечно большом объеме выборки разница между этими величинами исчезает.

Можно также точность прогноза оценить при помощи коэффи­циента корреляции:

. (7.12)

Если коэффициент корреляции r_n =1, то x_i = at_i+b, если r_n = −1, то x_i=−at_i+b. Таким образом, близость коэффициента корреляции к 1 (по абсолютной величине) говорит о достаточно тесной линейной связи.

Рис. 7.11
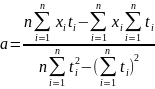