5. Математические модели в финансовых операциях

Переход к рыночной модели экономики обусловил повышение интереса к сфере финансов. С появлением частных предприятий и ростом их числа увеличивается и количество людей, заинтересованных в правильном ведении финансовых подсчетов. Однако не все заинтересованные лица могут произвести необходимые финансовые расчеты, особенно в тех случаях, когда анализируются платежи, разнесенные во времени или представляющие собой последовательность регулярно повторяющихся выплат. Сравнительно недавно понятия векселя, акции и других ценных бумаг вернулись в широкое употребление. Однако пока еще большинство людей мало информировано о разнообразных формах получения процентных денег. Работая в сфере управления предприятиями различного профиля, специалистам, так или иначе, придется сталкиваться с финансовыми документами и, соответственно, с финансовыми операциями. Поэтому представляется целесообразным рассмотреть математические модели в финансовых операциях.

Участники любой финансовой операции заранее оговаривают её условия. К таким условиям относятся: сумма кредита, займа или инвестиций, цена товара, сроки и способы начисления процентов, погашения долга, сроки и порядок инвестирования финансовых средств, и соответственно сроки и порядок погашения инвестиций и т. д.

Влияние на исход финансовой операции одновременно многих факторов делает ее результат неочевидным. Необходимо провести детальные расчеты, чтобы оценить количественно исход финансовой операции. Знакомство с математическими моделями, позволяющими проделать такой анализ, и составляет предмет этой главы. Количественный финансовый анализ имеет целью решение широкого круга задач: от элементарного начисления процентов до анализа сложных кредитных и коммерческих операций. К этим задачам можно отнести:

• измерение конечных финансовых результатов операций для каждой из участвующих в ней сторон;

• сравнение эффективности различных операций;

• выявление зависимости конечных результатов от основных параметров операции, сделки, контракта;

• разработку планов выполнения финансовых операций;

• расчет параметров эквивалентного изменения условий контракта.

В настоящей главе рассматриваются основные понятия, которыми оперируют в финансовых вычислениях: процент, ставка процента, учетная ставка, современная (текущая) стоимость платежа, методы наращения и дисконтирования платежей, принципы, лежащие в основе финансовых вычислений, современная практика расчетов.

5.1. Простые проценты. Сложные проценты

Денежные суммы обязательно привязывают к некоторым конкретным моментам или интервалам времени. Для этого в контрактах фиксируются соответствующие сроки, даты, периодичность поступления денежных средств, их выплат.

Время играет в финансовых операциях никак не меньшую роль, чем сами размеры денежных сумм. Необходимость учитывать фактор времени диктуется принципом неравноценности денег, относящихся к различным моментам времени, так как даже при отсутствии инфляции и риска одна тысяча рублей, полученная через год, не равноценна этой же сумме, поступившей сегодня. Неравноценность объясняется тем, что теоретически любая сумма денег может быть инвестирована в коммерческое предприятие и, соответственно, принести доход. Поступившие доходы могут в свою очередь быть реинвестированы и вновь принести доход и т. д. Поэтому сегодняшние деньги несут в себе большую ценность, чем будущие, а будущие поступления мене ценны, чем сегодняшние.

Следствием принципа неравноценности денег является неправомерность суммирования денежных величин, относящихся к разным моментам времени. Такое суммирование допустимо лишь в том случае, когда временной фактор не имеет значения, например в бухгалтерском учете для получения итогов по периодам и в финансовом контроле.

Учет фактора времени при проведении финансовых операций осуществляется с помощью методов наращения и дисконтирования, в основу которых положена техника процентных вычислений. С помощью этих методов осуществляется приведение денежных сумм, относящихся к различным временным периодам, к требуемому моменту времени в настоящем или будущем. При этом в качестве нормы приведения используется процентная ставка.

Процентная ставка. Под процентными деньгами или процентами в финансовых расчетах понимают абсолютную величину дохода, получаемого от предоставления денег в долг в любой форме: в виде выдачи денежной ссуды, продажи в кредит, помещения денег на сберегательный счет, учета векселя, покупки сберегательного сертификата или облигаций и т. д.

При заключении кредитного соглашения стороны (кредитор и заемщик) договариваются о размере процентной ставки – отношении суммы процентных денег, выплачиваемых за фиксированный период времени, к величине ссуды. Интервал времени, к которому относится процентная ставка, называется периодом начисления. Ставка измеряется в процентах либо представляется в виде десятичной или натуральной дроби.

Проценты начисляются, как правило, дискретно, т. е. в отдельные моменты времени. В качестве периодов начисления принимают год, полугодие, квартал, месяц. Иногда практикуют ежедневное начисление, а в ряде случаев удобно применять непрерывные проценты.

Проценты или выплачиваются кредитору по мере их начисления, или присоединяются к сумме долга. Процесс увеличения суммы денег в связи с присоединением процентов к сумме долга называется наращением.

В количественном финансовом анализе процентная ставка применяется не только как инструмент наращивания суммы долга, но и в более широком смысле – как измеритель степени доходности финансовой операции.

Существуют различные способы начисления процентов, зависящие от условий контракта. Разумеется, используют и различные виды процентных ставок, одно из основных различий между которыми связано с выбором исходной суммы для начисления процентов. Ставки процентов могут применяться к одной и той же начальной сумме на протяжении всего срока ссуды или к сумме с начисленными в предыдущем периоде процентами. В первом случае они называются простыми, во втором – сложными процентными ставками.

Процентные ставки, указываемые в контрактах, могут быть постоянными или переменными («плавающими»). Во втором случае значение ставки равно сумме некоторой изменяющейся во времени базовой величины и надбавки к ней, которую называют маржой. Размер маржи определяется рядом условий, например сроком операции. Обычно маржа находится в пределах 0,5−5 %.

Рассмотрим методы анализа сделок, в которых предусматриваются разовые платежи при выдаче и погашении кредита или депозита. Задачи такого анализа сводятся к расчету наращенной суммы, суммы процентов и размера дисконта, современной величины (текущей стоимости) платежа, который будет произведен в будущем.

Формула наращения по простым процентам. Под наращенной суммой ссуды (долга, депозита и т. д.) понимается ее первоначальная сумма вместе с начисленными на нее процентами к концу срока.

Пусть x₀ – первоначальная сумма денег, p – ставка простых процентов (в процентах). Начисленные проценты за один период равны x₀ · p / 100, а за k периодов − x₀ · k · p / 100.

Процесс изменения суммы долга с начисленными простыми процентами можно представить в виде арифметической прогрессии, членами которой являются величины:

x₀, x₀ + x₀ · p / 100 = x₀(1 + p / 100), x₀(1 + p / 100) + x₀ · p / 100 = x₀(1 + 2p / 100),…, x₀(1 + k p / 100).

Первый член этой прогрессии равен x₀, разность − x₀ · p / 100 , тогда последний член является наращенной суммой:

x_k = x₀ (1+ k p / 100) = x₀ (1+ k i), (5.1)

где i = p / 100, т. е. процентная ставка, выраженная десятичной дробью.

Формула (5.1) называется формулой наращения по простым процентам, или формулой простых процентов, а множитель

1 + k p / 100 = 1+ k i

в этой формуле – множителем наращения. Он показывает, во сколько раз наращенная сумма больше первоначальной суммы. Наращенную сумму можно представить в виде двух слагаемых: первоначальной суммы x₀ и суммы процентов I:

x_k = x₀ + I , (5.2)

где

I = x₀ · k · i. (5.3)

Процесс роста наращенной суммы по простым процентам показан графически на рис. 5.1. При начислении простых процентов по ставке p за базу берется первоначальная сумма долга. Наращенная сумма x_k изменяется линейно в зависимости от времени.

сумма

xk x0 время 1 k x0 k i x0 i

Рис. 5.1

Пример 5.1. Определить сумму процентов и накопленного долга, если ссуда 140 тыс. руб. взята на полгода при ставке простых процентов, равной 10 % годовых.

Решение.

I = x₀ · k · p / 100 = 140 · 0,5 · 10 /100 = 7 (тыс. руб.)

x_k = x₀ + I = 140 + 7 = 147 (тыс. руб.)

Сумма процентов составляет 7 тыс. руб., сумма накопленного долга – 147 тыс. руб.

Начисление простых процентов. Начисление простых процентов обычно используется в двух случаях: при заключении краткосрочных контрактов (предоставлении краткосрочных кредитов и т. п.), срок действия которых не превышает одного года, и когда проценты не присоединяются к сумме долга и выплачиваются периодически.

Ставка процентов обычно устанавливается на год. На практике же продолжительность краткосрочной операции обычно меньше года. В этом случае срок проведения операции корректируется следующим образом: величину k выражают в виде дроби

k = t / K, (5.4)

где k – срок ссуды в долях года; K – число дней и году (временная база); t - срок ссуды в днях.

В таком случае наращенная сумма вычисляется по формуле

x_k = x₀ (1+ t∙p / K∙100) = x₀ (1+ i∙t / K ). (5.5)

На практике применяются несколько вариантов расчета процентов, различающихся временной базой K и способом измерения срока пользования ссудой.

В процессе анализа в качестве временной базы К часто удобно использовать условный или финансовый год, состоящий из 360 дней (12 месяцев по 30 дней в каждом). Исчисляемые по такой базе проценты называют обыкновенными, или коммерческими процентами. Точные проценты получают, когда за базу берут действительное число дней в году: 365 или 366 (если год високосный).

Число дней пользования ссудой также может быть точным или приближенным.

В первом случае вычисляется фактическое количество дней между двумя датами, во втором – продолжительность ссуды определяют по количеству месяцев и дней ссуды, считая все месяцы равными и содержащими по 30 дней. В обоих случаях дата выдачи и дата погашения ссуды считаются за один день. Точное число дней между двумя датами можно подсчитать самостоятельно, либо прямым подсчетом, либо при помощи делового календаря, содержащего порядковые номера недель в году, или с помощью специальной таблицы, в которой представлены порядковые номера дат в году (см. приложение 1).

Различные варианты временной базы и методов подсчета количества дней ссуды приводят к следующим применяемым на практике схемам расчета процентов:

• точные проценты с точным числом дней ссуды (британская схема 365/365, когда в году считается 365 дней, полугодие приравнивается к 182 дням и берется точная длительность месяцев). Используется в Великобритании, США, Португалии;

• обыкновенные проценты с точным числом дней ссуды (французская схема 365/360, год принимается равным 360 дням (финансовый год) и учитывается точная длительность месяцев), используется во Франции, Бельгии, Испании;

• обыкновенные проценты с приближенным числом дней ссуды (германская схема 360/360, считается, что в году 360 дней, а в каждом месяце 30 дней). Используется в Германии, России, США.

Обыкновенные проценты (360/360) более удобно использовать в аналитических расчетах. Этим объясняется популярность их применения на практике в большинстве развитых стран, включая США и государства континентальной Европы.

В России применяются как обыкновенные (360/360), так и точные проценты (365/365). В частности, точные проценты используются в официальных методиках ЦБР и МФ РФ для расчета доходности по государственным обязательствам. Обыкновенные проценты в России используются в основном при проведении операций с векселями.

Поскольку точное число дней ссуды, как правило, больше приближенного, проценты с точным числом дней обычно выше, чем с приближенным.

Вариант расчета с точными процентами и приближенным измерением времени ссуды не применяется.

Точное и приближенное число дней для обыкновенных процентов связаны следующими зависимостями:

p₃₆₀ = 0,986301· p₃₆₅; p₃₆₅ = 1,013889· p₃₆₀.

Пример 5.2. Найти точное и приближенное число дней между 5 марта и 21сентября.

Решение. По таблице в приложении 1 находим, что 21 сентября является 264-м днем года, а 5 марта – 64-м днем. Поэтому точное число дней будет:

264 – 64 = 200 (дней).

Приближенное количество дней определится следующим образом. Количество полных месяцев (по 30 дней в месяце) в заданном сроке равно 5. Имеем:

5 · 30 + (30 – 5) + 21 = 195 (дней).

Ответ: между 5 марта и 28 сентября точное количество дней - 200, приближенное – 196 дней.

Пример 5.3. Ссуда в размере 5000 руб. положена в банк под 10 % годовых с 7 апреля по 15 ноября следующего года (год не високосный). Определить тремя способами наращенную сумму. Какой вариант наращения выгоден банку, а какой – вкладчику?

Решение. Наращенную сумму найдем по формуле (5.5). Возможны три варианта расчета:

1. Точные проценты с точным числом дней ссуды. По таблице в приложении: 7 апреля – это 97-й день года, 15 ноября – 319-й день. Точное количество дней, на которые положена ссуда в банк:

(365 – 97) + 319 = 587 (дней).

Временная база – 365 дней. Имеем:

x₁ = 5000 (1+ 587 ∙ 10 / 365 ∙ 100) = 5804,11 (руб.)

2. Обыкновенные проценты с точным числом дней ссуды. Точное количество дней – 587, временная база – 360 дней, тогда:

x₁ = 5000 (1+ 587 ∙ 10 / 360 ∙ 100) = 5815,28 (руб.)

3. Обыкновенные проценты с приближенным числом дней ссуды. Полных месяцев в сроке ссуды – 17. Приближенное количество дней:

18 · 30 + (30 – 7) + 15 = 578 (дней).

Временная база – 360 дней, тогда:

x₁ = 5000 (1+ 578 ∙ 10 / 360 ∙ 100) = 5802,78 (руб.).

Следовательно, банку выгоден третий вариант, а вкладчику – второй.

Простые переменные ставки. Процентные ставки не всегда остаются неизменными во времени, иногда в кредитных соглашениях предусматриваются дискретно изменяющиеся процентные ставки. В этом случае формула расчета наращенной суммы приобретает следующий вид:

x_k = x₀ (1+ k₁ ∙ i₁ + k₂ ∙ i₂ +…+ k_n ∙ i_n) = x₀ (1+ ), (5.6)

где x₀ – первоначальная сумма (ссуда), n – количество периодов начислений, i_i = p_i / 100 – ставка простых процентов в периоде с номером i, i=1,2,… n, k_i – продолжительность периода начисления процентов по ставке i_i.

Пример 5.4. В договоре, рассчитанном на год, ставка простых процентов на 1 квартал установлена в размере 9,5 % годовых, а на каждый из последующих кварталов – на 0,5 % меньше, чем в предыдущем. Определить множитель наращения К_нар. за весь срок договора.

Решение. Множитель наращения К_нар. вычисляется по формуле (5.6);

К_нар. = 1+ = 1 + 0,25∙ 9,5 / 100 + 0,25∙ 9 / 100 + 0,25∙ 8,5 / 100 + 0,25∙ 8 / 100 = 1 + 0,25 (9,5+9+8,5+8)/100 = 1,0875.

Таким образом, множитель наращения равен 1,0875.

Реинвестирование по простым процентам. Сумма депозита, полученная в конце обозначенного периода вместе с начисленными на нее процентами, может быть вновь инвестирована под ту же или другую процентную ставку. Процесс реинвестирования может повторяться неоднократно в пределах расчетного срока N. В случае многократного инвестирования в краткосрочные депозиты и применения простой процентной ставки наращенная сумма для всего срока N находится по формуле

x_k = x₀ (1+ k₁ ∙ i₁)(1+ k₂ ∙ i₂)…(1+ k_n ∙ i_n) = x₀ ). (5.7)

где k_t , t = 1,2…n – продолжительность последовательных периодов реинвестирования, связанных соотношением N = ; i_t , t = 1,2…n – ставки, по которым производится реинвестирование.

Пример 5.5. На сумму 150 тыс. руб. начисляются 10 % годовых. Проценты простые, точные (год не високосный). Определить наращенную сумму в двух случаях: если реинвестирование производится за 1 квартал ежемесячно и если реинвестирование не проводится.

Решение. Вычислим наращенную сумму при реинвестировании:

x_k = 150 (1+ 0,1·31/365)(1+0,1·28/365)(1+ 0,1·31/365) = 153,729 ( тыс. руб.).

Теперь определим наращенную сумму при отсутствии реинвестирования:

x_k = 150 (1+ 0,1·90/365) = 153,699 (тыс. руб.).

Таким образом, легко видеть, что реинвестирование увеличивает наращенную сумму.

Дисконтирование и учет. На практике часто приходится решать задачу, обратную наращению процентов, когда по данной сумме x_k , соответствующей моменту окончания финансовой операции, требуется найти исходную сумму x₀. Расчет x₀ по x_k называют дисконтированием суммы x_k . В зависимости от вида процентной ставки, при анализе краткосрочных финансовых операций применяют два метода дисконтирования – математическое и коммерческое

(т н банковский учет). В первом случае в качестве нормы приведения используют ставку i, применяемую при наращении. Во втором случае в роли нормы приведения выступает т н учетная ставка, для обозначения которой в дальнейшем будет использоваться символ d.

Величина x₀, найденная по x_k, называется современной величиной или текущей стоимостью суммы x_k.

Проценты в виде разности D = x_k x₀ называются дисконтом или скидкой. Дисконт как скидка с конечной суммы долга может определяться через процентную ставку или в виде абсолютной величины.

Процесс начисления и удержания процентов вперед называют учетом. На практике используют два принципа расчета процентов: путем наращения суммы ссуды и устанавливая скидку с конечной суммы долга. Чаще всего фактор времени учитывается в финансовых контрактах именно с помощью дисконтирования. Величина x₀ эквивалентна сумме x_k в том смысле, что через определенный период времени и при заданной ставке процентов эта величина в результате наращения станет равной x_k. Поэтому операцию дисконтирования называют также приведением. Однако понятие приведения несколько шире, чем дисконтирование. Приведение – это определение любой стоимостной величины на некоторый момент времени. Если некоторая сумма приводится к более ранней дате, чем текущая, то применяется дисконтирование, а если – к более поздней дате, то наращение. Схематически наращение и дисконтирование можно представить следующим образом:

НАСТОЯЩЕЕ		БУДУЩЕЕ
Исходная сумма Ставка		Наращенная сумма
Приведенная сумма		Возвращаемая сумма Ставка

Как уже упоминалось, существуют два вида дисконтирования: математическое дисконтирование и банковский (коммерческий) учет.

Математическое дисконтирование. Этот вид дисконтирования представляет собой решение задачи, обратной наращению первоначальной ссуды. Если в прямой задаче

x_k = x₀ (1+ k i),

то в обратной задаче −

x₀ = x_k / (1+ k i). (5.8)

Выражение 1 / (1+ k i) в формуле (5.8) называют дисконтным множителем. Он показывает, какую долю составляет первоначальная сумма ссуды в окончательной величине долга. Дисконт D суммы x_k равен

D = x_k − x₀ ,

при этом используемую норму приведения i называют декурсивной ставкой процентов.

Пример 5.6. Заемщик получил от банка кредит на 7 месяцев под 15 % простых годовых процентов с условием вернуть 500 тыс. руб. Какую сумму получил заемщик в момент заключения договора и чему равен дисконт?

Решение. По формуле (5.8) найдем сумму, которую получил заемщик в момент заключения договора:

x₀ = x_k / (1+ k i) = 500 /(1+ 0,15 · 7/12) = 459,770 (тыс. руб.).

При этом дисконт будет:

D = x_k − x₀ = 500 – 441,176 = 40,230 (тыс. руб.).

Таким образом, в момент заключения договора заемщик получил 459,770 тыс. руб., дисконт банка равен 40,230 тыс. руб.

Банковский (коммерческий учет). Операция учета, в том числе учета векселей, заключается в том, что банк до наступления срока платежа по векселю или иному платежному обязательству покупает его у владельца (являющегося кредитором) по цене ниже той суммы, которая должна быть выплачена по этому обязательству в конце срока, т. е. приобретает (учитывает) его с дисконтом.

Для расчета процентов при учете векселей применяется учетная ставка, которую обычно обозначают буквой d.

Простая годовая учетная ставка находится по формуле

d = (x_k x₀) / k x_k . (5.10)

Размер дисконта (учета), удерживаемого банком:

D = x_k – x₀ = d k x_k. (5.11)

Поэтому

x₀ = x_k − D = x_k − d k x_k = x_k (1 − d k ). (5.12)

Множитель 1 − d k называется дисконтным множителем. Срок k представляет собой период времени от момента учета векселя до даты его погашения в годах. При дисконтировании по учетной ставке чаще всего используют временную базу 360/360 или 365/360. Используемую при этом норму приведения d называют антисипативной ставкой процентов.

Пример 5.7. Владелец векселя на сумму 130 тыс. руб. со сроком уплаты 10 ноября учел его в банке 25 сентября по учетной ставке 9 % годовых. Определить сумму, полученную владельцем векселя, приняв K = 360 дней.

Решение. До погашения векселя осталось 45 дней (день погашения не учитывается). Сумма, полученная владельцем векселя, рассчитывается по формуле (5.12):

x₀ = x_k (1 − d k ) = 130 (1 − 0,09 ∙ 45 / 360) = 128,5375 (тыс. руб.).

Владелец векселя при учете его в банке получает 128,5375 тыс. руб.

Учетную ставку можно использовать для наращения, т. е. для расчета x_k по x₀. Из формулы (5.12) следует, что

x_k = x₀ / (1 − d k). (5.13)

Сравнение ставки наращения и учетной ставки. Операции дисконтирования и наращения по своей сути противоположны, однако ставки наращения и дисконтирования могут использоваться как для операции наращения, так и для операции дисконтирования. В этом случае в зависимости от применяемой ставки модно говорить о прямой и обратной задаче (табл. 5.1).

		Таблица 5.1
Ставка	Прямая задача	Обратная задача
Наращение i	Наращение: xk = x0 (1+ k i)	Дисконтирование: x0 = xk / (1+ k i)
Учетная d	Дисконтирование: x0 = xk (1 − d k )	Наращение: xk = x0 / (1 − d k)

Нетрудно заметить, что применение двух рассмотренных методов дисконтирования приводит к разным результатам, даже при i = d. Учетная ставка d дает более быстрый рост задолженности, чем обычная ставка i. Это легко проверяется простым расчетом коэффициентов наращения.

Найдем соотношения между процентной ставкой i и учетной ставкой d при условии, что в формулах (5.8) и (5.13) обеспечивается одинаковый коэффициент наращения. Приравняв выражения (5.8) и (5.13), имеем:

1+ k i = 1 / (1 − d k),

откуда

i = d / (1 − d k); (5.14)

d = i / (1 + k i). (5.15)

Совмещение начисления процентов по ставке наращения и дисконтирования по учетной ставке. В том случае, когда учету подлежит долговое обязательство, предусматривающее начисление простых процентов на первоначальную сумму долга, необходимо решить две задачи:

1. определить конечную сумму долга на момент его погашения;

2. рассчитать сумму, получаемую при учете, путем дисконтирования конечной суммы долга, применяя учетную ставку, действующую на момент учета.

Решение двух этих задач можно записать в виде одной формулы, содержащей наращение по ставке простых процентов, фигурирующей в долговом обязательстве, и дисконтирование по учетной ставке:

x₂ = x₁ (1+ k₁ i) (1 − k₂ d), (5.16)

где x₁ − первоначальная сумма ссуды; x₂ − сумма, получаемая при учете обязательства; k₁ − общий срок платежного обязательства, в течение которого начисляются проценты; k₂ − срок от момента учета до момента погашения долга. Эту ситуацию можно проиллюстрировать следующей схемой. Стрелки на схеме символизируют отсчет времени.

Исходная сумма x1	Период k1	Наращенная сумма xk1 = x1 (1+ k1 i)
	Период k2	Сумма при учете x2 = xk1 (1 − k2 d)

На момент погашения сумма долга через период времени k₁ составляла бы величину x_k1. Сумма, получаемая при учете, x₂, получается умножением суммы x_k1 на дисконтный множитель (1 − k₂ d), соответствующий периоду времени k₂, естественно меньшему, чем k₁.

Пример 5.8. Платежное обязательство уплатить через 90 дней 220 тыс. руб. с процентами, начисленными по ставке простых процентов p = 20 % годовых, было учтено за 20 дней до срока погашения по учетной ставке 16 % . Определить сумму, получаемую при учете.

Решение. По формуле (5.16) имеем:

x₂ = 220 (1 + 0,2 ∙90 / 365) (1 − 0,16 ∙20 / 360) = 228,7973 (тыс. руб.)

Владелец платежного обязательства получит при учете 228,7973 тыс. руб. Напомним, что в операциях учета, как правило, используют понятие финансового года, т. е. 12 месяцев по 30 дней. Заметим, что получи владелец документа долг с должника полностью (соответствует наращенной сумме за 90 дней), сумма была бы несколько большей – 230,8493 тыс. руб. Иными словами, банк оказывается в выигрыше. В этом и заключается интерес банка в такого рода операциях.

Определение продолжительности ссуды. Иногда ставится задача по нахождению временного интервала, за который исходная сумма при заданной ставке процентов вырастет до нужной величины, или по определению срока, обеспечивающего определенный дисконт с заданной величиной.

При использовании простой ставки наращения из (5.1) находим:

k = x_k − x₀ / x₀ i , (5.17)

где k − срок операции в годах.

При использовании учетной ставки d из (5.10) имеем:

k = x_k − x₀ / d x_k , (5.18)

где k − срок, оставшийся от момента учета до момента погашения долга в годах.

Оба выражения (5.17) и (5.18) определяют временной срок в годах, в то время как простые ставки применяются в основном в краткосрочных операциях, когда срок исчисляется днями. В этом случае срок финансовой операции в днях вычисляется, согласно (5.4) как

t = k ∙ K , (5.19)

где K − временная база.

Определение процентной ставки. Величина процентной ставки является мерой доходности финансовой операции, критерием сопоставления альтернатив и выбора наиболее выгодных условий. Из формул (5.1), (5.5), (5.13)

i = x_k − x₀ / x₀ ∙ k; (5.20)

i = K (x_k − x₀ ) /x₀ ∙ t ; (5.21)

d = (x_k − x₀ ) / x_k ∙ k; (5.22)

d = K (x_k − x₀ )/ x_k ∙ t . (5.23)

Напомним еще раз, что срок k в этих формулах имеет разный смысл: в (5.20) и (5.21) это весь срок финансовой операции, а в (5.22) и (5.23) − это срок, оставшийся от момента учета долгового обязательства до момента его погашения.

Пример 5.9. Определить доходность операции для кредитора, если он предоставил ссуду в размере 170 тыс. руб. на 80 дней и контрактом предусмотрена сумма погашения долга, равная 180 тыс. руб. Доходность выразить в виде простой ставки процентов i и учетной ставки d. Временную базу K принять равной 360 дням.

Решение. По формуле (5.21) определяем доходность операции в виде простой ставки процентов:

i = K (x_k − x₀ ) /x₀ ∙ t = 360 ∙ (180 − 170) / 170 ∙ 80 0,265.

По формуле (5.23) определим доходность операции в виде простой учетной ставки:

d = K (x_k − x₀ )/ x_k ∙ t = 360 ∙ (180 − 170) / 180 ∙ 80 0,25.

Итак, доходность операции, выраженная в виде простой процентной ставки, составляет примерно 26,5 %, а виде простой учетной ставки – 25 %. Заметим еще раз, что цифры в ответе говорят о том, что наращение суммы по простой учетной ставке происходит быстрее, чем по простой процентной ставке.

Сложные проценты

В отличие от простых процентов, применяемых при краткосрочных финансовых операциях (до одного года), сложные проценты применяются в долгосрочных финансово-кредитных операциях, если проценты не выплачиваются периодически сразу после их начисления за прошедший интервал времени, а присоединяются к сумме долга. Присоединение начисленных процентов к сумме, которая служила базой для их определения, иногда называют капитализацией процентов.

Формула наращения по сложным процентам. Проценты на капитал можно рассматривать как награду, которую получает кредитор от заемщика за пользование капиталом, при­надлежащим кредитору.

Предположим, что заемщик кладет в банк, выплачивающий p % годовых (процентную ставку), некоторую сумму денег, которую мы для определенности, как и раньше, обозначим через x₀.

Это означает, что ровно через год у заемщика на счету будет сум­ма, равная

x₁ = x₀ + x₀ · p / 100 = x₀ (1+ i ),

а еще через год —

x₂ = x₁ + x₁ · i = x₁ (1+ i) = x₀ (1+ i) ².

Терпеливый заемщик через k лет станет обладателем суммы, рав­ной

x_k = x₀ (1+ p / 100) ^k = x₀ (1+ i) ^k . (5.24)

Здесь x_k − наращенная сумма, i − годовая ставка сложных процентов, k − срок ссуды, (1+ i) ^k − множитель (коэффициент) наращения, который обозначим К_нар..

На практике в большинстве случаев применяют дискретные проценты, т. е. проценты, начисляемые за одинаковые интервалы времени (год, полугодие, квартал и т. д.).

Наращение по сложным процентам представляет собой рост по закону геометрической прогрессии, первый член которой равен x₀ , а знаменатель –

1 + i.

Сравним коэффициенты наращения по простым и сложным процентам по ставке 10 % годовых и временной базе 360 дней. Результаты расчетов представлены в табл. 5.2.

				Таблица 5.2
Коэффициент наращения	30 дней	180 дней	1 год	5 лет	10 лет
(1+ k i)	1,008	1,050	1,1	1,5000	2,0000
(1+ i) k	1,008	1,049	1,1	1,6105	2,5937

Отметим, что при сроке операции менее года наращение по простым процентам дает больший результат, чем по сложным процентам, а при сроке более года – наоборот. Этим и объясняется тот факт, что при сроке финансово-кредитной операции менее года обычно применяются простые процентные ставки, а при сроке более года – сложные процентные ставки.

Графически изменения коэффициента наращения по простым и по сложным процентам представлены на рис. 5.2.

Кнар. k 1 x0

Рис. 5.2

Если ставка сложных процентов меняется во времени, то формула наращения принимает вид:

x_k = x₀ (1+ i₁) ^k₁ (1+ i₂) ^k₂... (1+ i_n) ^k_n , (5.25)

где i₁, i₂,… i_n − последовательные значения ставок процентов, действующих в периоды k₁, k₂,… k_n соответственно.

В этом случае выражение (1+ i₁) ^k₁ (1+ i₂) ^k₂... (1+ i_n) ^k_n является множителем наращения К_нар..

Пример 5.10. В договоре зафиксирована переменная ставка сложных процентов, определяемая как 10 % годовых, плюс переменная маржа: 5 % в первые два года, 7 % в третий год и 10 % в четвертый год. Определить величину множителя наращения за четыре года.

Решение. Множитель наращения находится по формуле (5.25):

К_нар. = (1 + 0,15)²(1 + 0,17) (1 + 0,2) 1,86.

Множитель наращения за четыре года составляет 1,86.

Формулы удвоения суммы. Для оценки результатов сделки кредитору и заемщику необходимо знать, через сколько лет сумма ссуды возрастет в N раз при заданной процентной ставке. Чтобы выяснить этот вопрос приравняем множитель наращения к величине N, в результате получим:

а) для простых процентов 1 + k i_прост. = N, тогда

k = (N −1) / i_прост. ; (5.26)

б) для сложных процентов (1 + i _сложн.) ^k = N, тогда

k = lnN / ln(1 + i _сложн.). (5.27)

При N = 2 формулы (5.26) и (5.27) называют формулами удвоения. Они принимают соответственно вид:

а) для простых процентов:

k = 1 / i_прост. ; (5.28)

б) для сложных процентов:

k = ln 2 / ln (1 + i _сложн.) = 0,693/ ln (1 + i _сложн.). (5.29)

Вычисления с логарифмами довольно трудоемки, поэтому для быстрой оценки величины k в (5.29) на практике иногда пользуются приближенным расчетом, известным как «правило 72». Правило заключается в следующем: если i − процентная ставка, выраженная в процентах, то 72/ i представляет собой число периодов, за которое приблизительно исходная сумма удвоится. Это правило дает неплохие результаты для небольших значений i. Так, например, если годовая ставка сложных процентов I = 6 %, то применение «правила 72» дает значение k = 12 лет, по формуле (5.29) с округлением до трех знаков после запятой k 6,116 года, что весьма и весьма неплохо. Если годовая ставка сложных процентов I = 12 %, то применение «правила 72» дает значение k = 6 лет, по формуле (5.29) с округлением до трех знаков после запятой k 11,895 года, что вполне допустимо для ориентировочных расчетов.

Следует отметить, что в большинстве финансовых расчетов процентная ставка берется в десятичных дробях, а при расчете по «правилу 72» используется i, выраженная в процентах.

Пример 5.11. Рассчитать за сколько лет долг увеличится вдвое при трех различных ставках простых и сложных процентов, равных 2 %, 3 % и 5 % годовых. Для ставки сложных процентов расчеты выполнить по точной и приближенной формулам. Сравнить результаты.

Решение. Для случая простых процентов расчеты проведем по формуле (5.28):

а. k = 1 / i_прост = 1 / 0,02 = 50 лет,

б. k = 1 / 0,03 = 33,33 лет,

в. k = 1 / 0,05 = 20 лет

Для сложных процентов по точной формуле (5.29) получим:

а. k = ln 2 / ln (1 + i _сложн.) = ln 2 / ln (1,02) 35 лет,

б. k = ln 2 / ln (1,03) 23,45 года,

в. k = ln 2 / ln (1,05) 14,2 года.

Для сложных процентов по приближенной формуле:

а. k = 72 / 2 = 36 лет,

б. k = 72 / 3 = 24 года,

в. k = 72 / 5 = 14,4 года.

.

Одинаковое значение ставок простых и сложных процентов приводит к разным результатам. При малых значениях ставки сложных процентов точная и приближенная формулы дают почти одинаковые результаты.

Остается вопрос, какие ставки считать малыми. Можно составить таблицу, в которой отражены результаты точных и приближенных вычислений сроков удвоения суммы в зависимости от процентной ставки. Можно вычислить отклонение приближенных вычислений от точных в процентах. Оказывается, что минимальное отклонение наблюдается при ставке 8 % . При этом отклонение приближенных вычислений составляет 0,1 %. При ставке 20 %, отклонение приближенных вычислений начинает превышать 5 %. Можно значение сложной процентной ставки 20 % принять за границу малых значений. Иными словами, при значениях сложных процентных ставок менее

20 % погрешность приближенных вычислений срока удвоения суммы не превышает 5 %.

Начисление процентов при дробном числе лет. При дробном числе лет проценты начисляются разными способами:

1. по формуле сложных процентов:

x_k = x₀ (1+ i) ^k ;

2. на основе смешанного метода, согласно которому на целое число лет начисляются сложные проценты, а на дробное – простые;

x_k = x₀ (1+ i) ^a (1 + bi), (5.30)

где k = a + b; a − целое число лет, b − дробная часть года;

3. в ряде коммерческих банков применяется правило, в соответствии с которым за отрезки времени меньше периода начисления проценты не начисляются, т. е.

x_k = x₀ (1+ i). (5.31)

Поскольку b < 1, то, помня о том, что наращение по простым процентам при сроках операции менее года происходит быстрее, чем по сложным, имеем:

1 + bi > (1+ i) ^b .

Следовательно, наращенная сумма, вычисленная по формуле (5.30), будет больше суммы, вычисленной по формуле сложных процентов.

Пример 5.12. Банк предоставляет ссуду в размере 120 тыс. руб. на 33 месяца под 25 % сложных годовых на условиях ежегодного начисления процентов. Какую сумму предстоит вернуть заемщику банку по истечении срока ссуды? Расчет провести тремя способами. Проанализировать полученные результаты расчета.

Решение. Определим суммы, которые предстоит вернуть заемщику банку, тремя способами:

а. x_k1 = x₀ (1+ i) ^k = 120 (1 + 0,25)^2,75 221,658 (тыс. руб.);

б. x_k2 = x₀ (1+ i) ^a (1 + bi) = 120 (1 + 0,25)² (1 + 0,75∙0,25) 222,656 (тыс. руб.);

в. x_k3 = x₀ (1+ i) ^a = 120 (1 + 0,25)² = 187,500 (тыс. руб.).

Как следует из расчетов, третий вариант расчета выгоден заемщику, второй вариант расчета выгоден банку.

Номинальная ставка процентов. Пусть годовая ставка сложных процентов равна j, а число периодов начисления в году равно m, тогда каждый раз проценты начисляются по ставке j / m. Ставка j называется номинальной. Начисление процентов по номинальной ставке производится по формуле

x_k = x₀ (1+ j / m ) ^N, (5.32)

где N = mk – общее число периодов начисления.

Если срок ссуды измеряется дробным числом, то при разовом начислении процентов в году наращенную сумму можно рассчитывать несколькими способами, приводящими к разным результатам.

Пример 5.13. В банк вложены деньги в сумме 6 тыс. руб. на два года с полугодовым начислением сложных процентов по ставке 15 % годовых. Определить наращенную сумму и сравнить ее со случаем, когда проценты начисляются ежеквартально.

Решение. Определим наращенную сумму при полугодовом начислении процентов по формуле (5.32):

x_k = x₀ (1+ j / m ) ^mk = 6 · (1 + 0,15 / 2)⁴ 8,013 (тыс. руб.).

Если начисление процентов будет происходить ежеквартально, то к концу двух лет сумма составит:

x_k = 5 · (1 + 0,2 / 4)⁸ 8,055 (тыс. руб.).

Наращенная сумма при полугодовом начислении процентов составит к концу второго года 8,013 тыс. руб., а при ежеквартальном начислении − 8,055 тыс. руб.

Из решения примера можно сделать следующие выводы:

• чем чаще в течение года происходит начисление по сложным процентам, тем больше наращенная сумма;

• при начислении сложных процентов 12 % годовых не эквивалентно 1 % в месяц;

• для простых процентов эти выводы недействительны. Одно из характерных свойств наращения по простым процентам заключается в том, что наращенная сумма не зависит от частоты начисления простых процентов. Наращение по простым процентам по ставке 12 % годовых дает тот же результат, что и ежемесячное наращение по ставке 1 % в месяц;

• при наращении по сложным процентам ежемесячное начисление дает больший результат, чем наращение один раз в год.

Пример 5.14. Ссуда в размере 25 тыс. руб. предоставлена на 32 месяца. Номинальная ставка равна 50 % сложных процентов годовых. Начисление процентов ежеквартальное. Вычислить наращенную сумму в трех случаях:

• на дробную часть начисляются сложные проценты;

• на дробную часть начисляются простые проценты;

• дробная часть не учитывается.

Решение. Поскольку по условию задачи начисление процентов ежеквартальное, то по формуле (5.32) имеем: N = mk = 4 ·32/ 12 =32/3. Определим наращенную сумму, когда на дробную часть начисляются сложные проценты:

x_k = 25(1 + 0,5 / 4)^{32 / 3} 87,815 (тыс. руб.).

Определим наращенную сумму, когда на дробную часть начисляются простые проценты (целое число кварталов равно 10, дробное – 2/3):

x_k = 25(1 + 0,5 / 4)¹⁰ (1 + (0,5 /4) · 2/3) 87,948 (тыс. руб.).

Найдем наращенную сумму, когда учитывается только целая часть года:

x_k = 25(1 + 0,5 / 4) ¹⁰ 81,183 (тыс. руб.).

Наращенная сумма в заданных трех случаях будет 87,815 тыс. руб. в первом, 87,948 тыс. руб. во втором и 81,183 тыс. руб. в третьем случае.

Из результатов, полученных при решении задачи, следует, что наибольшего значения наращенная сумма достигает во втором случае, когда на дробную часть срока начисляются простые проценты, наименьшего – в третьем случае, когда учитывается только целая часть года. Такого результата следовало ожидать, поскольку наращение по простым процентам в промежутках времени меньше года, как мы помним из предшествующих выкладок, больше чем по сложным процентам.

Эффективная ставка. Эффективная ставка показывает, какая годовая ставка сложных процентов дает тот же финансовый результат, что и m – разовое наращение в год по ставке j / m. Если проценты начисляются по сложной ставке m раз в год, каждый раз по ставке j / m, то можно записать равенство для множителей наращения:

(1 + i_э) ^k = (1+ j / m ) ^mk, (5.33)

где i_э – эффективная ставка, а j – номинальная. Из (5.33) нетрудно получить выражение для i_э:

i_э = (1+ j / m ) ^m – 1. (5.34)

Заметим, что при m = 1 из (5.34) следует, что i_э = j.

Выражение для j имеет вид:

j = m ((1 + i_э) ^1/m – 1). (5.35)

Пример 5.15. Предприниматель может получить ссуду на условиях:

• ежемесячного начисления процентов из расчета 35 % годовых;

• полугодового начисления процентов из расчета 37 % годовых.

Какой вариант предпочтителен для предпринимателя?

Решение. Определим эффективную годовую ставку при ежемесячном и при полугодовом начислении процентов:

i_э = (1+ j / m ) ^m – 1= (1 + 0,35/12)¹² – 1 = 0,412;

i_э = (1+ j / m ) ^m – 1= (1 + 0,37/2)² – 1 = 0,4042.

Ответ: эффективная годовая ставка при ежемесячном начислении процентов равна 41,2 %, а при полугодовом начислении – 40,4 %. Второй вариант выгоднее.

Заметим, что эффективная ставка не зависит от величины кредита, а зависит только от номинальной ставки j и количества начислений в году m.

Понимание роли эффективной процентной ставки весьма важно для анализа финансовой деятельности предприятия. В рекламных проспектах обычно не говорится о природе процентной ставки, хотя в большинстве случаев речь идет о номинальной процентной ставке, которая может существенно отличаться от эффективной.

Пример 5.16. Определить какой должна быть номинальная ставка при ежемесячном начислении процентов, чтобы обеспечить эффективную ставку 15 % годовых.

Решение. По формуле (5.35) имеем:

j = m ((1 + i_э) ^1/m – 1) = 12 ((1 + 0,15)^1/12 – 1) = 0,1406.

Чтобы обеспечить эффективную ставку 15 % годовых, номинальная ставка при ежеквартальном начислении процентов должна быть 14,06 %.

Пример 5.17. Рассчитать эффективную годовую процентную ставку при различной частоте начисления процентов, если номинальная ставка составляет 15 %.

Решение. Результаты расчета эффективной годовой процентной ставки при различной частоте начисления процентов представлены в табл. 5.3.

					Таблица 5.3
m	1	2	4	12	365
iэ	0,15	0,1556	0,1587	0,1608	0,1618

Из таблицы видно, что при заданной j = 0,15, i_э j при различных частотах начисления (i_э = j, как уже отмечалось, только при m = 1).

Учет по сложной ставке процентов. Как и в случае с простыми процентами рассмотрим два вида учета: математический и банковский.

Математический учет. В этом случае решается задача, обратная наращению по сложным процентам. Запишем исходную формулу для наращения по сложным процентам

x_k = x₀ (1+ i) ^k

и из нее определим x₀:

x₀ = x_k / (1+ i) ^k = x_k υ ^k , (5.36)

где

υ ^k = 1 / (1+ i) ^k (5.37)

− учетный или дисконтный множитель.

Если проценты начисляются m раз в году, то

x₀ = x_k / (1+ j / m ) ^mk = x_k υ ^mk, (5.38)

где

υ^mk = 1 / (1+ j / m) ^mk (5.39)

− дисконтный множитель.

Величину x₀, полученную дисконтированием x_k, называют современной (текущей) стоимостью, или приведенной величиной x_k .

Суммы x₀ и x_k эквивалентны в том смысле, что платеж в сумме x_k через k лет равноценен сумме x₀, выплачиваемой в настоящий момент. Разность D = x_k − x₀ называют дисконтом.

Банковский учет. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле

x₀ = x_k (1 − d_сл.)^k, (5.40)

где d_сл. – сложная учетная ставка.

Дисконт в этом случае определяется по формуле

D = x_k − x₀ = x_k − x_k (1 − d_сл.)^k = x_k (1 − (1 − d_сл.)^k). (5.41)

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.

Пример 5.18. При рождении внука дедушка положил в банк на 18 лет под 5% годовых некоторую сумму. К моменту совершенноле­тия на счете оказалось 100 тыс. руб. Каким был первоначальный вклад?

Решение. По условию имеем:

x₁₈ = x₀ (1+ 0,05) ¹⁸ ,

где

x₁₈ = 100000 руб.

Можно записать

x₀ = 10000/ (1+ 0,05) ¹⁸= 41552 руб.

Иными словами, первоначальный вклад равен 41 тыс. 552 руб.

Каким будет ответ на поставленный вопрос, если предположить, что речь идет о наращении по банковской учетной ставке?

Запишем формулу (5.40):

x₀ = x_k (1 − d_сл.)^k = x₁₈ (1 − d_сл.)¹⁸ = 100000 (1 – 0,05)¹⁸ = 39721 руб.

Как видим, результат при использовании процентной и учетной ставки получился разный.

Номинальная и эффективная учетные ставки. В тех случаях, когда дисконтирование применяется m раз в году, используют номинальную учетную ставку f. Тогда в каждом периоде, равном 1 / m части года, дисконтирование осуществляется по сложной учетной ставке f / m. Процесс дисконтирования по этой сложной учетной ставке описывается формулой

x₀ = x_k (1− f / m ) ^N, (5.42)

где N – общее число периодов дисконтирования (N = mk).

Дисконтирование не один, а m раз в году быстрее снижает величину дисконта.

Под эффективной учетной ставкой понимают сложную годовую учетную ставку, эквивалентную (по финансовым результатам) номинальной, применяемой при заданном числе дисконтирований в году m раз.

В соответствии с определением эффективной учетной ставки найдем ее связь с номинальной учетной ставкой из равенства дисконтных множителей:

(1− f / m ) ^mk = (1 − d_сл.)^k,

откуда следует:

d_сл.= 1 − (1− f / m ) ^m . (5.43)

Из выражения (5.43) следует, что эффективная учетная ставка всегда меньше номинальной.

Наращение по сложной учетной ставке. Наращение является обратной задачей для учетных ставок. Формулы наращения по сложным учетным ставкам можно получить из формул дисконтирования (5.40) и (5.42):

x_k = x₀ / (1 − d_сл.) ^k ; (5.44)

x_k = x₀ / (1− f / m ) ^N . (5.45)

Пример 5.19. Какую сумму следует проставить в векселе, если выданная сумма равна 250 тыс. руб., срок погашения – 3 года. Вексель рассчитывается исходя из сложной годовой учетной ставки 15 %.

Решение. По формуле (5.44) определим сумму, которую следует проставить в векселе:

x_k = x₀ / (1 − d_сл.) ^k = 250 / (1 – 0,15)³ = 366,8529 (тыс. руб.).

В векселе следует проставить суму, равную 366,8529 тыс. руб.

Пример 5.20. Решить предыдущую задачу при условии, что наращение по сложной учетной ставке производится поквартально.

Решение. По формуле (5.45) имеем:

x_k = x₀ / (1− f / m ) ^N = 250 / (1− 0,15 / 4)^{3 · 4} = 360,3124 (тыс. руб.).

Если наращение по сложной учетной ставке производится поквартально, то в векселе следует проставить сумму 360,3124 тыс. руб.

Непрерывные проценты. Как было показано ранее, наращенная сумма при начислении дискретных процентов определяется по формуле

x_k = x₀ (1+ j / m ) ^mk ,

где j – общее номинальная ставка сложных процентов, m – число периодов начисления процентов в году.

Чем больше будет число периодов начисления в году m, тем меньше будут промежутки времени между моментами начисления процентов. При предельном переходе, устремив m → , будем иметь:

x_k = = x₀ .

Из теории пределов курса высшей математики известен второй замечательный предел: . Если положить n = m / j, то нетрудно прийти к следующему равенству:

= = ,

где e – основание натурального логарифма.

Сопоставляя полученное выражение с предыдущей формулой нетрудно получить:

x_k = x₀ . (5.46)

Чтобы отличать ставку дискретных процентов от ставки непрерывных процентов, ставку непрерывных процентов называют силой роста и обозначают буквой δ:

x_k = x₀ . (5.47)

Как видно из вывода формулы (5.46), сила роста представляет собой номинальную ставку процентов при m → . Дисконтирование на основе непрерывных процентных ставок осуществляется по формуле:

x₀ = x_k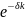 . (5.48)

Пример 5.21. На первоначальную сумму долга 10 тыс. руб. непрерывно начисляются проценты с силой роста 12 % в течение 15 лет. Определить наращенную сумму.

Решение. По формуле (5.47) получаем:

x_k = x₀ = 10 = 60,496 (тыс. руб.).

Итак, наращенная сумма составит 60,496 тыс. руб.

Связь дискретных и непрерывных процентных ставок. Формула эквивалентного перехода от дискретных ставок начисления процентов к непрерывным ставкам и наоборот может быть легко получена приравниванием соответствующих множителей наращения:

(1 + i)^k = .

Из этого равенства следует:

i = – 1; (5.49)

δ = 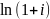. (5.50)

Пример 5.22. Годовая ставка сложных процентов равна 20 %. Чему равна эквивалентная сила роста?

Решение. По формуле (5.50) имеем:

δ = = =0,182.

Годовой ставке сложных процентов, равной 20 %, эквивалентна сила роста непрерывных процентных ставок 18,2 %.