9.2. Модель мобилизации

Под термином политическая, или социальная, мобилизация понимается вовлечение людей в партию или в число ее сторонников, в какое-либо общественное движение, религиозную группу и т. п.

Вследствие того что текущий уровень мобилизации тесно связан с прошлым ее уровнем, а будущая мобилизация зависит от сегодняш­них успехов пропагандистской кампании, ясно, что при построении соответствующей модели необходимо учитывать временной фактор. Иными словами, нужно понимать, что искомая модель должна быть динамической. От модели требуется отразить изменение уровня мобилизации в некотором регионе между двумя соседними моментами времени (за год, за месяц, неделю, день и т. п.).

Примем за единицу ту часть населения, для которой мобилизация рассматриваемого типа имеет смысл. Пусть x _n − доля мобилизованного ­ на­селения в момент времени t_n = n. Тогда доля немобилизованного населения будет равна 1 — x_n (рис. 9.6).

За месяц, например, уровень мобилизации может измениться по двум основ­ным причинам:

1) часть населения удалось привлечь дополнительно; ясно, что эта величина тем больше, чем выше доля еще не вовлеченного населения на момент t_n = n, и поэтому можно считать ее равной

α (1 − x_n)

(здесь 0 < α < 1 — коэффициент агитируемости, постоянный для дан­ного региона);

xn 1−xn

Рис.9.6

2) часть населения убыла (по разным причинам); ясно, что это уменьшает долю вовлеченного населения тем больше, чем выше была эта доля на момент t_n = n, и поэтому потери, связанные с выбытием, можно считать равными

β x_n

(здесь 0 < β < 1 — постоянный коэффициент выбытия).

Подчеркнем, что числовые параметры α и β отражают пропорци­ональное изменение интересов, взглядов и намерений соответствую­щих частей населения рассматриваемого региона.

Таким образом, изменение уровня мобилизации за единицу вре­мени

Δ x_n = x_n+1 − x_n

равно разности между долей населения, привлеченного дополни­тельно, и долей выбывшего сагитированного населения:

x_n+1 − x_n = α (1 − x_n) – β x_n. (9.12)

Это и есть модель процесса мобилизации.

Последнее соотношение легко преобразуется к следующему виду:

x_п+1 = α + γ x_n, (9.13)

где

γ = 1 — α — β.

Параметр γ не может быть больше 1 и меньше (−1) вследствие того, что исходные параметры α и β положительны и меньше единицы.

Полученное уравнение (9.13) называется линейным разностным уравнением с постоянными коэффициентами.

С уравнениями подобного рода читатель, несомненно, уже не раз сталкивался, правда, по большей части в простейших вариантах.

Один из них (при γ = 1) описывает правило, по которому ка­ждый член последовательности, начиная со второго, получается из предыдущего путем сложения с некоторым постоянным числом:

x_п+1 = α + x_n,

т. е. арифметическую прогрессию.

Второй (при α = 0) описывает правило, по которому каждый член последовательности, начиная со второго, получается из предыдуще­го путем умножения на некоторое постоянное число:

x_n+1 = γ x_n,

т. е. геометрическую прогрессию.

Предположим, что начальная доля привлеченного населения М₀ известна. Тогда, используя уравнение (9.10), нетрудно получить (для определенности считаем, что γ 1) следующие выражения:

x₁ = α + γ x₀,

x₂ = α + γ x₁ = α + γ (α + γ x₀) = α (1+ γ)+ γ² x₀,

x₃ = α + γ x₂ = α + γ (α (1+ γ ) + γ² x₀) = α (1+ γ+ γ²)+ γ³ x₀,

Продолжая рассуждения аналогичным образом, можно записать:

x_n = α (1+ γ + γ² +…+ γ^n-1)+ γⁿ x₀. (9.14)

Заметим, что выражение в скобках представляет собой геометрическую прогрессию со знаменателем γ. Как известно, сумма первых n членов геометрической прогрессии выражается формулой:

s_n = ,

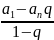где a₁ – первый член геометрической прогрессии, q – знаменатель прогрессии, a_n = a₁ q ^n-1. Применяя формулу (9.4) к геометрической прогрессии из (9.3), и, учитывая, что a₁ = 1, a_n = 1× γ^n-1 , q = γ , имеем:

1+ γ + γ² +…+ γ^n-1 = = . (9.15)

Окончательно приходим к выражению:

x_n = α + γⁿ x₀ . (9.16)

Попробуем проанализировать возможности построенной модели. Нас будет интересовать стационарная ситуация, когда количество вновь мобилизованных равно количеству выбывших. Положим в (9.13) x_п+1 = x_n, тогда

x_п = x_стац. = = . (9.17)

Так как α и β находятся в промежутке от 0 до 1, величина γ = 1 — α — β находится в промежутке от ( −1) до 1. При увеличении n величина x_п будет стремиться к стационарному значению x_стац.. Однако, если γ > 0, или говоря иначе, α + β < 1, то x_п стремится к стационарному состоянию монотонно. Если α + β > 1, то приближение будет в виде затухающих колебаний. На рис. 9.7 приведено семейство кривых, отвечающих условию: α = 0,03, β = 0,07 (при этих значениях α + β < 1). Уравнение 9.13 в этом случае запишется:

x_п+1 = 0,9 x_n + 0,03 (9.18)

Для принятых α и β значение x_стац. = 0,3. На рис. 9.7 приведено семейство кривых, построенное по (9.18) для различных значений x₀, приведенных на графике.

Рис.9.7

Все зависимости стремятся монотонно к стационарному значению 0,3. На рис. 9.8 приведена зависимость x_п от n для x₀ =0,3. В этой зависимости α выбрано равным 0,9, β – равным 0,6. Для этих величин x_стац. = 0,6. Уравнение

(9.13) запишется следующим образом:

x_п+1 = − 0,5 x_n + 0,9 (9.19)

Зависимость стремится к x_стац.= 0,9/1,5 = 0,6. По характеру зависимость напоминает затухающие колебания.

Рис.9.8

Интересно отметить, что построенная модель, несмотря на про­стоту подходов и рассуждений, довольно хорошо отражает реальные процессы. Так. предложенная модель мобилизации использовалась для изучении динамики числа голосов, поданных за демократиче­скую партию в Лейк Кантри (США) в 1920-1968 гг., и оказалось, что она достаточно хорошо описывает качественные характеристи­ки процесса мобилизации.