9.3. Модель гонки вооружений

Рассмотрим конфликтную ситуацию, в которой могут оказаться две соседние страны, для определенности названные странами X и Y.

Обозначим через x = x(t) расходы на вооружение страны X и че­рез y = y(t) расходы на вооружение страны Y в момент времени t 0.

Предположение 1

Страна X вооружается, опасаясь потенциальной угрозы войны со стороны страны Y, которая в свою очередь, зная о росте затрат на вооружение страны X, также увеличивает свои расходы на воору­жение. Каждая страна изменяет скорость роста (или сокращения) вооружений пропорционально уровню затрат другой. В простейшем случае это можно описать так:

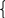
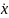= αу,

= βx, (9.20)

где α и β – положительные постоянные.

Однако написанные уравнения имеют очевидный недостаток — уровень вооружения ничем не лимитируется. Поэтому правые части этих уравнений нуждаются в естественной корректировке.

Предположение 2

Чем больше текущий уровень расходов страны на оборону, тем мень­ше скорость его роста. Это позволяет внести в предыдущую систему следующие изменения:

= αу − γx,

= βx − δy, (9.21)

где γ и δ – положительные постоянные.

Предположение 3

Каждая страна наращивает вооружение, руководствуясь своими державными притязаниями и враждебностью к соседней стране, даже если эта страна не угрожает существованию данной. Обозначим соответствующие претензии через а и b (а и b — положительные по­стоянные). В случае если постоянные а и b отрицательны, их можно назвать коэффициентами доброй воли.

Основываясь на всех трех предположениях, в результате получа­ем следующую систему уравнений:

= αу − γx + a,

= βx − δy + b. (9.22)

Модель гонки вооружений построена. Эту модель также называют моделью Ричардсона, по имени ее создателя.

Решением полученной системы являются функции x(t) и y(t), определяемые для данных начальных условий х₀ 0 и y₀ 0 (на­чального состояния гонки вооружений).

Проанализируем полученную систему, предполагая, что уровни затрат обеих стран на вооружение не зависят от времени (являются стационарными). Это означает, что

= 0, = 0,

или иначе:

αу − γx + a = 0

βx − δy + b = 0 (9.23)

Рассмотрим конкретный пример.

Пример 9.1. Пусть система уравнений гонки вооружений имеет следующий вид:

= 4у − 6x + 11,

= 4x − 5y + 9.

Если скорости изменения величин х и у равны нулю, то эти ве­личины с необходимостью связаны условиями:

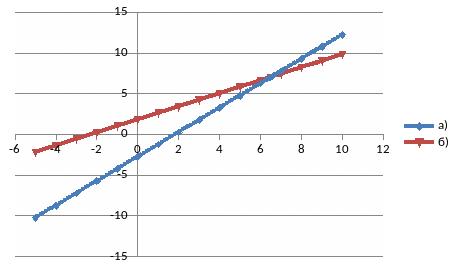
а). 4у − 6x + 11 = 0,

б). 4х − 5у + 9 = 0.

Каждое из этих уравнений описывает прямую на плоскости (х, у), и точка пересечения этих прямых

M* ( 6,5; 7)

лежит в первой четверти (рис. 9.9).

(+ +) (+) (−) (+) (− −) (−) I II III IV

Рис. 9.9

Прямая, заданная уравнением (а), разбивает плоскость, и началь­ная точка О (0,0) лежит в положительной полуплоскости. В рассма­триваемом примере то же справедливо и для прямой, заданной урав­нением (б) (рис. 9.9).

Так как всегда х 0 и у 0, то в анализе ситуации нас интересует первая четверть плоскости. Пересекающимися прямыми первая четверть разбивается на четыре области, которые удобно обозначить так:

I – (+,+), II – ( ,+), III – ( ), IV – (+, ),

(рис. 9.9). Пусть начальное состояние (х_о,у_о) находится в области I. Тогда будут выполнены неравенства

(а) : 4у₀ − 6x₀ + 11 0,

(б) : 4х₀ − 5у₀ + 9 0.

Из неравенств следует, что скорости и 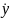в этой точке положительны и, значит, обе величины (х и у) должны возрастать. На рис. 9.10 стрелками показано возрастание величин х и у, равнодействующая этих процессов – суммарный вектор – показывает тенденцию развития процесса. Таким образом, с течением времени в области I решение приходит в точку равновесия.

Подобным же образом анализируя возможные расположения на­чального состояния в областях II, III и IV, получим в итоге, что стабильное состояние (баланс сил) достигается независимо от на­чальных уровней вооружения стран X и Y. Отличие состоит лишь в том, что если переход к стационарному состоянию из области I со­провождается одновременным увеличением уровней вооруженности, то из области III — их одновременным снижением; для областей II и IV иная ситуация — одна из сторон наращивает свое вооружение, в то время как другая разоружается.

I II III IV

Рис. 9.10

Возможны и другие случаи. Пусть система уравнений Ричардсона имеет следующий вид:

= 5x − 3у – 11

= 4 y − 3x – 11.

Прямые, описываемые уравнениями

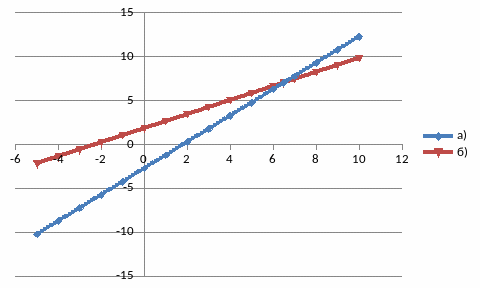
a) 5x − 3у – 11 = 0

b) 4y − 3x – 11 = 0

­

пересекаются в точке M* ( 7; 8), отмеченную на рис. 9.11.

Соответствующие четыре области в этом примере буду выглядеть так:

I – (–,–), II – ( +,–), III – (+,+), IV – (–,+),

M* I (–,–) II (+,–) III(+,+) IV (–,+)

Рис. 9.11

При начальных условиях во всех четырех областях решение будет стремиться сместиться от точки равновесия. Ситуация будет развиваться к конфликтной. Если система уравнений Ричардсона будет иметь следующий вид:

= 4 y − 3x – 11

= 5x − 3у – 11.

Здесь просто поменяли местами зависимости для и . То по-прежнему прямые описываются уравнениями:

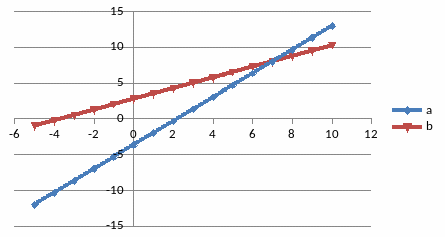
a) 4 y − 3x – 11 = 0

b) 5x − 3у – 11 = 0,

и точка пересечения прямых M* (7;8). Но области графика будут выглядеть иначе:

I – (–,–), II – (–,+), III – (+,+), IV – (+,–).

Ситуация на соответствующем графике отразится следующим образом (Рис. 9.12).

M* I (–,–) III(+,+) II (–,+) IV (+,–)

Рис. 9.12

В областях I и III система будет стремиться в сторону от точки равновесия, а в областях II и IV система будет стремиться к точке равновесия. Эта модель была построена Ричардсоном уже после Второй Мировой войны, но возможности построенной модели про­верялись на реальной ситуации, сложившейся до построения модели — гонке вооружений перед Первой мировой войной. Проведенные исследования показали, что, ­ несмо­тря на свою простоту, эта модель достаточно достоверно описывает положение дел в Европе в 1909-1913 гг. На удивление оригинальная работа Ричардсона пребывала в безвестности в течение ряда десятилетий. Модель приобрела известность уже после смерти автора. В конце 50-х годов ее обнаружила и стала всячески рекламировать группа социологов из Чикагского и Мичиганского университетов. К началу 70-х годов модель была испробована уже сотни раз на самых разных вариантах гонки вооружений. Модель показала свою способность адекватно отражать реалии конкретного события гонки вооружений.

Рис. 9.13

 Одной из важнейших характеристик модели Ричардсона является стабильность. Под стабильностью здесь понимается то, какими ускоренными или замедленными темпами происходит гонка вооружений. Стабильная гонка вооружений вернется к равновесию, а нестабильная будет удаляться от него. Такие ситуации мы разобрали на рис. 9.10 и 9.11.

На рис. 9.13. показаны два примера гонки вооружений, взятых из не такой уж давней истории: стабильной гонки вооружений между странами НАТО и ОВД и нестабильной между Ираном и Ираком. Эта схема взята из книги Дж.Б. Мангейма и Р.К. Рича «Политология: методы исследования». На обеих схемах размеры военных расходов приведены согласно данным ежегодников Международного института мирных исследований в Стокгольме (SIPRI). Как оказалось, модель Ричардсона умеет очень хорошо предсказывать войну, поскольку почти всем современным войнам предшествует нестабильная гонка вооружений. Ричардсон постулировал это в своей основополагающей работе, а впоследствии это было подтверждено другими, более детальными исследованиями.