2. Примеры стратегии вывода

Рассмотрим формализм нормальных алгоритмов Маркова, в котором правила вывода реализуются на основе операторов подста­новки.

Пусть а и b- произвольные слова. Будем говорить, что слово а входит в словоb, если существуют такие слова с иd, чтоb=cad.

Основным правилом вывода является подстановка. Оператор под­становки аbиспользуется для замены левого вхождения слова а на словоb. Для того, чтобы применить оператор аbк словуe, необ­ходимо, чтобы е содержало а. В последнем случае будем говорить, что выполнены условия применимости оператора аb. Из множества операторов, для которых выполнены условия применимости, всегда выбирается один оператор (например, первый по порядку). Отметим, что вывод считается детерминированным, если всякий раз условия при­менимости выполняются не более чем для одного правила вывода. Алгоритм завершает работу, если либо нет выполнимых операторов, либо выполняется специальный оператор конца (стоп-оператор).

Пример.

(1)a  bc

(2) c  ebcc

(3) c  d

(4) d  

(5) b  

(6) есс  d.

e- символ пробела.

Рассмотрим, как преобразуется в этой системе слово cad:

cad ebccad  eccad  dad  ad  bcd  cd  ebccd  eccd  dd  d  

Здесь внизу под стрелкой указан номер оператора.

В системах нормальных алгоритмов Маркова выводимость трак­туется в конструктивном смысле - как получение из исходного слова (образца) других слов. Это - так называемый вывод по образцу (на­шедший применение, например, в системах, использующих фреймы и семантические сети). Каноническая продукционная система Поста так­же является системой вывода по образцу.

Пусть x₁,x₂, ...,x_n- попарно различные переменные, которые име­ют области определенияD₁,D₂, ...,D_mсоответственно. Если переменная х связана некоторым значениемизD_j, , то будем вместо х, писать.

Образец это конструкция



где каждому x_i, сопоставлен терм у_i, являющийся либо самой перемен­ной х_i, (если она не связана), либо, еслиx_i=.

Например,

₁=

Пусть даны два образца ₁и₂. Будем говорить, что из₁и₂выводится образец₃, и писать это:, если выполнены следующие условия:

1. ₁и₂содержат общие переменные

2. пустьx_i- одна (любая) из общих переменных, тогдаx_iи в₁, и в₂либо связана одним и тем же значением, либо как минимум од­на из них не связана вовсе.

3. ₃образуется путем включения (без дублирования) всех перемен­ных из₁и₂. При этом если общая переменнаяx_iсвязана, скажем в₁, значениемх_i = а, а в₂свободна ( не связана), то в₃x_iбудет иметь значениеа. В этом случае говорят, что переменные в₃наследуют значения соответствующих переменных в₁,₂.

Пример вывода по образцам ₁,₂образца₃.

₁=

₂ =

из ₁, ₂выводим образец₃

₃ =

Другой важной стратегией, используемой в машинах вывода, является Байесовская стратегия вывода, которая используется в систе­мах, где детерминированность выводов является скорее исключением, чем правилом.

Байесовская стратегия вывода оперирует вероятностными знания­ми. Ее основная идея заключается в оценке апостериорной вероятности гипотезы при наличии фактов, подтверждающих или опровергающих гипотезу. Пусть

Р(Н) = - априорная вероятность гипотезы Н при отсутствии каких- либо свидетельств;

Р(Н:Е) = - апостериорная вероятность гипотезы Н при наличии свидетельства Е.

Согласно теоремы Байеса:

(1.26)

и

гдеР(Н*) оценивает новую вероятность гипотезыНс учетом свиде­тельстваЕ.

Введем отношение правдоподобия ОП(Н:Е),

(1.27)

а также формулу для вычисления шансов O(H),

(1.28)

Из (1.28) нетрудно обратным преобразованием получить

(1.29)

Теперь формула Байеса (1.8) на языке шансов принимает следую­щий вид:

O(H*) = O(H) OП(H:E), (1.30)

где O(Н*) - новая оценка шансов для гипотезы Н с учетом свидетельст­ва Е.

Формула (1.30) при наличии многих свидетельств E₁,E₂, ...,E_nпри­нимает вид:

(1.31)

Таким образом, на основании формул (1.30) и (1.31) имеется воз­можность просто пересчитывать апостериорные вероятности гипотез на основании получаемых свидетельств. Теорема Байеса является основой механизма вывода в экспертных системах PROSRECTORиHULK.

Рассмотрим пример использования стратегии Байеса. Пусть требуется провести дифференциальную диагностику между заболева­ниями D₁,D₂, ...,D_n. Для простоты, пусть имеется три заболевания и че­тыре признака, по которым должен быть составлен диагноз.

Заболевания:

D₁- тетрадаФалло,D₂- дефект межпредсердечной перегородки,D₃- незараценный артериальный проток.

Признаки:

S₁- цианоз,S₂- усиление легочного рисунка,S₃- акцент II тона во втором межреберье слева,S₄- правограмма (ЭКГ).

Допустим, известны следующие условные и безусловные вероят­ности (табл. 1.2), полученные на основе накопленной статистики о боль­ных данными заболеваниями.

Таблица 1.2

Dj	P(Dj)	P(S1/Dj)	P(S2/Dj)	P(S3/Dj)	P(S4/Dj)
D1	0,35	0,9	0	0,05	0,6
D2	0,15	0,15	0,8	0,8	0,8
D3	0,50	0,10	0,95	0,90	0,10

Пусть у пациента налицо все четыре признака: S₁,S₂,S₃,S₄. Каков диагноз заболевания? На основе теоремы Байеса можно оценить апо­стериорные вероятности заболеваний в предположении, что признакиS₁,S₂,S₃,S₄независимые. Найдем

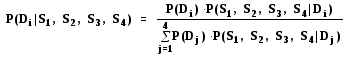(1.32)

Из условия независимости признаков имеем:

P(S₁, S₂, S₃, S₄|D_i) = P(S₁|D_i)  P(S₂|D_i)  P(S₃|D_i)  P(S₄|D_i) (1.32)