3.4.2. Стратегии перебора с отсечениями

Примером очень сильной стратегии перебора с отсечениями являет­ся метод ветвей и границ. Можно также указать( - )- процедуру Нильсона.

3.4.2.1. Метод ветвей и границ

Метод ветвей и границ разработан Литлом, Мерти, Суини и Каре­лом. Рассмотрим основные идеи этого метода. Прежде всего, этот метод связан с некоторой общей схемой допущения и оценки альтернатив. Схема построения альтернативных предположений в общем виде может быть представлена, как это показано на рис. 3.9.

Вершины на рис. 3.9 соответствуют, как и ранее, состояниям зада­чи. Из каждой вершины выходит только два альтернативных направле­ния, что, впрочем, не ограничивает общности рассмотрения. Направле­ния отмечены буквамиПс индексами. ИдентификаторR(b_i)есть неко­торая числовая оценка, приписываемая вершинеb_i.

Вообще говоря, не имеется ограничений на глубину построения де­рева, хотя ясно, что нужно стремиться к минимальной глубине. Этим, в частности, обосновывается выбор того или иного предположения П_m: сначала следует стремиться доказать предположение, достоверность которого в наибольшей степени сомнительна, или наоборот, попытаться опровергнуть предположение, достоверность которого в наибольшей степени правдоподобна, т.е. действовать по принципуreductioadabsurdum, поскольку вероятность получения противоречия здесь наи­большая, это позволяет отсечь соответствующую альтернативу у ее "ис­токов", вместо того, чтобы строить новые альтернативные предполо­жения.

Пусть ищется состояниеb^*,в которомR(b^*)минимально. Допус­тим далее, что известно некоторое текущее решениеb_xс текущим рекор­домR(b_x). Тогда ясно, что любое состояниеb_i, в котором наилучшее достижимое значениеR(b_i)  R(b_x), может быть удалено (соответствующая часть дерева поиска отмечена, как показано с помощью заштрихованной области на рис. 3.9).

Рис. 3.9

Рассмотрим задачу коммивояжера в следующей частной поста­новке. Пусть дано множествоNиз 4 городов, соединенных дорогами. Будем интерпретироватьNсетью, в которой вершины соответствуют городам, причем дугам, соединяющим вершины, приписаны весас_ij, учитывающие затраты на переход коммивояжера из городаiв городj(рис. 3.10а).

П

	1	2	3	4
1		5	6	7
2	3		4	2
3	2	1		8
4	4	4	3	

олагаемс_ij  0ис_ii = , причем необязательно, чтобыс_ij = с_ji. Будем кодировать задачу матрицей затрат С = [с_ij], показанной на рис. 3.10,б.

а) б)

Рис. 3.10

В задаче коммивояжера требуется найти цикл с минимальной сум­мой затрат образующих его дуг, который обходит каждую вершину не более одного раза, за исключением одной вершины, из которой цикл "стартует" и в которой он же "заканчивается".

Рассмотрим решение этой задачи методом ветвей и границ. Решающими оказываются следующие два обстоятельства.

А1) Решению задачи коммивояжера соответствует выбор ровно од­ного элемента в каждой строке матрицы затрат С и ровно одного эле­мента в каждом столбце этой матрицы, причем сумма выбранных эле­ментов минимальна и они образуют цикл. Последнее замечание сущест­венно. Например, элементы (1, 2), (2, 3), (3, 1), (4, 4) не образуют цикл.

А2) Если из любой строки (столбца) вычесть (добавить) одну и ту же константу D, то результирующее значение С* суммарных затрат в оптимальном цикле Ц* уменьшится (увеличится) ровно на эту величину D.

Воспользуемся свойством А2. Выпишем минимальные элементыh_jв каждом столбцеj, после чего вычтем их из элементов соответствую­щих столбцов. Затем в полученной матрице выпишем минимальные элементыh_iв строкахi. Получим приведенную матрицу на рис. 2.11, а. Вычтем из каждой строки соответствующее значениеh_i(рис. 3.11, б).

Из матрицы на рис. 3.11, б легко устанавливается, что минимально возможное значение С*(которое обозначим) вычисляется следую­щим образом

Теперь будем строить предположения для приведенной матрицы затрат на рис. 3.11, б.

Сделаем допущение, что дуга принадлежитЦ*;альтернатив­ное допущение означает, что. Если дуга, то полагаем для дугис_4,3=, а также удаляем из матрицы затрат на рис. 2.11, б строку 3 и столбец 4, что в итоге дает матрицу, показанную на рис. 2.12, а. Приведенная матрица изображена на рис.2.12, б.

Для матрицы на рис. 2.12,б находим . Таким образом, получаем, что длина оптимального цикла, содержащего дугусуть

г

де определено из матрицы на рис. 2.12, б.

	1	2	3	4	hi				1	2	3	4	hi
1		4	3	5	3			1		1	0	2	3
2	1		1	0	0			2	1		1	0	0
3	0	0		6	0			3	0	0		6	0
4	2	3	0		0			4	2	3	0		0
hj	2	1	3	2				hj	2	1	3	2

а) б)

Рис. 3.11

	1	2	3				1	2	3	hi
1		1	0			1		0	0	0
2	1		1			2	0		1	0
4	2	3				4	0	1		1
hj	1	1	0			hj	1	1	0

а) б)

Рис. 3.12

В то же время длина цикла равна 5+2+3+2=12, следовательно, делаем вывод, что дугане входит в оптимальный цикл. Полагаемс_3,4 = .

Допустим теперь, что дуга . Проведя аналогичные вы­кладки устанавливаем, что минимальная суммарная величина затрат для цикла, содержащего дугу, составляет 13 единиц. Следователь­но, это допущение также отбрасывается, т.к. оно не улучшает текущий рекорд. Полагаемс_1,4 = .

В результате в столбце 4 матрицы на рис. 3.10, б останется единст­венный допустимый элементс_2,4 = 2. Полагаем,. Это допущение позволяет удалить строку 2 и столбец 4. В результате получаем приведенную матрицу, изображенную на рис. 3.13, для кото­ройЦ*равно 12.

Допустим, что дугаТогда автоматически следует, что дуга. Удалим строку 4 и столбец 3: получим приведенную матрицу, изображенную на рис. 3.14, из которой автоматически сле­дует, что дуга. Таким образом, из исходного предположения о том, что дуга, устанавливаем следующий оптимальный цикл, не содержа­щий дуги:

с суммарными затратами, равными 2 + 3 + 2 + 5 = 12.

	1	2	3	hi									1	2	hi
1		1	0	0				1	2			3	0	1	0
3	0	1		0			1		1			4	2	3	2
4	2	3	0	0			3	0	1			hj	0	1
hj	0	1	0

Рис. 3.13 Рис. 3.14 Рис. 3.15

Проверим теперь другую альтернативу:. Из этого допу­щения получим приведенную матрицу, изображенную на рис. 3.15. Не­посредственно устанавливаем из рис.3.11, б и 2.15, что оптимальный цикл, содержащий дугу, имеет минимально возможные суммарные затраты, равные

определяется ич матрицы на рис. 3.13.

Таким образом, эта альтернатива отсекается, и мы получаем опти­мальный цикл

,

суммарной величиной затрат, равной 12. Дерево поиска, которое было построено в ходе решения задачи, изображено на рис. 3.16.

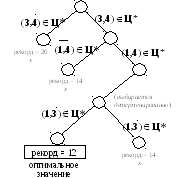
Рис. 3.16

Символом “Х” обозначены отсекаемые направления, раскрытие которых гарантированно не улучшает рекорд. Отметим, что в этой задаче был сразу использован в качестве текущего рекорда оптимальный цикл, что, впрочем не снижает общности рассуждений, однако сокращает размеры построения дерева решения.