2.5.9.1.4. Однозначность вычислений над дизъюнктивной базой

Обобщим введенные понятия на ситуацию с дизъюнктивными фактами. Пусть d_k -множество конъюнктивно связанных фактов. Тогда дизъюнк­тивным состоянием базы назовем любое конечное множество

Основные понятия совпадают с введенными выше. Определим вывод по продукции в дизъюнктивной базе.

Пусть задано: и продукцияpr = <q, r>.

Определение 7. Будем говорить, что издизъюнктивно выводимо по продукцииpr, если найдутся такие (подстановка),k(1 k  m), что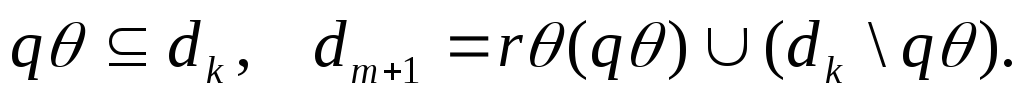

Очевидно, что любая система продукций конфлюэнтна относительно дизъюнктивного вывода, и все возможные результирующие ситуации, получаемые конъюнктивным выводом, входят в результирующую ситу­ацию в виде дизъюнктных членов.

Дизъюнктивный вывод представляет собой полный перебор альтер­нативных вариантов, основной недостаток которого — комбинаторный рост дизъюнктов. Для его реализации в работе [43] предложен метод "снизу-вверх" с использованием отношения несовместности на фактах, принадлежащих различных вариантам вывода.

Однако вывод с отношением несовместности несмотря на все сред­ства оптимизации основан на алгоритме полного перебора. Поэтому в формальной модели необходимо разработать средства для представления эвристических функций сокращения перебора и управления выводом.

2.5.9.2. Управление выводом в системах продукций

При описании предметных областей традиционно выделяют два вида знаний: логический,используемый при решении задач, иуправляющий, описывающий основные стратегии и методы решения задач. На ран­них этапах конструирования СП эти виды знаний не отделялись друг от друга, и обычная схема вывода в СП не предусматривала никаких средств управления: продукция могла применяться только в случае, ко­гда были истинны условия ее применимости. Однако во многих предмет­ных областях необходимы средства представления управля­ющей информации, поскольку решение задачи часто требует знания о планах и последовательности действий. Кроме того, при значительных объемах знаний размеры деревьев поиска решения задач оказываются очень большими, что делает обе процедуры систематического перебора (в глубину и ширину) в высшей степени непривлекательными.

Эксплицитное разделение знаний¹дает, по мнению многих авторов, два основных преимущества:

17. логические знания, если из них максимально убраны управляющие, будут ясным, корректным и лаконичным описанием предметной области;

18. управляющие знания, влияющие на эффективность системы, в ре­зультате отделения от логических проще улучшать и оптимизиро­вать.

Таким образом, выработка адекватных способов представления упра­вляющих знаний, которые не изменили бы сущности СП и сохраняли такие их важнейшие свойства, как расширяемость и способность к са­моредактированию, является одной из основных задач при разработке технологических комплексов.

Управление выводом в СП распадается на два основных типа: упра­вление продукциями и управление данными. Рассмотрим каждый из них более подробно.

2.5.9.3. Язык управления применением продукций

Описание процедур разрешения конфликта сводится обычно к заданию порядка применения продукций, называемому иногда дисциплиной при­менения. При этом порядок может быть либо детерминированным, когда на каждом шаге задается ровно одна продукция, либо недетерминиро­ванным, когда проверяются условия нескольких продукций, но их число значительно меньше общего количества правил в системе.

По способу задания можно выделить встроенный и настраиваемый порядки применения продукций. К встроенным относятся средства, ко­торые непосредственно запрограммированы в интерпретаторе системы. Примером встроенного порядка применения правил может служить схе­ма выбора правил в нормальных алгоритмах Маркова. На каждом шаге вывода проверяются условия только одного правила (на первом ша­ге — первого), если оно не применимо, то происходит переход к следую­щему. Если оно применилось, то на следующем шаге снова проверяются условия первого правила и т.д. В системе продукции можно упорядочивать по частоте использования или по самым длинным спискам условий, по приоритету и т.п. Кроме этого, в различных системах широко использовалось введение меток и тегов, специальных логических символов внутри продукции для задания последовательности выбора. Такие средства управления порядком применения продукций ак­тивно использовались в начальный период конструирования СП, когда под каждую процедуру разрешения конфликта программировался свой интерпретатор. Позднее эти средства подверглись острой критике мно­гими авторами, поскольку их введение означало отход от идеологии СП к традиционным средствам программирования. Это послужило толчком к развитию настраиваемых средств управления.

Первой попыткой в этом направлении было использование в систе­ме HEARSAY-IIразбиения правил на подсистемы таким образом, чтобы в каждый момент времени рассматривалось лишь их приемлемое чис­ло [90]. Другим средством задания порядка являются метапродукции, использованные в комплексе системMYCIN-TEIRESIAS[84]. Однако по­следовательность управляющей информации невозможно описать одни­ми метапродукциями (необходимо введение метаметапродукций и т.д.). По существу, идея введения метапродукций состоит в попытке задать всю возможную информацию в системе однородным образом.

Еще одним средством управления порядком применения правил явля­ется использование языков управления. Опишем неформально управля­ющие формулы и их использование при выводе.

Пусть Рr={< q_i r_i >}, i = 1 ... n,п  0 —множество продукций,d —текущее состояние базы данных. На языке управления порядком за­даетсяуправляющая формула,описывающая множество продукций, для которых на текущем шаге выводаtпроверяются условия применимости. Такие множества будем называть множествамиактивированныхпродукцийa_r , a_r  Рr.

Каждая продукция рr=<q,r> в задаваемом множестве может быть в одном из трех состояний:

• рr+ — условие продукциирr, активированной на шаге выводаt, должно быть истинно после проверки, т.е. найдется подстановка такая, чтоqd;

• рr-— условие продукциирr, активированной на шаге выводаt, должно быть ложно после проверки, т.е. не существует подстановкитакой, чтоqd;

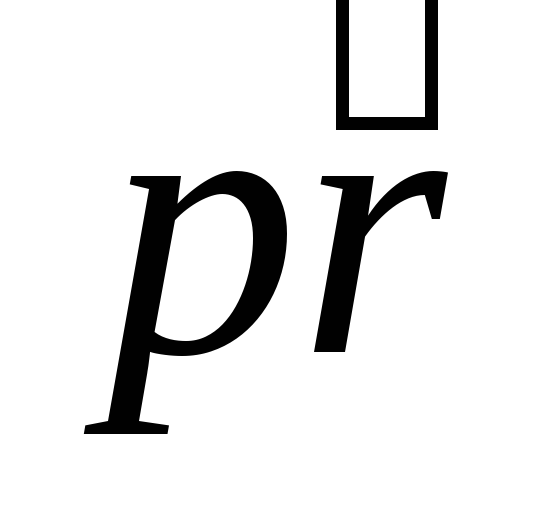• —продукция должна быть активирована, а значение ее условий (истинное или ложное) не влияет на переход к следующему шагу вывода.

Если, например, А_r=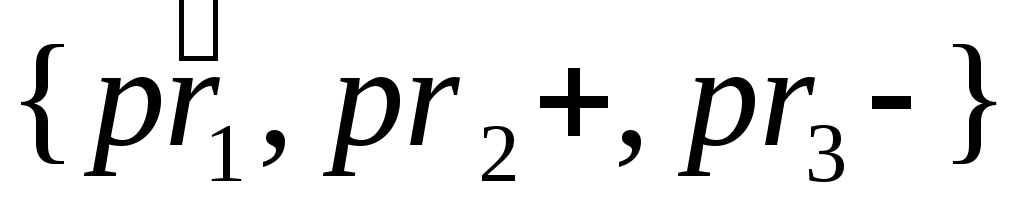, то переход кA_r+1произой­дет в том случае, если условиярr₂истинны, арr₃ложны. Истинность условийpr_iне влияет на переход кA_r+1.Требование ложности условийрr₁является одним из средств задания отрицательного контекста, если он необходим при выводе.

Язык управления представляет собой множество правильно постро­енных формул {} над состояниями продукций и бинарными операциями между ними, среди которых выделены следующие проверки условий: по­следовательная (•), одновременная (,) и альтернативная (;). Такие фор­мулы называютсяуправляющими,а множество продукций с заданной на нем управляющей формулой — системой структурированных продукций.

Опишем неформально процесс вывода в Рrс управляющей формулойна некотором шагеt. Для каждого шага выводаtпоформируется множествоА_r,которое состоит из

где

19. —множество продукций, помеченных состоянием +, т.е. про­дукций, условия которых должны быть истинны на текущем шаге вывода r;

20. —множество продукций, помеченных состоянием -, т.е. продук­ций, условия которых должны быть ложны на шаге вывода r;

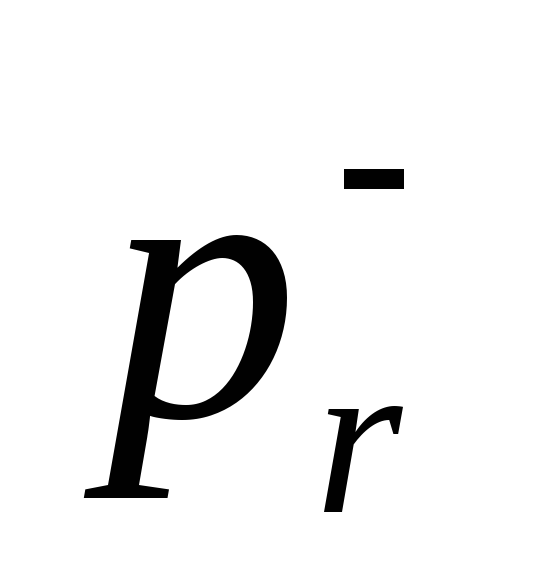21. —множество продукций, для которых не требуется однозначно­го ответа на вопрос, истинны ли их условия применимости на теку­щем шаге вывода, однако по мнению эксперта их разумно включить в число правил, у которых следует проверить условия применимо­сти, и если они истинны, то применить правила.

После проверки условий A_rраспадается на два непересекающихся подмножества:



где имножества всех активированных продукций с истинными и ложными условиями применимости соответственно.

Если выполнено условие , то применяются все продукции из множестваи происходит переход к следующему шагу вывода. Вывод заканчивается успешно, если очередноеA_rпусто. Если указанное условие не выполнено илиA_rсодержит специальный выделен­ный символ, то вывода "зависает".

Как видно из неформального описания, введение средств управления позволяет сокращать число активируемых правил. Однако это возлагает большую ответственность на эксперта, поскольку выбранная им дисци­плина применения правил может оказаться неудачной.

Рассмотрим пример использования языка управления для решения задачи определения языка, порождаемого следующей формальной грам­матикой:

Приведенная контекстно-свободная грамматика порождает язык:

Введем над этой грамматикой управляющую формулу, которая описы­вается выражением

где ()* задает итеративное применение правил p2, p3 p4.

Данное выражение может быть изображено сетью переходов на рис.1.6

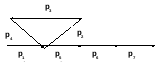
Рис. 1.6. Сеть переходов для языка управления

В результате использования управляющего языка множество слов будет представлять собой язык {aⁿbⁿcⁿ|n1}, который не является контекстно - свободным.

Как видно даже из этого небольшого примера язык управления при­менением правил позволяет значительно упрощать основные продукции.