2. Метод линейного вывода в lЛавленда, Ковальского и Кюнера

Рассмотрим пример линейного вывода. Пусть дано

Введем дополнительные определения:

1. Входная резолюция– это применение правила резолюции, в котором одна из посылок – входной дизъюнкт (входная резолюция – это частный случай линейной резолюции).

2. Входным дизъюнктомявляется каждый член исходного множестваS дизъюнктов.

3. Входной вывод– это вывод, в котором любое применение резолюции является входной резолюцией.

4. Входное опровержение– это входной вывод дизъюнктаизS.

5. Упорядоченный дизъюнкт– это последовательность различных литер. Это означает, что мы должны установить порядок всех литер в дизъюнкте. Примем соглашение, что литераL₂меньше, чем литераL₁, в дизъюнктеСв точности тогда, когдаL₂следует заL₁в последовательности, указанной в задании этого дизъюнкта. Таким образом, последняя литера всегда будет считаться наибольшей в дизъюнкте.

Уточним, что же предложили Лавленд, Ковальский и Кюнер.

Для этого рассмотрим пример. Здесь дизъюнкт p не является входным дизъюнктом. При этом легко видеть, что входное опровержение дляисходного множества S отсутствует. Поэтому неизбежно использование одного из центральных дизъюнктов в качестве бокового. Однако, тогда возникает необходимость поиска необходимого и достаточного условия, при котором боковой дизъюнкт должен быть одним из ранее порожденных центральных дизъюнктов.

Так вот, информация об отрезаемых литерах, записанная надлежащим образом, а также использование упорядоченного дизъюнкта дают возможность определить это условие. Уточним один важный момент -о записи отрезаемых литер.

Пусть С₁ и С₂ следующие упорядоченные дизъюнкты:

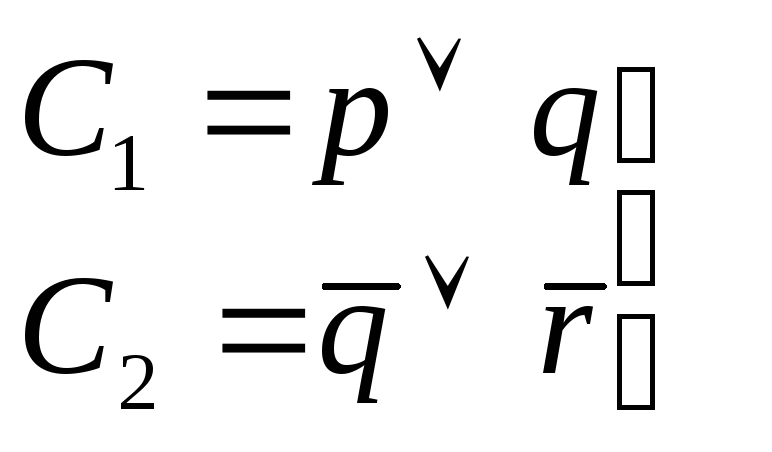
Результатом резолюции этой пары будет упорядоченный дизъюнкт – (p  r). При этом литерыqи- контрарны, примем соглашение, что результат их дизъюнкции удалять не будем, а запишем его в виде одной левой литеры, обрамленной ее в рамку.Обрамленная литера– этоотрезаемая литера, которая учитывается в дальнейших резолюциях следующим образом:

1. Обрамленную литеру должны выбрасывать только тогда, когда за ней не следует никакая необрамленная литера.

2. Если в упорядоченном дизъюнкте имеется более одного вхождение одной и той же необрамленной литеры, то всегда сохраняем самое левое вхождение, остальные совпадающие отбрасываем. Этот процесс называется отождествлением влево.

Перерисуем предыдущий пример

Здесь дизъюнктpq- редуцируемый дизъюнкт, который сразу дает пустой дизъюнкт.

Это и есть необходимо и достаточное условие использования централизованного дизъюнкта в качестве бокового. В нашем случае это дизъюнкт р.

Применяя резолюцию дизъюнктов

Все литеры в результате обрамлена, т.е. за ними не следует необрамленная литера, поэтому мы их удаляем все, в результате получаем пустой дизъюнкт, т.е линейное опровержение. 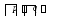Порождаемые дизъюнкты типа называютсяредуцируемыми, их появление означает, что некоторый централизованный дизъюнкт нужно использовать в качестве бокового.

П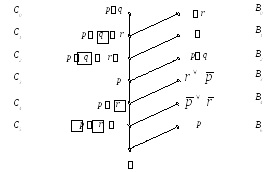ример: