3.3. Управление процессом решения задачи

Схема управления решением задачи может быть либо формализована в самой модели знаний, либо являться внешней по отношению к ней. В первом случае мы имеем дело с процедурными знаниями, во вто­ром - с декларативными.

Рассмотрим модель процедурных знаний, известную как рекурсивная сеть переходов (recursivetransitionnetwork(RTN)). Каждой дугеRTNприписан некоторый предикат (функция), истинное значение которого необходимо для разрешения перехода по данной дуге. На каждом такте функционирования сети производится оценка всех предикатов. При этом порядок просмотра предикатов не имеет значения. В результате определяется множество маршрутов, соединяющих начальное и конечное состояния, переходы вдоль всех дуг которых разрешены. Рассмот­римRTNна рис. 3. 1.

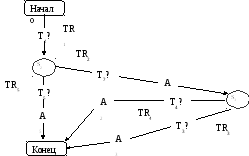
Рис. 3.1

Вершины сети соответствуют состояниям системы и образуют множество {начало, S₂, S₃, конец}. Переходы между состояниями по­меченыTR₁, TR₂, TR₃, TR₄иTR₅. ПереходуTR_i приписан предикатT_i(). Кроме того, с некоторыми из переходов связываются операто­рыA_i, которые выполняются при активации перехода. Допустим, что все предикатыT₁, ..., T₅оказались истинными. В этом случае все маршруты, связывающие вершину-начало и вершину-конец, будут разрешены и все операторыА₂, А₃, А₄, А₅будут выполнены. При этом оговаривается, что порядок выполнения операторов устанавливается согласно возрастанию их индексов. С другой стороны, если, например, ложен предикатТ₂, то будет активирован единственный маршрут(TR₁, TR₅)и возможно единственное действиеA₅. Таким образом, уп­равление выводом вRTNреализуется посредством включения уп­равляющей структуры в модель знаний.

Сеть RTNявляется примером модели знаний со встроенной детерминированной процедурой управления. В графе И-ИЛИ проце­дура управления является недетерминированной. Пустьx₁, x₂, ..., x_N- объекты некоторой предметной области, причем для каждого объектаx_iизвестна одна или несколько процедур его вычисления через другие объекты. Обозначим через_i (x_i1, x_i2, ..., x_it)процедуру вычисления объектаiчерез объектыx_i1, x_i2, ..., x_it. Каждый из объектовx_i1, x_i2, ..., x_itв свою очередь вычисляется аналогичным образом через другие объекты и т.д. Таким образом, имеется следующее функциональ­ное отношение

x_i = _i (x_i1, x_i2, ..., x_it) (3.3)

Очевидно, что если процедура_iне имеет входных данных, то объ­ектх_iпредставляет некоторое фиксированное значение, или запрашивается у пользователя. В этом случае

x_i = _i ( ) (3.4)

Соотношению (3.3) соответствует графический фраг­мент, представленный на рисунке 3.3. Двойная дужка на рис. 3.3 соответствует конъюнктивной связке вершин (связке типа "И"). Очевидно, что вполне допустимо более одной процедуры вычисления объектаx_i, причем в процедуре_jмогут участвовать иные аргументы, чем в процедуре_i; графически это соот­ветствует рис. 3.4.

Рис. 3.3 Рис. 3.4

Множество аргументов процедуры _iи_j, образуют дизъюнктивные связки (связки типа "ИЛИ"). Для вычисления объекта достаточно процедуры над одним альтернативным множеством объектов, входя­щих в одну общую конъюнктивную связку.

Формализуем задачу управления на функциональном "И - ИЛИ" графе. Пусть x₁, x₂, ..., x_N- множество объектов предметной области. Пусть даны процедуры

вычисления одних объектов через другие с числом аргументов, равным соответственно n₁, n₂, ..., n_k.

Определим состояние системы S_iкак множество переменных, значения которых известны на шагеi. ПустьS₀- начальное состояние,S_e- конечное состояние, причем конечное состояние в общем случае будет обозначаться как

S_e = {x_e1, x_e2, ..., x_ez, *}, (3.5)

где *- любое, заранее не оговариваемое множество переменных (возможно пустое), аx_e1, x_e2, ..., x_ez- множество переменных, которые обязательно должны быть определены в конечном состоянии.

Говорим, что процедура _k (x_k1, x_k2, ..., x_km)валидна (применима) в состоянииS_j, если

(x_k1, x_k2, ..., x_km)  S_j. (3.6)

Кратко тот факт обозначается как

S_j ^ . (3.7)

В интересах общности далее положим, что каждая процедура_iвы­числяет в целом более одной переменной. Ясно, что применение_i- про­цедуры в состоянииS_j, в котором она валидна, приводит в общем слу­чае к новому состояниюS_j+1, содержащему результирующие перемен­ные процедуры _i.

Задача управления заключается в построении цепочки процедурC = <_i0, _i1, ..., _iz >такой, которая обеспечивает достижение конеч­ного состоянияS_eиз начального состоянияS₀в результате последова­тельного выполнения процедур изСв указанном порядке.

Рассмотрим решение этой задачи на конкретном примере. Предва­рительно договоримся, что обозначение

_i <x_i1, x_i2, ..., x_in|x_in+1, x_i+2, ..., x_im> (3.8)

означает, чтоx_i1, x_i2, ..., x_in- это входные объекты-переменные проце­дуры, на основании которых вычисляются выходные объекты-перемен­ныеx_in+1, x_in+2, ..., x_im.

Пусть задана следующая система функций:

₁: <x₁, x₃|x₄>,

₂: <|x₁, x₂, x₅>,

₃: <x₁, x₃|x₄, x₆>,

₄: <x₂, x₅|x₄, x₆>,

₅: <x₂, x₇|x₄>,

₆: <x₁, x₃, x₄|x₆, x₈>,

₇: <x₃, x₆|x₅, x₇>,

₈: <x₅, x₆|x₉>.

Поставим в соответствие ей функциональный граф "И - ИЛИ", по­казанный на рис. 3.5. Вершины графа соответствуют объектам предмет­ной области, а дуги маркированы таким образом, что над дугой, исходящей из вершины x_iи заходящей в вершинуx_j, стоят индексы функций, в которыхx_iявляется входным аргументом, аx_jвыходным результатом. Например, дуга(x₁, x₄)помечена₁,₃, поскольку в этих функцияхx₁является входным аргументом, аx₄- выходным. ПустьS₀ = <x₁, x₃, x₅>, а S_e = <x₇, x₉, *>. Построение цепочки функцийС, вы­полняющей переход

(3.10)

осуществляется в два этапа.

Этап 1. Нормализация функционального графа.

Нормализация заключается в выполнении в произвольном порядке следующих операций, пока это возможно.

(О₁)удаление пометок всех тех функций, для которых удалены од­на или более входных вершин-переменных;

(О₂)удаление всех входных дуг, инцидентных вершинам изS₀;

(О₃)удаление вершинx_iи инцидентных им дуг таких, чтоx_i  S_e, и не имеют выходных дуг;

(О₄)удаление тех функций, которые потеряли все свои резуль­тирующие вершины-переменные. Удалению функции соответствует уда­ление идентификатора функции из числа пометок дуг. Если при этом некоторая дуга оказывается непомеченной, то эта дуга удаляется;

(О₅)если удалена дуга, помеченная, входящая в вершинуx, то по­меткаснимается со всех дуг, входящих вx, если таковые есть;

(О₆)удаление (последовательное)альтернативных вершин и ин­цидентных им дуг. Эта операция - основная. Вершинаxявляется аль­тернативной, если в результате ее удаления и инцидентных ей дуг каждая вершина, в которую заходила дуга изх, может быть вычислена некоторой цепочкойС_iиз состоянияS₀.

Рис. 3.5.

Рассмотрим рис.3.5. Так, удаляем вершину х₈согласно операцииO₃. Удаляем далее входные дуги вершиныx₅  S₀. Получаем граф на рис.3.6, а. Вершинах₂альтернативная и может быть удалена вместе с инцидентными ей дугами. Получаемый в итоге граф на рис. 3.6, б. В нем вершинах₄также альтернативная. Это последнее удаление приводит к полностью нормализованному графу на рис 3.6, в.

Рис. 3.6, а Рис. 3.6, б

Рис. 3.6, в

Этап 2. Построение уровнейL₀, L₁, ..., L_k. ВL₀войдут все верши­ны, которые не имеют входных дуг.

В уровеньL_i (i > 0)войдут все те и только те вершиных_i, которые не вошли в уровниL₀, L₁, ..., L_i-1и которые вычислимы произвольной функцией (ями)_z, выполнимой в состоянииS_i = L₀L₁...L_i-1, т.е.

S_i ^ _z. (3.11)

Так, из рис. 3.6, в устанавливаем непосредственно, что

L₀ = {x₁, x₃, x₅},

L₁ = {x₆},

L₂ = {x₇, x₉}.

Теперь в каждом уровне, исключая L, каждую вершину заменяем на ту процедуру, с помощью которой она вычислялась. Это дает следующий результат

Окончательно интересующая нас цепочка Сстроится так, чтобы любая функция_t, принадлежащая уронюL_m, стояла левее любой функции_q, принадлежащейL_n, еслиm < n; еслиm = n, то взаимный порядок расположения функций_tи_qвСроли не играет. Из этого правила, устанавливаем, например, что

C = <₃, ₇, ₈>

суть интересующая нас цепочка.

Завершим этот параграф рассмотрением моделей знаний с алго­ритмом вывода, управляемым по данным. Поскольку структура управ­ления выводом в таких моделях явно не представлена, то нужны неко­торые специальные механизмы: механизм недетерминированного выбо­ра альтернативы (альтернативной продукции), механизм возврата (бэктрекинга) и механизм унификации. Последние два механизма рас­смотрены в разделе 1.4 при описании основных понятий языка Пролог.

Механизм недетерминированного выбора альтернативы базируется на моделях, использующих так называемую эвристическую функцию оценки, введенную Н. Нильсоном. К рассмотрению этого вопроса мы приступаем в следующем параграфе.