Эффективная реализация

Условимся обозначать боковой дизъюнкт B_i сбоку от ребраC_i, тогда линейный вывод можно представить в виде дерева.Рассмотрим его на примере

Выберем в качествеC₀ =pq, тогда пригодные на первом шаге в качестве бокового – дизъюнктыи т.д.

Процесс закончен, так как порожден. Самая левая ветвь соответствуетOL– опровержению.

3.5.2.3. Метод поиска в глубину

Определение:

29. глубина дизъюнктаС₀вOL- выводе с верхним укороченным дизъюнктомС₀равна 0;

30. если глубина некоторого укороченного дизъюнкта с равна kиR– есть укороченного результата дизъюнкции С с некоторым боковым дизъюнктом, то глубина дизъюнктаRравнаk+1;

31. длина доказательства(опровержения) с верхним дизъюнктомС₀– это глубина пустого дизъюнкта.

Пусть d^*– заранее заданное пороговое число.

Описание метода:

1. Положить CLIST = (C₀)

2. Если CLIST пуст, закончим, не найдя доказательства, иначе на следующий шаг.

3. Пусть С– первый упорядоченный дизъюнкт в спискеCLIST. ВыбросимСизCLIST. Если глубинаС > d^*, то на шаг 2, иначе на шаг 4.

4. Найдем все укор. дизъюнкты в S, которые могут быть боковыми дизъюнктами дляС. Если таких боковых дизъюнктов нет, то на шаг 2. В противном случае построим результатыR₁,…,R_mдизъюнктаСс его боковыми дизъюнктами. ПустьR_i^*есть редукция дизъюнктаR_i, еслиR_iредуцируем. В противном случае положимR_i^*=R_i.

5. Если какой-либо из дизъюнктов R_q^* (1qm)пуст, то закончим, получив доказательство, иначе на следующий шаг.

6. Поместим R₁^*,…,R_m^*(в произвольном порядке) в начало спискаCLISTи перейдем к шагу 2.

Вметоде поиска в глубину узел разворачивается полностью, если он вообще выбирается для развертывания, т.е. порождаются все возможные узлы-наследники.

Смэйгл и Нильсон модифицировали этот метод.

В модифицированном методе поиска в глубину в CLISTпомещаются пары(С,В). В шестом шаге, если нет пары дляR_i*, то эту резольвенту отбрасываем.

3.5.2.4 Эвристики поиска в дереве

Использование эвристики может привести к тому, что доказательство не будет найдено, хотя оно и существует. Однако она может значительно ускорить работу модифицированного метода поиска в глубину. В области доказательства имеется много эвристик. Обсудим некоторые из них:

А. Стратегия отбрасывания.

Говорят, что упорядоченный дизъюнкт С₁поглощаетдругой упорядоченный дизъюнктС₂, если дизъюнкт, состоящий из необрамленных литер вС₁, поглощает дизъюнкт, состоящий из необрамленных литер вС₂.

Упорядоченный дизъюнкт называется тавтологией, если он содержит контрарную пару необрамленных литер.

В модифицированном методе поиска в глубину в конце шага 4 нужно проверить, является ли R_i^* (i=1,…,m)тавтологией. ЕслиR_i^*– тавтология, то отбрасываем его. Кроме того, следует отбросить R_i^*, если вCLISTимеется пара(С,В)такая, чтоR_i^*поглощается дизъюнктомС.

В. Стратегия предпочтения кратчайших дизъюнктов.

Эта стратегия вводит в модифицированный метод поиска в глубину упорядочение пар (С,В)вCLIST, чтобы лучшие пары стояли первыми. Оценивать пары рекомендуется по длине получаемого результатаLength(R). Чем короче длина, тем лучше пара(С,В).

В действительности не надо вычислять R, чтобы найти ее длину, достаточно оценки:Length (R)  Length (C) + Length (B) – 2. Смэйгл рекомендует упорядочивать пары(С,В) в спискеCLIST по возрастанию.

С. Использование эвристических оценочных функций

Определим h^*(C,B)для пары(С,В), как число применений правила резолюции в минимальном доказательстве с верхним укор. дизъюнктомСи первым боковым дизъюнктомВ.

Однако h^*(C,B) заранее неизвестна, поэтому введем оценкуh(C,B) величиныh^*(C,B). Предположим, чтоh(C,B) можно выразить в виде:h(C,B) = w₀+w₁f₁(C,B)+…+w_nf_n(C,B) (1), гдеf_i (i=1,…,n) –вещественная функция отСиВ, аw_i – вес, сопоставленный величинеf_i. (f_i называют характеристикой пары(С,В)).

Возможны следующие характеристики пар:

1. Число необрамленных литер в C.

2. Число обрамленных литер в С.

3. Число боковых дизъюнктов для С.

4. Число констант в последней литере из С.

5. Число функциональных символов в последней литере из С.

6. Число обрамленных литер в С, поглощающих последнюю литеру из В.

7. Число различных переменных в С и В.

8. length (C) + length (B) – 2

9. Число констант в С / (1+число переменных в С)

10. Число констант в С / (1+число различных переменных в С)

11. Глубина С.

12. Число необрамленных литер, входящих как в С, так и в В.

13. Число литер в В, имеющих обрамленное дополнение в С.

14. Число различных предикатных символов в С и В.

Функция h(C,B) может быть линейной или нелинейной отf₁(C,B),…,f_n(C,B), будем называть ееэвристической оценочной функцией, или просто оценочной функцией. Будем помещать пары(С,В) вCLISTпо возрастанию значенийh(C,B). Рассмотрим один из способов определения подходящих величинw₀,…,w_n.Способ определения значений множестваw.

Допустим, что мы знаем величины h^*(C₁,B₁),…,h(C_q,B_q), тогда определениеw₀,…,w_n таких, что минимально выражение(2) – оценка по наименьшим квадратам.

Определим матрицы H, F иWследующим образом:

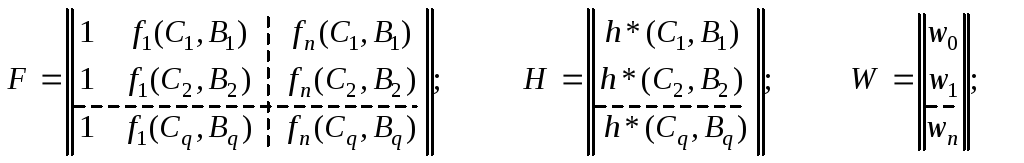
Тогда W=(F’F)^–1F’H (3), гдеF’ – транспонированная матрицаF, (F’F)^–1 – обратная матрица к(F’F).

Рассмотрим пример. Занумеруем все дизъюнкты дерева. Используем следующие характеристики.

f₁(C,B) = length (C) + length (B) – 2

f₂(C,B) = число обрамленных литер в С

f₃(C,B) = число необрамленных литер, входящих как в С, так и в В

f₄(C,B) = число литер в В, имеющих обрамленное дополнение в С

f₅(C,B) = число обрамленных литер в С, поглощающих последнюю литеру из В

Вычисляя характеристики для любой пары дерева, получим:

i	пара	f1(Ci,Bi)	f2(Ci,Bi)	f3(Ci,Bi)	f4(Ci,Bi)	f5(Ci,Bi)	h*(Ci,Bi)
	(1,2)	2	0	1	0	0	3
	(1,3)	2	0	0	0	0	4
	(4,6)	1	0	0	0	0	2
	(4,7)	1	0	0	0	0	2
	(5,8)	2	1	1	0	0	4
	(5,9)	2	1	1	1	1	3
	(10,14)	1	1	0	1	0	1
	(10,15)	1	2	0	0	0	3
	(11,16)	1	1	0	0	0	3
	(11,17)	1	1	0	1	0	1
	(12,18)	2	2	1	2	1	3
	(12,19)	2	2	0	1	1	4
	(13,20)	1	0	0	0	0	2
	(13,21)	1	0	0	0	0	2

Вычисляя по (3) W, получим:

w0=0,3	w2=0,76	w4=–1,44
w1=1,68	w3=–0,24	w5=0,6

Тогда линейная оценочная функция примет вид:

h(C,B)=0,30+1,68f₁(C,B)+0,76 f₂(C,B)–0,24 f₃(C,B)–1,44 f₄(C,B)+0,6 f₅(C,B)

Если упорядочить пары в CLIST непосредственно перед 3 шагом модифицированного метода поиска в глубину, то получим 144 ветки дерева.

Конечно, чтобы оценочная функция была хорошей,

Но нас должен волновать вопрос и о том, необходимо рассмотреть как можно больше примеров.является ли выбранное множество характеристик хорошим?

Конечно, если оценочная функция обобщается на новые примеры, то можно считать это множество хорошим, в противном случае его надо менять.