Лекции по теории и приложениям искусственных нейронных сетей

Сергей А. Терехов Лаборатотория Искусственных Нейронных Сетей НТО-2, ВНИИТФ, Снежинск

ЛЕКЦИЯ 1. Вводная.

Введение в предмет Computational Neuroscience (вычислительная нейронаука). Истоки нейронауки: достижения биологии и физиологии, психологии, дискретная математики, кибернетики, статистической физики и синергетики. Роль компьютерного моделирования. Философские основания нейронауки. Исторический обзор. Структура курса. Учебная и ознакомительная литература.

"Подмигните компьютеру - он поймет". В начале 90-х под таким заголовком в старейшей уважаемой газете Нью-Йорк Таймс появилась статья, рассказывающая о современных достижениях и направлениях в области интеллектуальных компьютерных систем. Среди магистральных путей развития данной отрасли эксперты издания выделили

• Компьютеры с высокой степенью параллелизма обработки информации, которые могут разделить ту или иную задачу на части и обрабатывать их одновременно, тем самым значительно сокращая общее время вычислений;

• Компьютеры, в которых вместо электронных сигналов для передачи информации используется оптика. Оптические сигналы уже начали использоваться для передачи данных между компьютерами;

• Компьютеры с нейронными сетями, представляющие собой машины, работающие аналогично тому, как по нашим современным представлениям, функционирует мозг.

Последнее, третье, направление, которое существенно опирается на первые два, и составляет основную тему предлагаемого курса Лекций. При этом курс сфокусирован лишь на одном из разделов направления искусственных нейронных сетей, а именно, на нейроинформатике, как науке, изучающей нейроподобные способы обработки информации при помощи компьютеров.

Разнообразие, большой об'ем и противоречивость различной диагностической информации выводят на передний план проблему поиска физических систем, способных к ее переработке. Решение этой комплексной задачи тесно связано с новыми информационными технологиями, важное место среди которых занимают методы распознавания и категоризации образов. Нейронные сети - мощный и на сегодня, пожалуй, наилучший метод для решения задач распознавания образов в ситуациях, когда в экспериментальных данных отсутствуют значительные фрагменты информации, а имеющаяся информация предельно зашумлена. Высокая степень параллельности, допускаемая при реализации нейросистем, обеспечивает обработку недоступных оператору об'емов информации за времена, меньшие или сравнимые с допустимыми временами измерений.

К рубежу 80-х годов были достигнуты значительные результаты в совсем молодой синергетике, науке о самоорганизации в неравновесных системах; систематизированы факты и проведены многочисленные новые эксперименты в нейрофизиологии, в частности, подробно изучено строение и механизм действия отдельных нейронов; сформулирован принцип работы и создана первая ЭВМ с параллельной архитектурой. Эти обстоятельства, по-видимому, стимулировали начало интенсивных исследований нейронных сетей, как моделей ассоциативной памяти.

Широкий интерес к нейронным сетям был инициирован после появления работы Хопфилда (Hopfield J.J., 1982), который показал, что задача с изинговскими нейронами может быть сведена к обобщениям ряда моделей, разработанных к тому моменту в физике неупорядоченных систем. Работа сети Хопфилда (наиболее подробно обсуждаемая в физической литературе) состоит в релаксации начального "спинового портрета" матрицы двоичных кодов к одному из стационарных состояний, определяемых правилом обучения (правилом Хебба). Таким образом, данная сеть может применяться для задач распознавания.

В 1986 году появилась работа Румельхарта, Хинтона и Вильямса (Rumelhart D.E., Hinton G.E., Williams R.J., 1986), содержавшая ответ на вопрос, долгое время сдерживавший развитие нейроинформатики - как обучаются иерархические слоистые нейронные сети, для которых "классиками" еще в 40-50 х годах была доказана универсальнось для широкого класса задач. В последующие годы предложенный Хинтоном алгоритм обратного распространения ошибок претерпел бесчисленное множество вариаций и модификаций.

Многообразие предлагаемых алгоритмов, характеризующихся различной степенью детальности проработки, возможностями их параллельной реализации, а также наличием аппаратной реализации, приводит к особой актуальности исследования по сравнительным характеристикам различных методик.

Нейронаука в современный момент переживает период перехода от юного состояния к зрелости. Развитие в области теории и приложений нейронных сетей идет в самых разных направлениях: идут поиски новых нелинейных элементов, которые могли бы реализовывать сложное коллективное поведение в ансамбле нейронов, предлагаются новые архитектуры нейронных сетей, идет поиск областей приложения нейронных сетей в системах обработки изображений, распознавания образов и речи, робототехники и др. Значительное место в данных исследованиях традиционно занимает математическое моделирование.

Необходимость написания систематического курса по теории нейронных сетей и вычислительным системам на их основе во многом определяется отсутствием отечественных учебных монографий по этой теме. Кроме того, сама эта тема пока не заняла свое место в традиционных курсах университетов и ВУЗов. И хотя промышленные эксперты американского Управления перспективных исследований DARPA ожидают начало массового распространения новой нейросетевой технологии в конце 90-х годов, уже сегодняшний уровень теоретического понимания и практического использования нейронных сетей в мировой информационной индустрии все явственнее требует профессиональных знаний в этой области.

Главной задачей предлагаемого курса является практическое введение в современные методы и системы обработки информации, об'единенные в научной литературе термином Computational Neuroscience (вычислительная нейро-наука), а также введение в перспективные подходы построения вычислительных и информационных систем новых поколений. Особенностью рассматриваемой нами темы является ее междисциплинарный характер. Свой вклад в становление нейронауки внесли биологияи физиология высшей нервной деятельности, психология восприятия, дискретная математика, статистическая физика и синергетика, и, конечно, кибернетика и, конечно, компьютерное моделирование.

Лекции содержат основную информацию о принципах организации естественных (биологических) нейронных сетей и их математических моделей - искусственных нейронных сетей, необходимую для синтеза нейросетевых алгоритмов для практических задач. Для этой цели в книгу включены две вводные темы - математическое введение (Лекция 2) и вводные биологические сведения (Лекция 3). Формальное математическое наполнение курса сведено к минимуму и опирается на базовые знания по курсам линейной алгебры и дифференциальных уравнений. Поэтому он может быть рекомендован и, в основном, предназначен для струдентов инженерных специальностей, а также математиков-прикладников и программистов.

Основные разделы курса

• Введение, сведения из биологии, физиологии высшей нервной деятельности, психологии, кибернетики, статистической физики и дискретной математики;

• Биологический нейрон и его математическая модель;

• ПЕРСЕПТРОН, линейная разделимость и теорема Розенблатта об обучении;

• Обучение нейронной сети, как задача комбинаторной оптимизации;

• Правило Хебба, модель Хопфилда и ее обобщения;

• Иерархические нейронные сети;

• Алгоритм обратного распространения ошибок;

• Модели Липпмана-Хемминга, Хехт-Нильсена, Коско;

• Способы представления информации в нейронных сетях;

• Современные нейросетевые архитектуры, КОГНИТРОН и НЕОКОГНИТРОН Фукушимы;

• Теория адаптивного резонанса;

• Алгоритмы генетического поиска для построения топологии и обучениия нейронных сетей;

• Адаптивный кластерный анализ и карта самоорганизации Кохонена;

• Конечные автоматы и нейронные сети;

• Заключение - современные день нейронауки, нейро-ЭВМ шестого поколения, нейропроцессоры, математическое обеспечение, научные и коммерческие приложения.

Литература

А. Основная

• Ф. Уоссермен. Нейрокомпьютерная техника. Москва: Мир, 1992.

• А.Н. Горбань, Д.А. Россиев. Нейронные сети на персональном компьютере. Новосибирск: Наука, 1996.

• Информатика. Справочник. Под. Ред. Д.А.Поспелова. Москва: Педагогика, 1996.

Б. Дополнительная

• Т. Кохонен. Ассоциативная память. Москва: Мир, 1980.

• Ф. Розенблатт. Принципы нейродинамики. Москва: Мир, 1965.

• Автоматы. Под. ред. К.Э. Шеннона и Дж. Маккарти. Москва: Издательство Иностранной Литературы, 1956.

• Д. Марр. Зрение. Москва: Радио и Связь, 1987.

• М. Минский, С. Пейперт. Персептроны. Москва: Мир, 1971.

• Н. Винер. Кибернетика. Москва: Советское радио, 1968.

• А.А. Веденов. Моделирование элементов мышления. Москва: Наука, 1988.

• А.Ю. Лоскутов, А.С. Михайлов. Введение в синергетику. Москва: Наука, 1990.

• С.О. Мкртчян. Нейроны и нейронные сети. Москва: Энергия, 1971.

• А.Н. Горбань. Обучение нейронных сетей. Москва: СП "Параграф", 1990.

• А.И. Галушкин. Синтез многослойных схем распознавания образов. Москва: Энергия, 1974.

• Ф.Г. Гантмахер. Теория матриц. Москва: Наука, 1988.

• Н. Грин, У. Стаут, Д. Тейлор. Биология. Под.ред. Р.Сопера. Т.1-3, Москва: Мир, 1990.

• Г. Шеперд. Нейробиология. Тт. 1-2, Москва: Мир, 1987.

• Ф. Блум, А. Лейзерсон, Л. Хофстедтер. Мозг, разум и поведение. Москва: Мир, 1988.

• Б. Банди. Методы оптимизации. М. Радио и связь, 1988

Замечание к электронному варианту 1998 г.За прошедшие 5 лет с момента написания Лекций в Российской нейроинформатике произошли значительные изменения. Разнообразные курсы по нейронным сетям начали повсеместно входить в программы высшей школы для различных технических специальностей. Появились и, немногочисленные пока, учебники, среди которых в первую очередь следует отметить книгу А.Н. Горбаня и Д.А. Россиева (1996). Увы, тираж в 500 экземпляров не позволяет рассматривать это превосходное (хотя и относительно сложное) издание в качестве базового учебника.

ЛЕКЦИЯ 2. Сведения из высшей математики.

Векторное пространство. Базис. Ортогональные проекции. Гиперсферы и гиперповерхности. Матрицы. Линейные преобразования.

Традиционно используемым для описания нейронных сетей математическим языком является аппарат векторной и матричной алгебры. Для максимального упрощения изложения, ограничивая набор общематематических сведений только этим аппаратом, хотелось бы подчеркнуть, что в современной нейронауке широко используются и другие разделы математики. Среди них - дифференциальные уравнения, применяемые для анализа нейронных сетей в непрерывном времени, а также для построения детальных моделей нейрона; Фурье-анализ для описания поведения системы при кодировании в частотной области; теория оптимизации как основа для разработки алгоритмов обучения; математическая логика и булева алгебра - для описания двоичных сетей, и другие. Изложенный в этой лекции материал носит справочный характер и не претендует на полноту. Исчерпывающие сведения по теории можно найти в книге Гантмахера, а также в стандартных курсах линейной алгебры и аналитической геометрии.

Векторные пространства.

Основным структурным элементом в описании способов обработки информации нейронной сетью является вектор- упорядоченный набор чисел, называемыхкомпонентамивектора. В дальнейшем вектора будут обозначаться латинскими буквами ( a, b, c, x ), а скаляры - числа - греческими буквами (,,,). Для обозначения матриц будут применяться заглавные латинские буквы. В зависимости от особенностей рассматриваемой задачи компоненты вектора могут быть действительными числами, целыми числами (например, для обозначения градаций яркости изображения), а также булевыми числами "ноль-один" или "минус один - один". Компоненты вектора x = ( x₁, x₂, ... x_n) можно рассматривать, как его координаты в некотором n-мерном пространстве. В случае действительных компонент это пространство обозначается, какRⁿи включает в себя набор всех возможных совокупностей из n действительных чисел. Говорят, что вектор x принадлежит пространствуRⁿ(или x изRⁿ). В дальнейшем, если нам потребуется набор векторов, мы будем нумеровать их верхними индексами, чтобы не путать с нумерацией компонент: {x¹, x², ..., x^k}.

В нашем рассмотрении мы не будем делать разницы в понятиях вектор (упорядоченная совокупность компонент) и образ (совокупностьчертилипризнаковобраза). Способы выбора совокупности признаков и формирования информационного вектора определяются конкретными приложениями.

Рис. 2.1. Примеры векторов: а) булев вектор с 25 компонентами, нумеруемыми по строкам, б) действительный вектор из пространства R⁴.

Множество векторов с действительными компонентами является частным случаем более общего понятия, называемого линейным векторным пространствомV, если для его элементов определены операции векторного сложения "+" и умножения на скаляр "^.", удовлетворяющие перечисленным ниже соотношениям (здесь x,y,z - вектора изV, а,- скаляры изR):

1. x + y = y + x, результат принадлежит V

2.  ^.( x + y ) =^.x +^.y, результат принадлежитV

3. ( +)^.x =^.x +^.x, результат принадлежитV

4. ( x + y ) + z = x + ( y + z ), результат принадлежит V

5. ( ^.)^.x =^.(^.x ), результат принадлежитV

6.  o из V:x изV=> o + x = x (существует нулевой элемент)

7. для скаляров 0 и 1, x изVимеем 0^.x = o, 1^.x = x

Свойство 1) называют свойством коомутативности, соотношения 2) и 3) - свойством дистрибутивности, а 4) - свойством ассоциативности введенных операций. Примером линейного векторного пространства является пространство Rⁿс покомпонентными операциями сложения и умножения.

Для двух элементов векторного пространства может быть определено их скалярное (внутреннее) произведение: (x,y) = x₁y₁+ x₂y₂+ ... + x_ny_n. Скалярное произведение обладает свойствами симметричности, аддитивности и линейности по каждому сомножителю:

1. ( x, y ) = ( y, x )

2. ( ^.x, y ) =^.( x, y )

3. ( x + y, z ) = ( x, z ) + ( y, z )

4. ( x, x ) >= 0, причем ( x, x ) = 0 <=> x = o

Равенство нулю скалярного произведения двух векторов означает их взаимную ортогональность, сообразно обычным геометрическим представлениям.

Два различных образа (или вектора) могут быть в той или иной мере похожи друг на друга. Для математического описания степени сходства векторное пространство может быть снабжено скалярной метрикой- расстоянием d(x,y) между всякими двумя векторами x и y. Пространства, с заданной метрикой называютметрическими. Для метрики должны выполняться условия неотрицательности, симметричности, а также неравенство треугольника:

1. d ( x, y ) >= 0, причем d ( y, x ) = 0 <=> x = y

2. d ( x, y ) = d ( y, x )

3.  y, d ( x, z ) <= d ( x, y ) + d ( y, z )

В дальнейшем изложении будут в основном использоваться две метрики - Евклидово расстояниеиметрика Хемминга. Евклидова метрика для прямоугольной системы координат определяется формулой:

Хеммингово расстояние d_Hиспользуется обычно для булевых векторов (компоненты которых равны 0 или 1), и равно числу различающихся в обоих векторах компонент.

Для векторов вводится понятие нормы||x|| - длины вектора x. Пространство в котором определена норма векторов называетсянормированным. Норма должна обладать следующими свойствами:

1. ||x|| >= 0, причем ||x|| = 0 <=> x = o

2. || ^.x || = || ||x||

3. ||x + y|| <= ||x|| + ||y||

Пространства с Евклидовой метрикой и нормой называют Евклидовым пространством. Для образов, состоящих из действительных признаков мы будем в дальнейшем иметь дело именно с Евклидовым пространством. В случае булевых векторов размерности n рассматриваемое пространство представляет собой множество вершин n-мерного гиперкуба с Хемминговой метрикой. Расстояние между двумя вершинами определяется длиной кратчайшего соединяющего их пути, измеренной вдоль ребер.

Важным для нейросетевых приложений случаем является множество векторов, компоненты которых являются действительными числами, принадлежащими отрезку [0,1]. Множество таких векторов не являетсялинейным векторным пространством, так как их сумма может иметь компоненты вне рассматриваемого отрезка. Однако для пары таких векторов сохраняются понятия скалярного произведения и Евклидового расстояния.

Вторым интересным примером, важным с практической точки зрения, является множество векторов одинаковой длины (равной, например, единице). Образно говоря, "кончики" этих векторов принадлежат гиперсфереединичного радиуса в n-мерном пространстве. Гиперсфера также не является линейным пространством (в частности, отсутствует нулевой элемент).

Для заданной совокупности признаков, определяющих пространство векторов, может быть сформирован такой минимальныйнабор векторов, в разной степени обладающих этими признаками, что на его основе, линейно комбинируя вектора из набора, можно сформировать все возможные иные вектора. Такой набор называетсябазисомпространства. Рассмотрим это важное понятие подробнее.

Вектора x¹, x², ..., x^mсчитаютсялинейно независимыми, если их произвольная линейная комбинация₁x¹+₂x²+ ... +_mx^mне обращается в ноль, если только все константы₁..._mне равны одновременно нулю. Базис может состоять из любой комбинации из n линейно независимых векторов, где n - размерность пространства.

Выберем некоторую систему линейно независимых векторов x¹, x², ..., x^m, где m < n. Все возможные линейные комбинации этих векторов сформируют линейное пространство размерности m, которое будет являтьсяподпространствомилилинейной оболочкой Lисходного n-мерного пространства. Выбранная базовая система из m векторов является, очевидно, базисом в подпространствеL. Важным частным случаем линейной оболочки является подпространство размерности на единицу меньшей, чем размерность исходного пространства (m=n-1), называемоегиперплоскостью. В случае трехмерного пространства это обычная плоскость. Гиперплоскость делит пространство на две части. Совокупность гиперплоскостей разбивает пространство на несколько множеств, каждое из которых содержит вектора с близким набором признаков, тем самым осуществляется классификация векторов.

Для двух подпространств может быть введено понятие их взаимной ортогональности. Два подпространства L₁иL₂называются взаимно ортогональными, если всякий элемент одного подпространства ортогонален каждому элементу второго подпространства.

Произвольно выбранные линейно независимые вектора необязательно являются взаимно ортогональными. Однако в ряде приложений удобно работать с ортогональными системами. Для этого исходные вектора требуется ортогонализовать. Классический процесс ортогонализации Грама-Шмидта состоит в следующем: по системе линейно независимых ненулевых векторов x¹, x², ..., x^mрекуррентно строится система ортогональных векторов h¹, h², ..., h^m. В качестве первого вектора h¹выбирается исходный вектор x¹. Каждый следующий (i-ый) вектор делается ортогональным всем предыдущим, для чего из него вычитются его проекции на все предыдущие вектора:

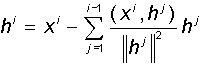
При этом, если какой-либо из получившихся векторов hⁱоказывается равным нулю, он отбрасывается. Можно показать, что, по построению, полученная система векторов оказывается ортогональной, т.е. каждый вектор содержит только уникальные для него признаки.

Далее будут представлены теоретические аспекты линейных преобразований на векторами.

Матрицы и линейные преобразования векторов.

Равно тому, как был рассмотрен вектор - объект, определяемый одним индексом (номером компоненты или признака), может быть введен и объект с двумя индексами, матрица. Эти два индекса определяют компоненты матрицы A_ij, располагаемые по строкам и столбцам, причем первый индекс i определяет номер строки, а второй j - номер столбца. Интересно отметить, что изображение на рисунке 2.1.а) может трактоваться и как вектор с 25 компонентами, и как матрица с пятью строками и пятью столбцами.

Суммой двух матриц A и B одинаковой размерности (n x m) является матрица С той же размерности с компонентами, равными сумме соответствующих компонент исходных матриц: C_ij= A_ij+ B_ij. Матрицу можно умножить на скаляр, при этом в результате получается матрица той же размерности, каждая компонента которой умножена на этот скаляр. Произведением двух матриц A (n x l) и B (l x m) также является матрица C (n x m), компоненты которой даются соотношением:

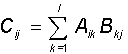
Заметим, что размерности перемножаемых матриц должны быть согласованными - число столбцов первой матрицы должно равняться числу строк второй.

В важном частном случае, когда вторая матрица является вектором (т.е. матрицей с одной из размерностей, равной единице (m=1)), представленное правило определяет способ умножения матрицы на вектор:

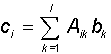
В результате умножения получается также вектор с, причем для квадратной матрицы A (l x l) его размерность равна размерности вектора-сомножителя b. При произвольном выборе квадратной матрицы A можно построить произвольное линейное преобразованиеy=T(x) одного вектора (x) в другой (y) той же размерности: y=Ax. Более точно, для того, чтобы преобразование T одного вектора в другой являлось линейным, необходимо и достаточно, чтобы для двух векторов x¹и x²и чиселивыполнялось равенство: T(x¹+x²) =T(x¹) +T(x²). Можно показать, что всякому линейному преобразованию векторов соотвествует умножение исходного вектора на некоторую матрицу.

Если в приведенной выше формуле для умножения матрицы A на вектор x компоненты этого вектора неизвестны, в то время, как A и результирующий вектор b известны, то о выражении A x = b говорят, как о системе линейных алгебраических уравненийотносительно компонент вектора x. Система имеет единственное решение, если вектора, определяемые строками квадратной матрицы A, являются линейно независимыми.

Часто используемыми частными случаями матриц являются диагональные матрицы, у которых все элементы вне главной диагонали равны нулю. Диагональную матрицу, все элементы главной диагонали которой равны единице, называютединичной матрицейI. Линейное преобразование, определяемое единичной матрицей, является тождественным: Ix=x для всякого вектора x.

Для матриц определена, кроме операций умножения и сложения, также операция транспонирования. Транспонированная матрица A^Tполучается из исходной матрицы A заменой строк на столбцы: (A_ij)^T= A_ji. Матрицы, которые не изменяются при транспонировании, называютсимметричными матрицами. Для компонент симметричной матрицы S имеет место соотношение S_ij= S_ji. Всякая диагональная матрица, очевидно, является симметричной.

Пространство квадратных матриц одинаковой размерности с введенными операциями сложения и поэлементного умножения на скаляр, является линейным пространством. Для него также можно ввести метрику и норму. Нулевым элементом служит матрица, все элементы которой равны нулю.

В заключении приведем некоторые тождества для операций над матрицами. Для всяких A,B и C и единичной матрицы I имеет место:

1. IA = AI = A

2. (AB)C = A(BC)

3. A(B+C) = AB + AC

4. (A^T)^T= A

5. (A+B)^T= A^T+ B^T

6. (AB)^T= B^TA^T

Доказательство этих соотношений может служить полезным упражнением.

Лекция 3. Биологический нейрон и его кибернетическая модель.

Нейробиология. Биологический нейрон, его строение и функции. Об'единение нейронов в сети. Биологическая изменчивость и обучаемость нейронных сетей. Кибернетическая модель нейрона - формальный нейрон МакКаллока и Питса. Обучение нейрона задаче детектирования границы яркости.

Эта лекция посвящена биологическим основаниям науки о вычислительных нейронных сетях. Также, как и в предыдущей лекции, изложение будет носить справочный характер, и предназначено для читателя, не имеющего специальных знаний по биологии. Более глубокие профессиональные сведения можно найти в относительно недавно переведенной книге Н.Грина, У. Стаута и Д.Тейлора, а также в монографии Г.Шеперда. Для ознакомительного чтения можно порекомендовать книгу Ф.Блума, А.Лейзерсона и Л.Хофстедтера.

На протяжении книги нашей основной целью будет исследование методов и кибернетических систем, имитирующих функции мозга при решениии информационных задач. Такой путь разработки искусственных вычислительных систем во многом представляется естественным - высшие биологические организмы, и особенно человек, легко справляются с такими, крайне сложными при математическом рассмотрении проблемами, как, например, распознавание образов (зрительных, слуховых, сенсорных и других), память и устойчивое управление движением тела. Биологический фундамент при изучении этих функций является крайне важным, природное многобразие дает исключительно богатый исходный материал для направленного создания искусственных моделей.

В завершении лекции будет представлена классическая кибернетическая модель нейрона - так называемый формальный нейрон Маккалока и Питтса. Некоторые свойства формального нейрона будут изучены на задаче детектирования границы перехода "черное-белое" в простом изображении.

Метод нейробиологии.

К предмету нейробилологии относится изучение нервной системы и ее главного органа - мозга. Принципиальным вопросом для этой науки является выяснение соотношения между строениемнервной системы и еефункцией. При этом рассмотрение проводится на на нескольких уровнях: молекулярном, клеточном, на уровне отдельного органа, организма в целом, и далее на уровне социальной группы. Таким образом, классический нейробилогический подход состоит в последовательном продвижении от элементарных форм в направлении их усложнения.

Для наших практических целей отправной точкой будет клеточный уровень. По современным представлениям, именно на нем совокупность элементарных молекулярных химико-биологических процессов, протекающих в отдельной клетке, формирует ее как элементарных процессор, способный к простейшей переработке информации.

Биологический нейрон.

Элементом клеточной структуры мозга является нервная клетка - нейрон. Нейрон в своем строении имеет много общих черт с другими клетками биоткани: тело нейрона окружено плазматической мембраной, внутри которой находится цитоплазма, ядро и другие составляющие клетки. Однако нервная клетка существенно отличается от иных по своемуфункциональному назначению. Нейрон выполняет прием, элементарное преобразование и дальнейшую передачу информации другим нейронам. Информация переносится в виде импульсов нервной активности, имеющих электрохимическую природу.

Нейроны крайне разнообразны по форме, которая зависит от их местонахождения в нервной системе и особенностей фунционирования. На Рис. 3.1. приведена схема строения "типичного" нейрона. Тело клетки содержит множество ветвящихся отростков двух типов. Отростки первого типа, называемые дендритамиза их сходство с кроной раскидистого дерева, служат в качестве входных каналов для нервных импульсов от других нейронов. Эти импульсы поступают всомуилителоклетки размером от 3 до 100 микрон, вызывая ее специфическое возбуждение, которое затем распространяется по выводному отростку второго типа -аксону. Длина аксонов обычно заметно превосходит размеры дентритов, в отдельных случаях достигая десятков сантиметров и даже метров. Гигантский аксон кальмара имеет толщину около миллиметра, и именно наблюдение за ним послужило выяснению механизма передачи нервных импульсов между нейронами.

Тело нейрона, заполненное проводящим ионным раствором, окружено мембраной толщиной около 75 ангстрем, обладающей низкой проводимостью. Между внутреннней поверхностью мембраны аксона и внешней средой поддерживается разность электрических потенциалов. Это осуществляется при помощи молекулярного механизма ионных насосов, создающих различную концентрацию положительных ионов K⁺и Na⁺внутри и вне клетки. Проницаемость мембраны нейрона селективна для этих ионов. Внутри аксона клетки, находящейся в состоянии покоя, активный транспорт ионов стремится поддерживать концентрацию ионов калия более высокой, чем ионов натрия, тогда как в жидкости, окружающей аксон, выше оказывается концентрация ионов Na⁺. Пассивная диффузия более подвижных ионов калия приводит к их интенсивному выходу из клетки, что обуславливает ее общий отрицательный относительно внешней средыпотенциал покоя, составляющий около -65 милливольт.

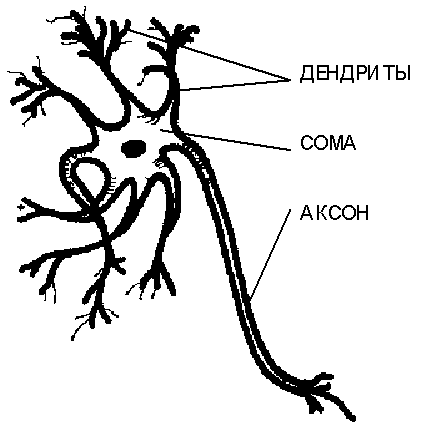
Рис. 3.1.Общая схема строения биологического нейрона.

Под воздействием стимулирующих сигналов от других нейронов мембрана аксона динамически изменяет свою проводимость. Это происходит, когда суммарный внутренний потенциал превышает пороговое значение масштаба -50 мв. Мембрана на короткое время, сотавляющее около 2 миллисекунд, изменяет свою полярность (деполяризуется) и достигает потенциала действияоколо +40 мв. На микроуровне это объясняется кратковременным повышением проницаемости мембраны для ионов Na⁺и активным поступлением их в аксон. В дальнейшем, по мере выхода ионов калия, положительный заряд с внутренней стороны мембраны меняется на отрицательный, и наступает так называемыйпериод рефрактерности, длящийся около 200 мс. В течении этого времени нейрон является полностью пассивным, практически неизменно сохраняя потенциал внутри аксона на уровне около -70 мв.

Импульс деполяризации клеточной мембраны, называемый спайком, распространяется вдоль аксона практически без затухания, поддерживаясь локальными ионными градиентами. Скорость перемещения спайка является относительно невысокой и составляет от 100 до 1000 сантиметров в секунду.

Возбуждение нейрона в виде спайка передается другим нейронам, которые таким образом объеденены в проводящую нервные импульсы сеть. Участки мембраны на аксоне, где размещаются области контакта аксона данного нейрона с дендритами другими нейронов, называются синапсами. В области синапса, имеющего сложное строение, происходит обмен информацией о возбуждении между нейронами. Механизмы синаптической передачи достаточно сложны и разнообразны. Они могут иметь химическую и электрическую природу. В химическом синапсе в передаче импульсов участвуют специфические химические вещества -нейромедиаторы, вызывающие изменения проницаемости локального участка мембраны. В зависимости от типа вырабатываемого медиатора синапс может обладать возбуждающим (эффективно проводящим возбуждение) или тормозящим действием. Обычно на всех отростках одного нейрона вырабатывается один и тот же медиатор, и поэтому нейрон в целом функционально является тормозящим или возбуждающим. Это важное наблюдение о наличии нейронов различных типов в последующих главах будет существенно использоваться при проектировании искуственных систем.