
- •Лекция 3. Биологический нейрон и его кибернетическая модель.
- •Метод нейробиологии.
- •Биологический нейрон.
- •Нейронные сети.
- •Биологическая изменчивость и обучение нейронных сетей.
- •Формальный нейрон.
- •Обучение нейрона детектированию границы "черное-белое"
- •Лекция 4. Персептрон Розенблатта.
- •Персептрон Розенблатта.
- •Теорема об обучении персептрона.
- •Линейная разделимость и персептронная представляемость
- •Лекция 5. Свойства процессов обучения в нейронных сетях.
- •Задача обучения нейронной сети на примерах.
- •Классификация и категоризация.
- •Обучение нейронной сети с учителем, как задача многофакторной оптимизации. Понятие о задаче оптимизации.
- •Постановка задачи оптимизации при обучении нейронной сети
- •Лекция 6. Многослойный персептрон.
- •Необходимость иерархической организации нейросетевых архитектур.
- •Многослойный персептрон.
- •Обучение методом обратного распространения ошибок.
- •Лекция 7. Другие иерархические архитектуры.
- •Звезды Гроссберга
- •Принцип Winner Take All (wta) - Победитель Забирает Все - в модели Липпмана-Хемминга.
- •Карта самоорганизации Кохонена.
- •Нейронная сеть встречного распространения.
- •Лекция 8. Модель Хопфилда.
- •Сети с обратными связями
- •Нейродинамика в модели Хопфилда
- •Правило обучения Хебба
- •Ассоциативность памяти и задача распознавания образов
- •Лекция 9. Обобщения и применения модели Хопфилда.
- •Модификации правила Хебба.
- •Матрица Хебба с ортогонализацией образов.
- •Отказ от симметрии синапсов.
- •Алгоритмы разобучения (забывания).
- •Двунаправленная ассоциативная память.
- •Детерминированная и вероятностная нейродинамика.
- •Применения сети Хопфилда к задачам комбинаторной оптимизации.
- •Лекция 10. Неокогнитрон Фукушимы.
- •Когнитрон: самоорганизующаяся многослойная нейросеть.
- •Неокогнитрон и инвариантное распознавание образов.
- •Лекция 11. Теория адаптивного резонанса.
- •Дилемма стабильности-пластичности восприятия.
- •Принцип адаптивного резонанса.
- •Нейронная сеть aрt-1.
- •Начальное состояние сети.
- •Фаза сравнения.
- •Фаза поиска.
- •Обучение сети арт.
- •Теоремы арт.
- •Дальнейшее развитие арт: архитектуры арт-2 и арт-3. Нерешенные проблемы и недостатки арт-1.
- •Сети арт-2 и арт-3.
- •Лекция 12. Черты современных архитектур.
- •Черты современных архитектур.
- •Сегодняшний день нейронауки.
- •Программное и аппаратное обеспечение. Нейро-эвм.
Лекция 9. Обобщения и применения модели Хопфилда.
Вероятностные обобщения модели Хопфилда и статистическая машина Больцмана. Двунаправленная ассоциативная память Коско. Представление информации в сети Хопфилда, решающей задачу комбинаторной оптимизации. Нейровычисления и нейроматематика. Принципы организации вычислительных процессов в нейроЭВМ.
Модификации правила Хебба.
Ограничения емкости синаптической памяти, а также проблема ложной памяти классической нейронной сети в модели Хопфилда, обученной по правилу Хебба, привели к появлению целого ряда исследований, целью которых было снятие этих ограничений. При этом главный упор делался на модификацию правил обучения.
Матрица Хебба с ортогонализацией образов.
На предыдущейлекции было установлено, что ортогональность образов обучающей выборки является весьма благоприятным обстоятельством, так как в этом случае можно показать их устойчивое сохранение в памяти. В случае точной ортогональности достигается максимальная емкость памяти, равная N - максимально возможному числу ортогональных образов из N компонент.
На этом свойстве ортогональных образов и основан один из наиболее часто используемых способов улучшения правила Хебба: перед запоминанием в нейронной сети исходные образы следует ортогонализовать. процедура ортогонализации приводит к новому виду матрицы памяти:
![]()
где B-1- матрица, обратная к матрице B:
![]()
Такая форма матрицы памяти обеспечивает воспроизведение любого набора из p<N образов. Однако, существенным недостатком этого метода является его нелокальность: обучение связи между двумя нейронами требует знания состояний всех других нейронов. Кроме того, прежде чем начать обучение, необходимо наперед знатьвсеобучающие образы. Добавление нового образа требует полного переобучения сети. Поэтому данный подход весьма далек от исходных биологических оснований сети Хопфилда-Хебба, хотя на практике приводит к заметным улучшениям ее функционирования.
Отказ от симметрии синапсов.
Другим подходом для улучшения правила Хебба является отказ от симметрии синаптических соединений. Матрица памяти может выбираться в следующей форме:
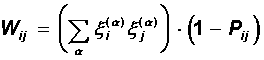
Элементы матрицы Pijиз множества {0,1} управляют наличием или отсутсвием связи от нейрона i к нейрону j.
Увеличение емкости памяти в такой модели в принципе может быть достигнуто за счет появления новых степеней свободы, связанных с матрицей P. В общем случае, однако, трудно предложить алгоритм выбора этой матрицы. Следует также отметить, что динамическая система с несимметричной матрицей не обязана быть устойчивой
Алгоритмы разобучения (забывания).
Возможность забывания ненужной, лишней информации является одним из замечательных свойств биологической памяти. Идея приложения этого свойства к искусственной нейросети Хопфилда “удивительно” проста: при запоминании образов обучающей выборки вместе с ними запоминаются и ложные образы. Их-то и следует “забыть”.
Соотвествующие алгоритмы получили название алгоритмов разобучения. Суть их сводится к следующему.
На первой фазе происходит обучение сети по стандартному правилу Хебба. Память наполняется истинными образами и множеством ложной информации. На следующей фазе (фазе разобучения) сети пред’является некоторый (случайный) образ (0). Сеть эволюционирует от состояния(0)к некоторому состоянию(f), которое при большом об’еме обучающей выборки чаще всего оказывается ложным. Теперь матрица связей может быть поправлена, с целью уменьшить глубину минимума энергии, отвечающего этому ложному состоянию:
![]()
В качестве степени забывания выбирается некоторое малое число, что гарантирует незначительное ухудшение полезной памяти, если состояние(f)не окажется ложным. После нескольких “сеансов забывания” свойства сети улучшаются (J.J.Hopfield et al, 1983).
Данная процедура далека от формального теоретического обоснования, однако на практике приводит к более регулярной энергетической поверхности нейронной сети и к увеличению об’ема бассейнов притяжения полезных образов.
