2.5.9.1.2. Операции преобразования ситуации

Определим основные преобразования ситуации, к которым относятся ис­ключение и добавление фактов. Для фиксированного d'D:

1. Операция исключения: elim[d'] : D D

elim[d'](d) = d\ d'

2. Операция добавления: аdd[d'] : D D

add[d'](d)=d  d'

Определим множество программ Rпреобразования ситуации следу­ющим образом. Во-первых, будем считать элементамиRпрограммыadd[d'], elim[d']при любыхd'D,во-вторых, если две программыr₁,r₂R,то программа (r₁; r₂) определенная равенством (r₁; r₂)(d) =r₂(r₁(d)), d D, также элементR.

Для любого r  Dвведем множествоin(r)переменных, добавляе­мых программойr,и множествоout(r)переменных, исключаемыхr, по следующим правилам:d'  D

• out(add[d']) = , in(add [d']) = var(d');

• out(elim[d']) = var(d'), iп(еliт[d']) = ;

• out (r1; r2) = out(r1)  оиt(r2), in(r1; r2) = in (r1 ; r2 )  in(r2).

Определение 3.Программуr⁺, содержащую только операции типаadd[d'](d'  D),назовемпозитивной.Заметим, чтоout(r⁺)=и, еслиd₂ = r⁺(d₁), то d₂  d₁.

Через r, где=[t₁ /x₁, ...,t_m /x_m} — произвольная подстанов­ка, обозначим программуr, во всех операциях которой аргументы-переменныеx_iзаменены на сопоставленные им втермыt_i, i=1...m. Переменные программы, которым не сопоставлены в подстановкени­какие термы, заменяются на новые, еще неиспользованные переменные из множестваX_s , sS.

Определение 4.Продукцией назовем пару <q, r>, в которойq —си­туация, называемая условием применимости продукции,r— программа,r R, называемая действием, причемqиrсвязаны соотношением

var(q)  out(r).

С

d1

pr 

d2

истемой продукций назовем конечное множество парРr={<q, r >}. Будем говорить, чтоd₂ непосредственно выводимоизd₁при помощи продукцииpr= <q,r>, , если найдется такая подстановка, чтоd₁q, а

d₂=r(q) (d₁\q).

Е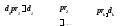сли найдется последовательность продукцийрr₁,рr₂, ...,pr_k, pr_i  Pr,i =1...k, k0, и состояний базыd₀, d₁, …,d_kтаких, что

d0

 

d1

d0

pr1,…, prk 

d1

то говорим, что d_kвыводимо изd₀,и пишем или, apr₁,рr₂, ...,pr_kназовем последовательностью применимых кd₀про­дукций.

Если иpr(=>d' = d_k), тоd_kназовем результирую­щей ситуациейd₀.

Рассмотрим вывод по продукции на примере задачи планирования химического синтеза. Предположим, что можно провести следующие хи­мические реакции:

MgO + Н₂  Mg + Н₂O ,

СиО + Н₂  Си + H₂O,

Zn + H₂S0₄  ZnS0₄ + Н₂.

Опишем предметную область посредством многосортной алге­бры с множествами носителями:

окись = {MgO, CuO},

металл = {Mg, Cu, Zn},

газ={Н₂, 0},

соль = {ZnSO₄},

кислота = {H₂S0₄},

вода= {Н₂О},

вещества = окиcь  металл газ  соль кислотa вода

и отображениями

основание:окись —> металл (например, основание (MgO) = Mg);

формула: вещества —> вещества (тождественное пре­образование, сопоставляющее веществу его химическую фор­мулу).

Тогда химические реакции можно переписать в виде следующих про­дукций (в некотором условном синтаксисе):

1) pr₁ =< q₁, r₁ >,

где q₁ = (mun, х, окись)  (основание, х, у)  (тип, у, металл)  (формула, z, Н₂)  (тип, z, газ);

r_i = add[(mun, z', вода)  (формула, z', Н₂О)  (mun,z", металл)  (формула, z",y)];

elim[(тип, x, окись)  (формула, z, H₂)  (тип, z, газ)]

2) рr₂ =< q₂, r₂ >,

где q₂ = (тип, x, металл)  (формула, х, Zn)  (формула, z, H₂SО₄)  (тип, z, кислота),

r₂ = аdd[(тип, z', газ)  (формула, z', H₂)  (тип, z", соль)  (формула, z", ZnSО₄)];

elim [(тип, x, металл)  (формула, х, Zn)  {тип, z, кислота)  (формула, z, H₂SО₄)].

Первой продукции соответствуют первые две реакции, вторая — опи­сывает третью реакцию.

Пусть имеется информация о наличии веществ {MgO, CuO, Zn, H₂SО₄}, что задается следующей исходной ситуацией:

d₀=(mun,e₁, окись)(основание,e₁,Mg)(тип, е₂, окись)(основание, е₂, Сu)(формула,e₁,MgO)(формула, е₂,CuO)(тип, е₃, металл}(формула, е₃,Zn)(тип, е₄, кислота)(формула,e₄,H₂SО₄).

Для наглядности в дальнейшем не будем выписывать факты ситуа­ции, а ограничимся лишь перечислением химических элементов, инфор­мация о которых задается ситуацией.

Ставится задача: какие вещества могут быть получены (результиру­ющая ситуация) из заданных по продукциям pr₁ — pr₂.

Рассмотрим процесс вывода. На первом шаге применима продукция рr₂, которая приводит к ситуации, описывающей наличие следующих веществ:{MgO, CuO, H₂, ZnS0₄}.

На втором шаге применима лишь продукция рr1, однако для нее су­ществуют две подстановки

₁ = {Mg/y,e₁/x}, ₂ = {Сu/у, е₂/х},

что дает в первом случае ситуацию, описывающую наличие веществ {Mg, H₂0, CuO, ZnS0₄}, а во втором —{MgO, Н₂0, Си, ZnS0₄}.

Из примера видно, что результирующая ситуация зависит в общем случае от выбора подстановки и порядка применения продукций, т.е. неоднозначна. Для СП, результат конъюнктивного вывода в которых од­нозначен, разработаны эффективные методы поиска решений (каким, на­пример, является использование смешанных вычислений [91] в реляционной модели [24]). Поэтому в этой модели СП актуальна задача выделения подклассов, в которых результирующая ситуация однозначна.