2.3.5. Булевы классификации

Другим видом классификационной схемы является ситуация, когда таксоны образуют структуру булевой алгебры. В этом случае на выделенной системе классов K_iзадаются теоретико-множественные операции объединения (), пересечения () и разности ( / ).Тогда исходная система классов превращается в булеву алгебру

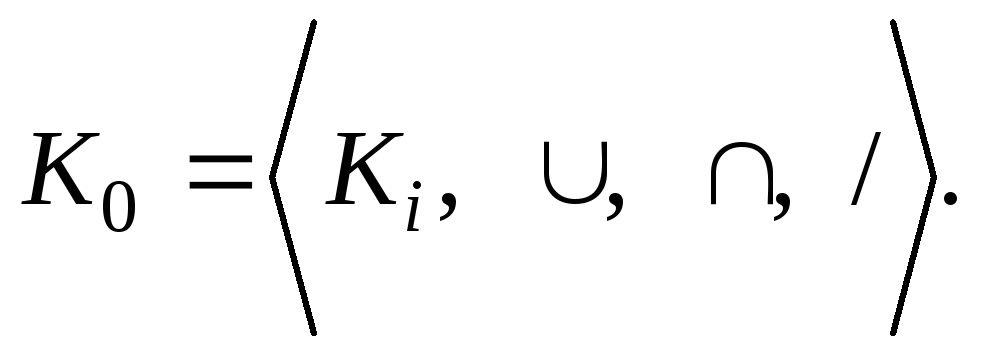
Данный тип классификационной схемы возникает, например, в случае использования дескрипторов для классификации текстов документов. В качестве примера рассмотрим множество терминов, состоящее из четырех дескрипторов: d₁,d₂,d₃,d₄. Тогда структура таксонов может состоять (рис. 4)из одного таксона Т₀, включающего все наличные тексты; четырех таксонов первого уровня Т₁¹, Т₂¹, Т₃¹, Т₄¹, включающих тексты, содержащие по одному дескрипторуd₁, d₂,d₃или d₄;шести таксонов второго уровняT₁², Т₂², Т₃², Т₄²,T₅²,Т₆², включающих тексты, содержащие по одной из пар дескрипторов (d₁,d₂), (d₁,d₃), (d₁, d₄),(d₂,d₃), (d₂, d₄),(d₃, d₄);четырех таксонов третьего уровня T₁³,Т₂³, Т₃³, Т₄³, включающих тексты, содержащие тройки дескрипторов (d₁,d₂,d₃), (d₁,d₂, d₄),(d₁,d₃,d₄), (d₂,d₃,d₄), и одного таксона четвертого уровня, включающего тексты, содержащие все четыре дескриптора (d₁,d₂,d₃,d₄).

Рис. 4. Булева классификационная структура таксонов документов

Архетипами соответствующих классов документов будут выступать множества значений дескрипторов:

arhK₁¹ = {d₁}, arhK₂¹ = {d₂}, arhK₃¹ = {d₃}, аrhK₄¹ = {d₄};

arhK₁² = {d₁, d₂}, arhK₂² = {d₁, d₃}, arhK₃² = {d₁, d₄},

arhK₄² = {d₂, d₃}, arhK₅² = {d₂, d₄}, arhK₆² = {d₃, d⁴};

arhK₁³ = {d₁, d₂, d₃}, arhK₂³ = {d₁, d₂, d₄}, arhK₃³ = {d₁, d₃, d₄}, arhK₄³ = {d₂, d₃, d₄};

arhK₁⁴ = {d₁, d₂, d₃, d₄}.

Если изучать данную классификационную структуру с точки зрения внутреннего строения ее архетипов, т.е. исходя из наличия в тексте совокупности тех или иных дескрипторов, то получим антиизоморфную картину (рис. 5).

Сопоставление таксономической структуры текстов и их внутреннего строения на основе входящих в них дескрипторов показывает, что объединению таксонов текстов соответствует пересечение множеств дескрипторов, входящих в соответствующие архетипы, а пересечению таксонов текстов –объединение множеств дескрипторов архетипов.

Структура таксонов по включению антиизоморфна структуре всех подмножеств множества дескрипторов {d₁, d₂,d₃, d₄},т.е. булевой решетке. Действительно, включение таксона Т_iT_jозначает, что таксон Т_i определяется какими-то дополнительными дескрипторами, т.е. если таксону Т_iсопоставить архетипarhК_i, а таксону T_j -архетипarhK_j, то будет выполняться соотношение arhК_iarhK_j.

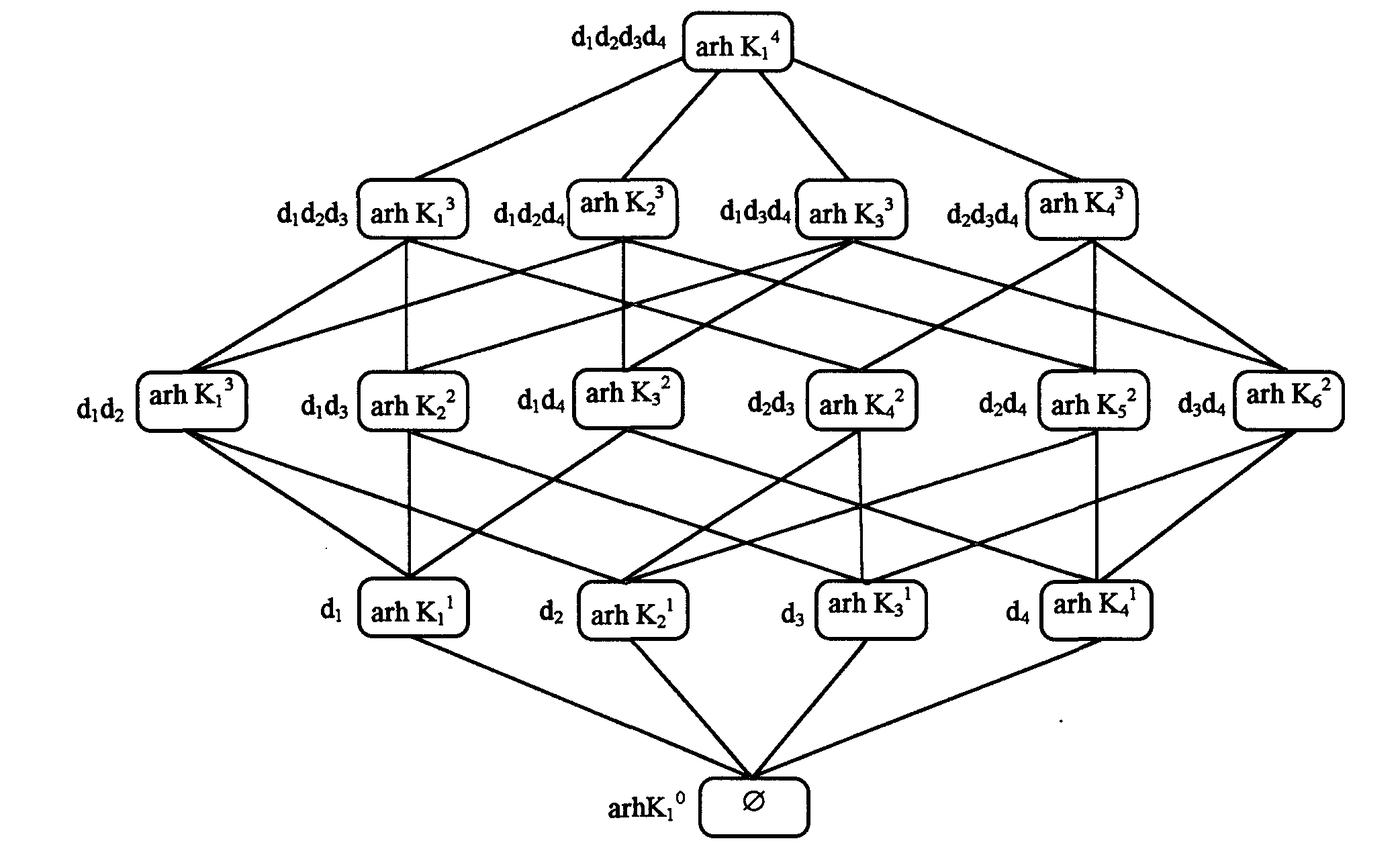
Рис. 5.Антиизоморфная структура архетипов поисковых образов документов

2.3.6. Комбинативные классификации

Комбинативные (фасетные) классификации возникают как результат классификации понятий по совокупности имен и значений их признаков.

Фасеты такой классификации определяются булевыми операциями над именами признаков и образуют булеву алгебру. Очевидно, что классификацию текстов на основании содержащихся в них дескрипторов с этой точки зрения можно рассматривать как однофасетную, так как мы имеем только один признак ДЕСКРИПТОР для всех терминов, используемых при классификации текстов. Но в комбинативных классификациях, как правило, полагают, что классификационные признаки сущностей не являются множественными.

Для выделения таксонов каждый фасет в свою очередь подвергается дополнительному делению на основе использования значений признаков. Так, если имеются признаки А, В, С, то в комбинативной классификации можно выделить три фасета первого уровня –F^A,F^B,F^C; три фасета второго уровня –F^AB,F^AC,F^BCи один фасет третьего уровняF^ABC.Таксоны первого уровня Т₁^A, T₂^A,…,T_n^A,T₁^B,...,Т_m^B, Т₁^C,...образуются путем деления каждой из фасетF^A,F^B,F^Cна основе значений признаков. Таксоны второго уровня могут быть получены путем попарных пересечений таксонов первого уровня и т.д. Количество таксонов на первом уровне определяется суммарной мощностью доменов значений признаков

Общее число уровней в комбинативной классификации равно количеству признаков.

Как видно из рис. 6,структура таксонов комбинативной классификации по отношению включения не является иерархической. Если рассматривать структуру связеймеждуотдельными фасетами, то получим булеву алгебру.

F

Рис. 6.Фасетная классификационная система

Архетипы классов комбинативной классификации представляют собой подмножество множества пар {(А_i, а_jⁱ)} имен и значений признаков. Для рассмотренного выше примера архетипами классов второго уровня будут множества:

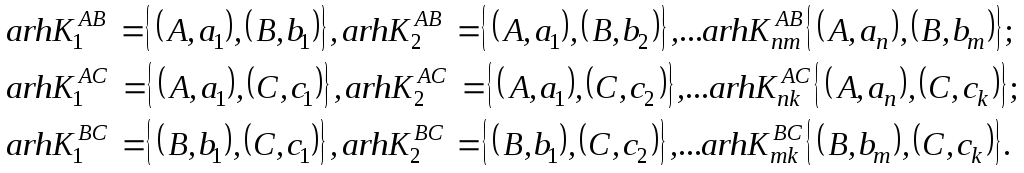
В качестве примера рассмотрим комбинативную классификацию множества сущностей {e₁, e₂, е₃, e₄, e₅, e₆, e₇, e₈},содержащих признаки с именами А, В, С,Dи значениямиdomА ={a₁, а₂, а₃},domВ ={b₁, b₂},domС = {c₁,c₂,c₃} иdomD= {d₁,d₂,d₃,d₄}.

Пусть значения признаков по сущностям распределены следующим образом:

e₁ = (a₁, b₁, c₁, d₁), е₂ = (a₁, b₁, c₂, d₁),

е₃ = (a₁, b₂, c₁, d₃), е₄ = (a₁, b₃, c₂, d₃),

e₅ = (а₂, b₂, c₁, d₄), е₆ = (а₂, b₃, c₁, d₄),

е₇ = (а₂, b₃, c₂, d₄), e₈ = (а₂, b₃, c₁, d₂).

Тогда классификационная решетка рассматриваемой предметной области может быть представлена в виде рис. 7.На первом уровне решетки находятся таксоны, которые определяются одиночными значениями признаков, на втором -они определяются парными комбинациями признаков, на третьем -тройками значений признаков.

Таксон Т₀содержит сущности, принадлежащие всей ПО, так как на него не накладывается никаких ограничений, а таксонT^ABCDпуст вследствие того, что в ПО отсутствуют сущности, обладающие всеми допустимыми значениями признаков одновременно. Отметим также, что в классификационной решетке отсутствуют классы сущностей первого уровня со значениями свойств b₁и b₂,так как о множествах объектов {e₁, e₂}и {е₃,e₅} можно сделать более точное утвержцение, чем то, что эти классы сущностей обладают свойствами b₁ и b₂.Действительно, таксонT₁содержит сущности, обладающие как признаком b₁,так и признаком a₁,а таксонT₁ –сущности, имеющие признаки b₂и C₁.Множества {e₁, e₂}и {е₃, е₅}, выделенные на основании только одного признака b₁или b₂,являются не классами, а предклассами. При свершении некоторых событий предклассы могут переходить в класс и, наоборот, классы могут превращаться в предклассы.

Отметим, что третий уровень классификационной решетки фактически содержит информацию, совпадающую с признаками ПО, за исключением таксона Т₆, в который попали сущностиe₆иe₈, не различимые на основании классификационных признаков с именами А, В и С, но имеющие различные характеристические признаки: сущностьe₆имеет свойствоd₄, а сущностьe₈ –признак d₂.

В работе показано, что для рассматриваемого множества таксонов классификационной решетки могут быть выделены таксоны -образующие, позволяющие путем выполнения над ними теоретико-множественной операции пересечения получить все остальные таксоны решетки.

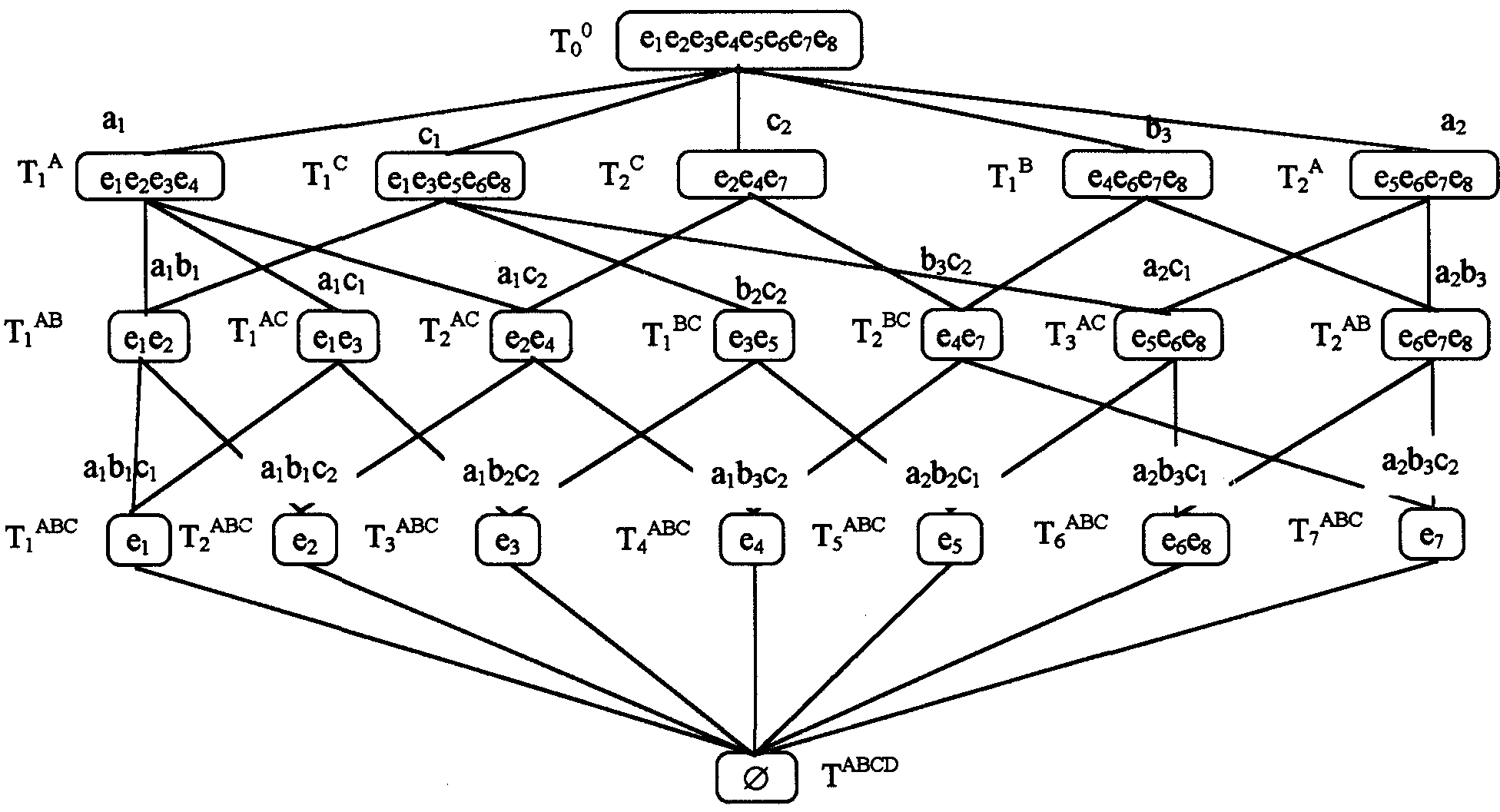
Рис. 7.Пример классификационной решетки гипотетической ПО

Из рис. 7видно, что в качестве классов-образующих для классификационной решетки необходимо взять таксоныT₁^A,T₁^C,Т₂^C,T₁^B,Т₂^A,T₁^AB,T₁^BC.

Очевиден и общий алгоритм выделения классов-образующих. Для этого достаточно к классам первого уровня решетки присоединить те классы более низких уровней, которые получены из предклассов первого уровня, чтобы получить искомый класс.

Комбинативные классификации имеют ряд преимуществ перед иерархическими классификациями, обеспечивая многоаспектное классифицирование информации, возможность произвольного комбинирования классификационных признаков, большую глубину понятий и возможность гибкого включения новых признаков.