1.3. Машина вывода

1.3.1. Понятие формальной системы

Прежде чем мы сформулируем понятие машины вывода, нам необ­ходимо дать определение формальной (аксиоматической) системы и правил вывода. Под формальной системой понимается четверка:

М = <Т, Р, А, П>, (1.10)

где Т - множество базовых элементов;

Р - множество правил построения правильных (сложных) объектов из базовых элементов;

А - множество изначально заданных объектов формаль­ной системы (множество аксиом );

П - множество правил построения новых объектов из других правильных объектов системы.

Для того, чтобы выяснить смысл этих формализмов, рассмотрим введенную ранее логическую модель как пример аксиома­тической системы.

В качестве множества базовых элементов Т здесь используются эле­менты языка логики предикатов: переменные, константы, функциональ­ные и предикатные символы и вспомогательные знаки.

В качестве множества правил Р построения правильных (сложных) объектов логики предикатов выступают правила построения формул логики предикатов.

Например, следующая формула является правильно построенной

(x(y( z( P(x, y) (z))))),

в то время как объект ниже

(x P(x, y))  (z((z)))

не является правильно построенной формулой.

Множество аксиом - это множество формул, истинность которых постулируется без доказательства.

Постулаты логики предикатов имеют вид схем аксиом. Схема аксиомы - это математическое выражение, которое дает конкретную ак­сиому каждый раз при подстановке вместо какой-то буквы одной и той же формулы.

Схемы аксиом логики предикатов таковы:

1. A  (B  A)

2. (A  B)  ((A  (B  C))  (A  C))

3. A  (B  A & B)

4. 1. A & B  A

   2. A & B  B

5. 1. A  A  B

   2. B  A  B

6. (A  C)  ((B  C)  (A  B  C))

7. (A  B)  ((A )A)

8. A

9.  x A(x)  A(t)

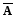10. A(t)  xA(x)

Постулаты арифметики:

1. A(o) & x (A(x)  A(x’))  A(x) (аксиома индукции)

2. a = b  a = b

3. a = b  (a = c  b = c)

4. A + 0 = a

5. a  0 = 0

6.

7. a = b  a = b

8. а + b = (а + b)

9. a b = a b + a

Здесь A,B,C- формулы; х - переменная;t- терм;a,b,c- целые числа; операция (’) (штрих) соответствует добавлению к числу единицы: а’ = а + 1.

Рассмотрим, например, схему аксиом (7). Заменим формулу А В наВ и подставим (7)

Далее по правилам де Моргана: =получаем:

Нетрудно видеть, что схема аксиом (7) является тождественно ис­тинной, если истинна формула A .

Мы, однако, не в состоянии доказать последнюю формулу, т.е. счи­таем ее истинной по определению.

Воспользуемся примером, иллюстрирующим это положение.

Рассмотрим высказывание "последовательность 0123456789 встре­чается в разложении числа ". Обозначим это высказывание через А. Тогда обратное высказываниеозначает, что "последовательность 0123456789 не встречается в разложении числа". Для того, чтобы доказать формулу А (или) в принципе нужно строить бесконечное представление для числа. Поскольку ни один шаг такого "доказа­тельства", если он не приводит к отысканию требуемой последовательности, не является законченным, мы не вправе считать, что до­казана формула А (). Итак, мы в принципе не в состоянии укачать финитное (конечное) доказательство ни для формулы А, ни для формулы.

Будем записывать десятичное разложение числа  , а под ним деся­тичную дробь= 0,333.... При записи каждой очередной цифры в разложениидобавляем "3" в. Если окажется, что высказывание А истинно, то стираем записанное представление дляи полагаем

где k- число троек, полученных в представлении к данному моменту.

Допустим, что справедлива формула В, где В - это высказывание "число рационально", и- обратное высказывание, т.е. число не рационально.

Спросим себя, рационально ли или нет? Еслине рационально (верно), то должно быть верно(иначе, если бы была получена последовательность 0123456789), то

где х, у - целые, т.е. было бы рационально. Однако, если справедливо , то= 1/3 = 0.333... (бесконечная последовательность). Здесьра­ционально, что противоречит предположению о его нерациональ­ности. Итак,не может быть не рациональным. Но значитрационально. Для этого однако, нужно иметь доказательство А или, чего у нас нет.

Действительно, если рационально либо мы построили беско­нечную последовательность 0,333... (что невозможно), либо доказали формулу А.

Приведенный пример характеризует так называемое интуицио­нистское направление в математике. Так интуиционисты отрицают правило tertiumnondatyr(третьего не дано). Ими также подвергается критике само понятие отрицания: ложность любой формулытрак­туется ими так, что допущениеведет к противоречию.

Еще один философский пример того же рода демонстрирует так называемый парадокс лжеца: "если некто говорит, что он лжет, то говорит ли он на самом деле правду или лжет?"

Обозначим высказывание "Я лгу " через А. Если А истинно, то "некто в действительности лжет", т.е. должно быть и наоборот. А это означает, что формулаA ни истинна, ни ложна (противоречива).

Вернемся, однако, к истине (1.10). Нам осталось определить пра­вила вывода П. Каждое правило вывода имеет структуру вида:

(1.13)

означающую, что если выведены формулы ₁,₂, ...,_n, называемые по­сылками, то выводима также формуланазываемая заключением.

Под выводимостью формулы из формул₁,₂, ...,_n, понимается такое отношение между этими формулами, что всякий раз, когда истин­на каждая из формул₁,₂, ...,_n, истинна также формула.

По определению, аксиома имеет структуру

,(1.14)

т.е. невыводима из других формул (множество посылок пусто).

Отметим следующие основные свойства для отношения выводимости.

1. Рефлективность:

(1.15)

2. Транзитивность:

(1.16)

(если выводима изи извыводима, то извыводима формула).

3. Монотонность:

(1.17)

(если из выводима формула, то присоединение кформулыне от­меняет выводимость). Отметим, что свойство монотонности в общем случае не имеет места в некоторых неклассических логиках, рассматри­ваемых в главе 3.

4. Теорема дедукции:

Если из ивыводима формула, то извыводима формула(- импликация).

(1.18)

Верна также обратная теорема:

(1.19)

Теорема дедукции имеет весьма важное значение в логике. Действи­тельно, чтобы доказать выводимость

(1.20)

заменим формулу эквивалентной формулой, где- символ пус­той формулы (лжи). Используя эквивалентную замену, по­лучим





 .(1.21)

Т





аким образом, установлен следующий важный факт: «для доказательства выводимости следует показать, что, т.е., что изиследует противоречие - .

В качестве основных правил вывода в логике предикатов используются правила modusponensиgeneralization.

Правило modusponens:

(1.22)

утверждает, что если истинны формулы А и А В, то истинна формулаB.

Правило generalization:

.(1.23)

Справедлива и обратное

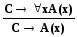(1.24)

при условии, что С не содержит переменной. х. Это последнее правило существенно важно при реализации наиболее широко применяемого резолютивного вывода, с содержанием которого мы познакомимся позднее.

В частности, если С пустая формула, то имеет место

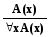(1.25)

Пример правила generalization:

Отметим, что правила вывода в логике предикатов не исчерпывают множества всех известных правил вывода. Однако, правила вывода име­ют иное семантическое содержание. Об этом следующий параграф.