
- •Содержание
- •Введение
- •Тематический план
- •Планы практических занятий
- •Занятие 7. Тема 4. Обобщающие статистические показатели
- •Общие положения, методический инструментарий и задания на практические занятия по темам
- •Тема 1. Методические основы статистики (2 ч.)
- •Основные положения темы
- •Вопросы и задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 2. Статистическое наблюдение (2 ч.) Основные положения темы
- •Иллюстративный материал темы к вопросу: формы, виды и способы наблюдения
- •Организационные формы
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 3. Сводка и группировка статистических данных (4 ч.) Основные положения темы
- •Методический материал и примеры решения типовых задач к вопросу: сущность и классификация статистических группировок
- •Пример группировки данных
- •Выполнение задания
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 4. Обобщающие статистические показатели (10 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: абсолютные величины Пример расчета условно-натуральных величин
- •К вопросу: относительные величины
- •Пример расчета относительных величин динамики
- •Пример расчета относительных величин планового задания
- •Пример расчета относительных величин выполнения планового задания
- •Пример расчета показателей, основанного на взаимосвязи относительных величин динамики, планового задания и выполнения плана
- •Пример расчета относительной величины структуры
- •Пример расчета относительной величины координации
- •Пример расчета относительной величины сравнения
- •К вопросу: средние величины
- •Пример расчета средних величин по не сгруппированным и сгруппированным данным
- •Пример расчета средней гармонической простой
- •Пример расчета средней гармонической взвешенной
- •Примеры расчета средней геометрической простой
- •Пример расчета средней квадратической
- •Пример применения правила выбора формы средней величины качественного признака
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 5. Анализ рядов распределения (10 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: понятие рядов распределения
- •Пример расчета средней арифметической взвешенной величины методом моментов
- •К вопросу: мода и медиана
- •Пример расчета медианы
- •Пример расчета моды
- •К вопросу: показатели вариации
- •Пример расчета показателей вариации
- •Пример расчета дисперсии методом моментов
- •Пример расчета дисперсии методом разности
- •К вопросу: виды дисперсии. Правило сложения дисперсии. Понятие эмпирического коэффициента детерминации и эмпирического корреляционного отношения
- •Пример расчета общей, межгрупповой и внутригрупповой дисперсии, эмпирического коэффициента детерминации и эмпирического корреляционного отношения
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 6. Анализ концентрации, дифференциации
- •Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: показатели дифференциации распределения
- •Пример расчета квартилей
- •Пример расчета децилей
- •Пример расчета квартильного и децильного коэффициентов
- •К вопросу: показатели концентрации распределения
- •Пример расчета коэффициента концентрации Джини
- •Пример расчета коэффициентов концентрации Герфиндаля и Розенблюта
- •К вопросу: понятие о закономерностях распределения
- •Пример расчета критериев согласия
- •К вопросу: показатели формы распределения
- •Пример расчета показателей формы распределения
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 7. Статистические методы измерения взаимосвязей (8 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: метод сравнения параллельных рядов
- •Пример оценки характера связи между показателями параллельного ряда с помощью коэффициента Фехнера
- •Пример оценки характера связи между показателями параллельного ряда с помощью коэффициента корреляции рангов Спирмена
- •Пример оценки характера связи между показателями параллельного ряда с помощью коэффициента корреляции рангов Спирмена в случае совпадения их значений
- •К вопросу: метод аналитической группировки. Понятие таблиц взаимной сопряженности
- •Пример расчета эмпирического корреляционного отношения
- •Пример оценки степени надежности эмпирического корреляционного отношения с помощью критериев Фишера и Стьюдента
- •К вопросу: показатели тесноты связи между двумя атрибутивными признаками
- •Пример расчета показателей тесноты связи между атрибутивными признаками
- •Пример расчета коэффициента взаимной сопряженности Чупрова
- •К вопросу: понятие корреляционно-регрессионного анализа
- •К вопросу: парная линейная регрессия
- •Пример построения уравнения парной линейной регрессии
- •Пример расчета коэффициентов эластичности
- •Пример расчета индекса корреляции (теоретического корреляционного отношения), коэффициента детерминации, линейного коэффициента корреляции и критериев Фишера и Стьюдента
- •К вопросу: понятие многофакторного корреляционно-регрессионного анализа
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 8. Анализ интенсивности динамики (4 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: общая характеристика рядов динамики
- •Пример смыкания рядов динамики данных, отличающихся друг от друга по числу включаемых в исследуемую совокупность единиц
- •Пример смыкания рядов динамики данных, отличающихся друг от друга методикой расчета показателей
- •К вопросу: статистические характеристики рядов динамики
- •Пример расчета показателей интенсивности динамики
- •Пример расчета среднего уровня полного интервального ряда динамики
- •Пример расчета среднего уровня неполного интервального ряда динамики
- •Пример расчета среднего уровня полного моментного ряда динамики
- •Пример расчета среднего уровня неполного моментного ряда динамики
- •Пример расчета средних показателей интенсивности динамики
- •К вопросу: сравнительный анализ рядов динамики
- •Пример сравнительного анализа рядов динамики
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 9. Анализ тенденции развития и колебаний (6 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: структура ряда динамики
- •К вопросу: изучение основной тенденции развития
- •Этапы изучения основной тенденции развития
- •1. Ряд динамики проверяется на наличие тренда
- •2. Производится выравнивание временного ряда
- •Пример проверки ряда динамики на наличие тренда
- •Пример проверки ряда динамики на наличие тренда с помощью метода серий
- •К вопросу: механическое выравнивание рядов динамики Пример механического выравнивания ряда динамики методом укрупненных интервалов
- •Пример механического выравнивания ряда динамики методом скользящей средней
- •К вопросу: аналитическое выравнивание рядов динамики
- •Пример аналитического выравнивания ряда динамики
- •К вопросу: характеристика колеблемости
- •К вопросу: сезонные колебания
- •Пример расчета индексов сезонности при условии отсутствия четко выраженной тенденции изменения уровней ряда динамики
- •Пример расчета индексов сезонности при условии наличия тренда
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 10. Индексный метод (8 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: общая характеристика статистических индексов
- •К вопросу: агрегатный индекс как основная форма общего индекса
- •Пример расчета индивидуальных и агрегатных индексов
- •К вопросу: общие индексы как средние из индивидуальных индексов
- •Пример расчета общих индексов как средних из индивидуальных индексов
- •10.4 Системы взаимосвязанных индексов
- •Пример взаимосвязи индексов и расчета величины абсолютного прироста результативного признака за счет изменения признаков-факторов
- •К вопросу: индексы с постоянной и переменной базой сравнения
- •Пример расчета цепных и базисных индексов физического объема, цен и товарооборота
- •К вопросу: индексы средних величин
- •Пример анализа относительного и абсолютного изменения средних значений качественного признака, в том числе за счет изменения соответствующих факторов
- •К вопросу: территориальные индексы
- •Пример расчета территориальных индексов
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 11. Выборочный метод (4 ч.) Основные положения темы
- •Индивидуальный
- •К вопросу: ошибки выборки
- •Пример расчета ошибок репрезентативности показателей выборки
- •Пример расчета средних ошибок выборки
- •Пример расчета предельных ошибок выборки и доверительных интервалов для характеристик генеральной совокупности
- •К вопросу: определение численности выборки
- •Пример расчета численности выборки, обеспечивающей заданную точность результатов исследования, формируемой посредством случайного бесповторного отбора
- •Пример расчета численности стратифицированной выборки, а также границ, в которых находится среднее значение признака единицы генеральной совокупности
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 12. Представление статистических данных:
- •Основные положения темы
- •Иллюстративный материал темы к вопросу: статистические таблицы
- •К вопросу: классификация статистических графиков
- •Вопросы и задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Список рекомендуемой литературы
- •98309 Г. Керчь, Орджоникидзе, 82
К вопросу: понятие корреляционно-регрессионного анализа
Теоретические
значения результативного признака
обычно обозначаются
![]() (читается:
«игрек, выровненный по икс») и
рассматриваются как функция от х,
т.е.
(читается:
«игрек, выровненный по икс») и
рассматриваются как функция от х,
т.е.
![]() .
Иногда для простоты записи вместо
пишут
.
Иногда для простоты записи вместо
пишут
![]() или
или![]() .
.
Для аналитической связи между х и у используются следующие виды уравнений:
-
![]() (прямая);
(прямая);
-
![]() (парабола второго порядка);
(парабола второго порядка);
-
![]() (гипербола);
(гипербола);
-
![]() (показательная или экспоненциальная
функция);
(показательная или экспоненциальная
функция);
-
![]() (логарифмическая функция) и др.
(логарифмическая функция) и др.
К вопросу: парная линейная регрессия
Парная линейная зависимость выражается при парной корреляции уравнением прямой:
, (7.20)
где – выровненное среднее значение результативного признака;
х – значение факторного признака;
а0 и а1 – параметры уравнения;
а0 – значение у при х = 0;
а1 – коэффициент регрессии.
Параметры уравнения связи определяются способом (методом) наименьших квадратов (МНК) с помощью составленной и решенной системы двух уравнений с двумя неизвестными:
 (7.21)
(7.21)
где n – число членов в каждом из двух сравниваемых рядов (число единиц совокупности);
∑x – сумма значений факторного признака;
∑x2 – сумма квадратов значений факторного признака;
∑y – сумма значений результативного признака;
∑yx – сумма произведений значений факторного признака на значения результативного признака.
Решив систему уравнений, получаем значения параметров уравнения связи, определяемые по формулам
 ;
(7.22)
;
(7.22)
 .
(7.23)
.
(7.23)
Если параметры уравнения определены правильно, то ∑у = ∑ .
Пример построения уравнения парной линейной регрессии
По данным таблицы 7.13 необходимо построить линейное уравнение связи, характеризующее зависимость выпуска продукции десяти предприятий одной отрасли от стоимости основных производственных фондов.
Таблица 7.13 - Данные, характеризующие 10 предприятий одной отрасли
Номер предприятия |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Стоимость ОПФ, млн. грн. |
12 |
8 |
10 |
6 |
9 |
15 |
11 |
13 |
14 |
10 |
Выпуск продукции, млн. грн. |
5,6 |
4,0 |
4,0 |
2,4 |
3,6 |
5,0 |
4,6 |
6,5 |
7,0 |
4,5 |
Для расчета параметров уравнения регрессии и выровненных по х значений у построим вспомогательную таблицу 7.14.
Таблица 7.14 - Данные, используемые для расчета параметров линейного уравнения связи стоимости основных производственных фондов и выпуска продукции 10 предприятий отрасли
№ завода (n) |
Стоимость ОПФ (х), млн. грн. |
Выпуск продукции (у), млн. грн. |
x2 |
xу |
у2 |
|
1 2 3 4 5 6 7 8 9 10 |
12 8 10 6 9 15 11 13 14 10 |
5,6 4,0 4,0 2,4 3,6 5,0 4,6 6,5 7,0 4,5 |
144 64 100 36 81 225 121 169 196 100 |
67,2 32,0 40,0 14,4 32,4 75,0 50,6 84,5 98,0 45,0 |
31,36 16,00 16,00 5,76 12,96 25,00 21,16 42,25 49,00 20,25 |
5,2 3,5 4,4 2,7 4,0 6,5 4,8 5,6 6,1 4,4 |
Всего |
108 |
47,2 |
1236 |
539,1 |
239,74 |
47,2 |
В среднем на 1 завод |
10,8 |
4,72 |
123,6 |
53,91 |
23,974 |
х |
По формуле 7.22
параметр уравнения прямой
![]() .
.
По формуле 7.23
коэффициент регрессии
![]() .
.
По формуле 7.20 линейное уравнение связи между стоимостью основных производственных фондов и выпуском продукции имеет вид: .
Коэффициент регрессии а1 = 0,421 показывает, что при увеличении стоимости основных производственных фондов на 1 млн. грн. выпуск продукции в среднем увеличится на 0,421 млн. грн.
Последовательно
подставляя в полученное уравнение
значения факторного признака х,
находим выровненные значения
результативного признака
![]() ,
показывающие, каким теоретически должен
быть средний размер выпущенной продукции
при данном размере основных производственных
фондов (при прочих равных условиях).
Выровненные (теоретические) значения
выпуска продукции приведены в последней
графе таблицы 7.14.
,
показывающие, каким теоретически должен
быть средний размер выпущенной продукции
при данном размере основных производственных
фондов (при прочих равных условиях).
Выровненные (теоретические) значения
выпуска продукции приведены в последней
графе таблицы 7.14.
Правильность расчета параметров уравнения подтверждает равенство ∑у = ∑ (47,2 = 47,2).
На рис. 7.3 представлены эмпирические, теоретические и средние уровни выпуска продукции предприятий отрасли, отличающихся по стоимости основных производственных фондов.
Выпуск продукции, млн. грн.



 7 -
7 -

6 -
 5 -
5 -

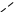


 4 -
4 -
3 -
2 -
1 -

 0 //
0 //
5 6 7 8 9 10 11 12 13 14 15 Стоимость ОПФ,
млн. грн.
 -
эмпирические уровни (у);
-
эмпирические уровни (у);
- теоретические уровни ( );
 -
средние уровни (
-
средние уровни (![]() ).
).
Рисунок 7.3 - Графическое изображение фактической и теоретической связи стоимости
основных производственных фондов и выпуска продукции 10 предприятий отрасли
Коэффициент эластичности для линейной зависимости (ε) определяется:
- для отдельной единицы совокупности по формуле
![]() ;
(7.24)
;
(7.24)
- в целом для совокупности по формуле
![]() .
(7.25)
.
(7.25)
