
- •Содержание
- •Введение
- •Тематический план
- •Планы практических занятий
- •Занятие 7. Тема 4. Обобщающие статистические показатели
- •Общие положения, методический инструментарий и задания на практические занятия по темам
- •Тема 1. Методические основы статистики (2 ч.)
- •Основные положения темы
- •Вопросы и задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 2. Статистическое наблюдение (2 ч.) Основные положения темы
- •Иллюстративный материал темы к вопросу: формы, виды и способы наблюдения
- •Организационные формы
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 3. Сводка и группировка статистических данных (4 ч.) Основные положения темы
- •Методический материал и примеры решения типовых задач к вопросу: сущность и классификация статистических группировок
- •Пример группировки данных
- •Выполнение задания
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 4. Обобщающие статистические показатели (10 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: абсолютные величины Пример расчета условно-натуральных величин
- •К вопросу: относительные величины
- •Пример расчета относительных величин динамики
- •Пример расчета относительных величин планового задания
- •Пример расчета относительных величин выполнения планового задания
- •Пример расчета показателей, основанного на взаимосвязи относительных величин динамики, планового задания и выполнения плана
- •Пример расчета относительной величины структуры
- •Пример расчета относительной величины координации
- •Пример расчета относительной величины сравнения
- •К вопросу: средние величины
- •Пример расчета средних величин по не сгруппированным и сгруппированным данным
- •Пример расчета средней гармонической простой
- •Пример расчета средней гармонической взвешенной
- •Примеры расчета средней геометрической простой
- •Пример расчета средней квадратической
- •Пример применения правила выбора формы средней величины качественного признака
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 5. Анализ рядов распределения (10 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: понятие рядов распределения
- •Пример расчета средней арифметической взвешенной величины методом моментов
- •К вопросу: мода и медиана
- •Пример расчета медианы
- •Пример расчета моды
- •К вопросу: показатели вариации
- •Пример расчета показателей вариации
- •Пример расчета дисперсии методом моментов
- •Пример расчета дисперсии методом разности
- •К вопросу: виды дисперсии. Правило сложения дисперсии. Понятие эмпирического коэффициента детерминации и эмпирического корреляционного отношения
- •Пример расчета общей, межгрупповой и внутригрупповой дисперсии, эмпирического коэффициента детерминации и эмпирического корреляционного отношения
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 6. Анализ концентрации, дифференциации
- •Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: показатели дифференциации распределения
- •Пример расчета квартилей
- •Пример расчета децилей
- •Пример расчета квартильного и децильного коэффициентов
- •К вопросу: показатели концентрации распределения
- •Пример расчета коэффициента концентрации Джини
- •Пример расчета коэффициентов концентрации Герфиндаля и Розенблюта
- •К вопросу: понятие о закономерностях распределения
- •Пример расчета критериев согласия
- •К вопросу: показатели формы распределения
- •Пример расчета показателей формы распределения
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 7. Статистические методы измерения взаимосвязей (8 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: метод сравнения параллельных рядов
- •Пример оценки характера связи между показателями параллельного ряда с помощью коэффициента Фехнера
- •Пример оценки характера связи между показателями параллельного ряда с помощью коэффициента корреляции рангов Спирмена
- •Пример оценки характера связи между показателями параллельного ряда с помощью коэффициента корреляции рангов Спирмена в случае совпадения их значений
- •К вопросу: метод аналитической группировки. Понятие таблиц взаимной сопряженности
- •Пример расчета эмпирического корреляционного отношения
- •Пример оценки степени надежности эмпирического корреляционного отношения с помощью критериев Фишера и Стьюдента
- •К вопросу: показатели тесноты связи между двумя атрибутивными признаками
- •Пример расчета показателей тесноты связи между атрибутивными признаками
- •Пример расчета коэффициента взаимной сопряженности Чупрова
- •К вопросу: понятие корреляционно-регрессионного анализа
- •К вопросу: парная линейная регрессия
- •Пример построения уравнения парной линейной регрессии
- •Пример расчета коэффициентов эластичности
- •Пример расчета индекса корреляции (теоретического корреляционного отношения), коэффициента детерминации, линейного коэффициента корреляции и критериев Фишера и Стьюдента
- •К вопросу: понятие многофакторного корреляционно-регрессионного анализа
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 8. Анализ интенсивности динамики (4 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: общая характеристика рядов динамики
- •Пример смыкания рядов динамики данных, отличающихся друг от друга по числу включаемых в исследуемую совокупность единиц
- •Пример смыкания рядов динамики данных, отличающихся друг от друга методикой расчета показателей
- •К вопросу: статистические характеристики рядов динамики
- •Пример расчета показателей интенсивности динамики
- •Пример расчета среднего уровня полного интервального ряда динамики
- •Пример расчета среднего уровня неполного интервального ряда динамики
- •Пример расчета среднего уровня полного моментного ряда динамики
- •Пример расчета среднего уровня неполного моментного ряда динамики
- •Пример расчета средних показателей интенсивности динамики
- •К вопросу: сравнительный анализ рядов динамики
- •Пример сравнительного анализа рядов динамики
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 9. Анализ тенденции развития и колебаний (6 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: структура ряда динамики
- •К вопросу: изучение основной тенденции развития
- •Этапы изучения основной тенденции развития
- •1. Ряд динамики проверяется на наличие тренда
- •2. Производится выравнивание временного ряда
- •Пример проверки ряда динамики на наличие тренда
- •Пример проверки ряда динамики на наличие тренда с помощью метода серий
- •К вопросу: механическое выравнивание рядов динамики Пример механического выравнивания ряда динамики методом укрупненных интервалов
- •Пример механического выравнивания ряда динамики методом скользящей средней
- •К вопросу: аналитическое выравнивание рядов динамики
- •Пример аналитического выравнивания ряда динамики
- •К вопросу: характеристика колеблемости
- •К вопросу: сезонные колебания
- •Пример расчета индексов сезонности при условии отсутствия четко выраженной тенденции изменения уровней ряда динамики
- •Пример расчета индексов сезонности при условии наличия тренда
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 10. Индексный метод (8 ч.) Основные положения темы
- •Иллюстративно-методический материал и примеры решения типовых задач к вопросу: общая характеристика статистических индексов
- •К вопросу: агрегатный индекс как основная форма общего индекса
- •Пример расчета индивидуальных и агрегатных индексов
- •К вопросу: общие индексы как средние из индивидуальных индексов
- •Пример расчета общих индексов как средних из индивидуальных индексов
- •10.4 Системы взаимосвязанных индексов
- •Пример взаимосвязи индексов и расчета величины абсолютного прироста результативного признака за счет изменения признаков-факторов
- •К вопросу: индексы с постоянной и переменной базой сравнения
- •Пример расчета цепных и базисных индексов физического объема, цен и товарооборота
- •К вопросу: индексы средних величин
- •Пример анализа относительного и абсолютного изменения средних значений качественного признака, в том числе за счет изменения соответствующих факторов
- •К вопросу: территориальные индексы
- •Пример расчета территориальных индексов
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 11. Выборочный метод (4 ч.) Основные положения темы
- •Индивидуальный
- •К вопросу: ошибки выборки
- •Пример расчета ошибок репрезентативности показателей выборки
- •Пример расчета средних ошибок выборки
- •Пример расчета предельных ошибок выборки и доверительных интервалов для характеристик генеральной совокупности
- •К вопросу: определение численности выборки
- •Пример расчета численности выборки, обеспечивающей заданную точность результатов исследования, формируемой посредством случайного бесповторного отбора
- •Пример расчета численности стратифицированной выборки, а также границ, в которых находится среднее значение признака единицы генеральной совокупности
- •Вопросы и задания для самоконтроля
- •Практические задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Тема 12. Представление статистических данных:
- •Основные положения темы
- •Иллюстративный материал темы к вопросу: статистические таблицы
- •К вопросу: классификация статистических графиков
- •Вопросы и задания для самоконтроля
- •Перечень вопросов для тестового контроля
- •Список рекомендуемой литературы
- •98309 Г. Керчь, Орджоникидзе, 82
Пример расчета коэффициента концентрации Джини
По данным таблицы 4.5 следует оценить степень неравномерности распределения работников предприятия по уровню их заработной платы и концентрации значений заработной платы в отдельных группах работников предприятия.
Для расчета коэффициента концентрации Джини построим таблицу 6.1.
Таблица 6.1 - Данные для расчета коэффициента концентрации Джини
Группы работников по уровню заработной платы, грн. |
Середина интервала, грн. (xi) |
Число работников, чел. (fi) |
Удельный вес (частость) работников, % |
Накопленная частость, % (pi) |
xi ∙ fi, грн. |
di, % |
qi, % |
pi ∙ qi+1 |
pi+1 ∙ qi |
800 -1000 1000 -1200 1200 - 1400 1400 - 1600 1600 - 1800 1800 и выше |
900 1100 1300 1500 1700 1900 |
20 80 160 90 40 10 |
5,0 20,0 40,0 22,5 10,0 2,5 |
5,0 25,0 65,0 87,5 97,5 100 |
18000 88000 208000 135000 68000 19000 |
3,4 16,4 38,8 25,2 12,7 3,5 |
3,4 19,8 58,6 83,8 96,5 100,0 |
- 99 1465 5447 8444 9750 |
85 1287 5128 8171 9650 - |
Всего |
- |
400 |
100,0 |
- |
536000 |
100,0 |
- |
25205 |
24321 |
По формуле 6.7, с учетом того, что pi и qi были выражены в процентах,
G = (25205 – 24321): 10000 = 0,09,
что свидетельствует о достаточно равномерном распределения работников предприятия по уровню их заработной платы и незначительной концентрации значений заработной платы работников в отдельных группах.
Коэффициент Герфиндаля (H) рассчитывается по формуле
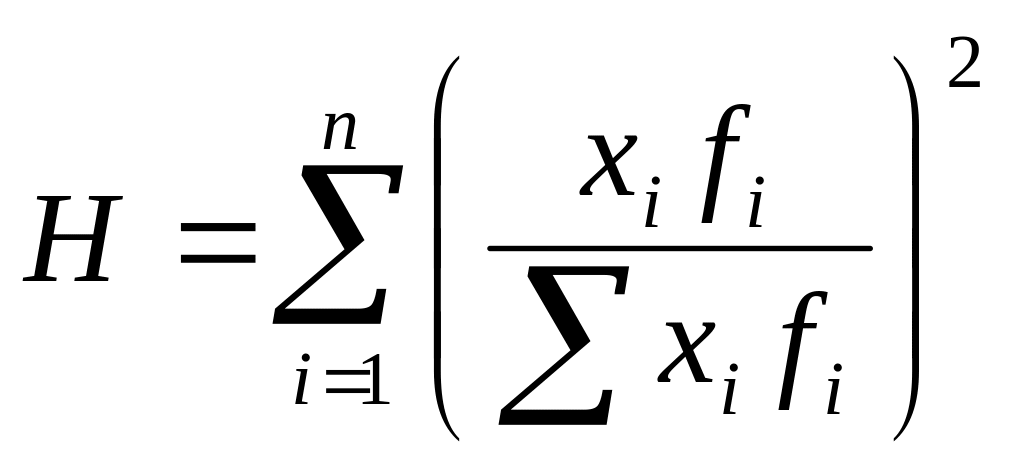 ,
(6.9)
,
(6.9)
где
![]() - доля значений признака i-ой
группы в общем объеме значений признака,
т.е. di,
рассчитываемое по формуле 6.8.
- доля значений признака i-ой
группы в общем объеме значений признака,
т.е. di,
рассчитываемое по формуле 6.8.
Интерпретация значения коэффициента Герфиндаля аналогична интерпретации значения коэффициента Джини.
Коэффициент Розенблюта (KR) рассчитывается по формуле
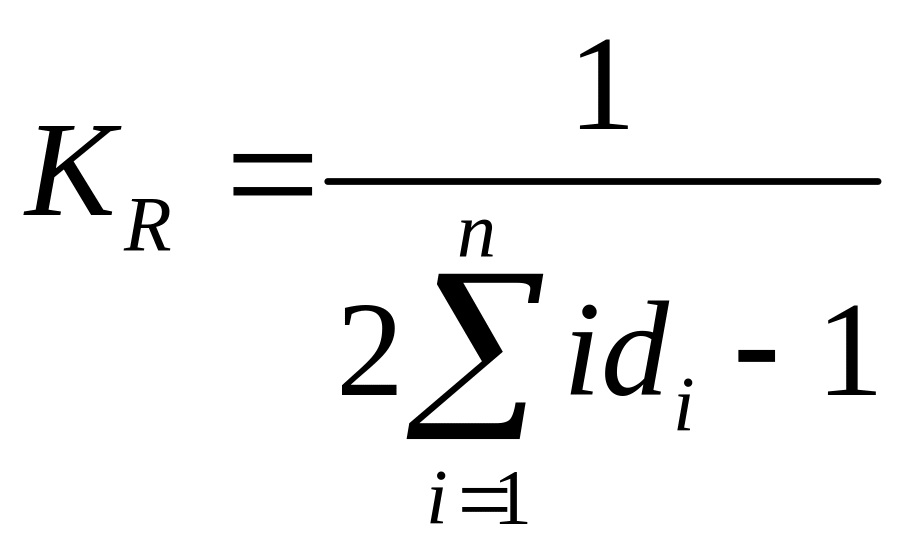 ,
(6.10)
,
(6.10)
где i – номер группы в совокупности;
di – доля i-ой группы в общем объеме совокупности;
n - число групп в совокупности.
Диапазон значений коэффициента Розенблюта 0 ≤ KR ≤ 1. При n = 1 и d1 = 1 KR = 1.
Пример расчета коэффициентов концентрации Герфиндаля и Розенблюта
По данным таблицы 5.5, используя данные таблицы 6.1, следует оценить степень концентрации значений заработной платы в отдельных группах работников предприятия с помощью коэффициентов Герфиндаля и Розенблюта. Для расчета коэффициентов концентрации построим таблицу 6.2.
Таблица 6.2 - Данные для расчета коэффициентов концентрации Герфиндаля и Розенблюта
Группы работников по уровню заработной платы, грн. |
Середина интервала, грн. (xi) |
Число работников, чел. (fi) |
xi ∙ fi, грн. |
di, выраженная в форме коэффициента |
т. е. di2 |
i
|
i ∙ di
|
800 -1000 1000 -1200 1200 - 1400 1400 - 1600 1600 - 1800 1800 и выше |
900 1100 1300 1500 1700 1900 |
20 80 160 90 40 10 |
18000 88000 208000 135000 68000 19000 |
0,034 0,164 0,388 0,252 0,127 0,035 |
0,0012 0,0269 0,1505 0,0635 0,0161 0,0012 |
1 2 3 4 5 6 |
0,034 0,328 1,164 1,008 0,635 0,210 |
Всего |
- |
400 |
536000 |
1,000 |
0,2594 |
- |
3,379 |
По формуле 6.9 коэффициент Герфиндаля H = 0,2594.
По
формуле 6.10 коэффициент Розенблюта
![]() .
.
Совместная интерпретация полученных значений коэффициентов Герфиндаля и Розенблюта позволяет сделать вывод об умеренной концентрации значений заработной платы в отдельных группах работников предприятия.

 ,
,