5.5.2. Сильноветвящиеся деревья

Еще одна группа сбалансированных деревьев поиска, которая использует другой способ поддержки сбалансированности, — сильноветвящиеся деревья. Напомним, что узлы сильноветвящихся деревьев могут иметь более двух сыновей, т. е. их нельзя отнести к бинарным деревьям. Однако принцип упорядоченности для сильноветвящихся деревьев аналогичен принципу, по которому строятся бинарные деревья поиска. А для того, чтобы обеспечить ветвление более чем по двум направлениям, узлам разрешено иметь более одного ключа.

Допустим, узел дерева имеет два ключа — 10 и 20. Такой узел может иметь максимум три сына — первый (крайний левый) должен иметь ключи, меньшие 10, второй — от 10 до 20 (10 входит в этот диапазон), третий (крайний правый) — более или равно 20.

На практике используются различные виды сильноветвящихся деревьев. В качестве структур для поиска в оперативной памяти применяются 2-3 деревья (их узлы имеют двух или трех сыновей) и 2-3-4 деревья (узлы могут иметь еще и четырех сыновей). Для поиска во внешней памяти наиболее подходят B-деревья, которые могут ветвиться еще сильней (B — balansed). B-деревья в настоящее время являются основными структурами для поиска в базах данных.

Различают две разновидности сильноветвящихся деревьев поиска. В первом случае все данные, в которых ведется поиск, располагаются только в листьях, а внутренние узлы содержат ключи-разделители, которые задают диапазоны ключей в поддеревьях и служат для выбора правильного направления движения по пути поиска. Во втором случае данные распределены по всем узлам.

В качестве примера рассмотрим структуру 2-3 дерева, в котором вся информация размещается в листьях [3]. Будем считать этот материал введением в сильноветвящиеся деревья поиска.

2-3 деревья

Пример 2-3 дерева изображен на рис. 5.14. Поскольку внутренние узлы могут содержать два ключа, на рисунке они изображены в виде прямоугольников, а листья, содержащие только один ключ, изображены, как обычно, в виде окружностей. Свойства 2-3 деревьев можно определить так.

1. Каждый лист содержит ключ и связанные с ним данные (на рисунке показаны только ключи). В графическом представлении 2-3 дерева ключи в листьях упорядочены слева направо.

2. Каждый внутренний узел содержит один или два ключа. Узел, содержащий один ключ, имеет двух сыновей, узел, содержащий два ключа, имеет трех сыновей.

3. Первым ключом внутреннего узла является ключ наименьшего из потомков второго сына (второй сын всегда есть, а его наименьший потомок может использоваться в качестве разделителя между первым и вторым поддеревом). Вторым ключом может являться ключ наименьшего потомка третьего сына, если третий сын есть. Тогда его наименьший потомок задает границу между вторым и третьим поддеревом.

4. Все листья располагаются на одном уровне. Исходя из этого условия, решается вопрос, сколько сыновей должен иметь каждый из внутренних узлов — два или три.

Добавим, что пустое дерево и дерево с одним корнем также являются 2-3 деревьями.

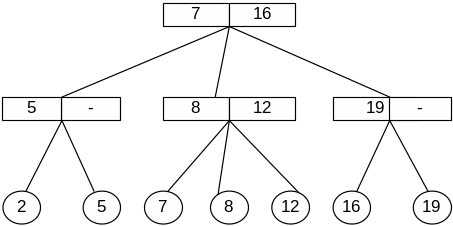
Рис.5.14. Пример 2-3 дерева

2-3-дерево с k уровнями может иметь от 2^k-1 до 3^k-1 листьев. Если в дереве n элементов, то дерево будет иметь от 1+log₃n до 1+log₂n уровней. Таким образом, длины всех путей имеют порядок O(log₂n).

Рассмотрим выполнение основных операций над 2-3 деревьями.

Поиск элемента в 2-3- дереве

Поиск выполняется аналогично поиску в бинарном дереве с той разницей, что для тех узлов, которые имеют два ключа, разветвление возможно по трем направлениям — к первому (левому), второму или третьему сыну, в зависимости от значения ключа. Например, для того, чтобы найти элемент с ключом 16 на рис.5.14, переходим от корня к его третьему сыну, а из этого узла переходим к первому сыну (он уже является листом и его ключ равен 16, поэтому поиск закончен успешно). При попытке найти ключ 18, будем двигаться по тому же самому пути, но, дойдя до листа, не обнаружим там значение 18, и поиск закончится промахом.

Вставка элемента в 2-3-дерево

Как обычно, сначала находим место, куда необходимо вставить новый элемент, двигаясь по пути поиска, как описано выше. Пусть мы уже спустились на уровень, непосредственно предшествующий листьям, и стоим в узле node. Далее возможны два варианта действий.

Если узел node имеет два сына, то делаем новый элемент третьим, помещая его в правильном порядке среди других сыновей, и изменяем значения ключей в родителе node. Например, на рис.5.15 показано добавление элемента с ключом 18 , к дереву ни рис.5.14. Больше никаких преобразований структуры не требуется, поскольку сбалансированность дерева не нарушена. Это простой случай.

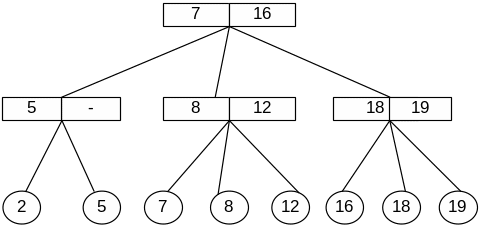
Рис. 5.15 Вставка элемента 18 в 2-3 дерево.

Второй случай сложнее. Если узел node уже имеет трёх сыновей, то новый добавляемый элемент становится четвертым сыном. Но четырех сыновей ни у одного узла 2-3 дерева быть не может. Поэтому выполняется операция, называемая расщеплением. Узел node раcщепляется на два узла node и node'. Два наименьших элемента из четырёх становятся сыновьями узла node, два наибольших – сыновьями узла node'. Теперь нужно вставить узел node' среди сыновей узла p – родителя узла node. Здесь ситуация аналогичная. Если p имеет два сына, то node' становится третьим и помещается непосредственно справа от node. Если узел p уже имеет трёх сыновей, то он расщепляется на да узла p и p', узлу p приписываются два наименьших сына, узлу p' – оставшиеся. Затем вставляем узел p' среди сыновей родителя узла p и т.д.

На рис.5.16 показан первый этап вставки элемента 10 в 1-2 дерево из рис.5.15, на котором произошло расщепление узла с ключами 8 и 12 на два узла. В полученном дереве корень имеет четырех сыновей, следовательно, потребуется расщеплять корень.

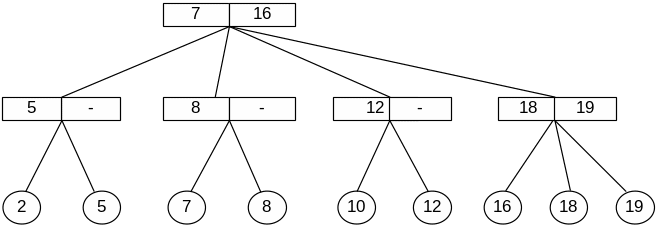
Рис.5.16. Вставка элемента 10 в 2-3 дерево — первый этап

В этой ситуации создаётся новый корень, чьими сыновьями будут два узла, полученные в результате разбиения старого корня. При этом число уровней дерева увеличивается на 1. Обратим внимание, что это единственная ситуация, когда высота дерева увеличивается, но сбалансированность не нарушается— все пути от корня до любого листа по-прежнему имеют одинаковую длину (рис.5.17).

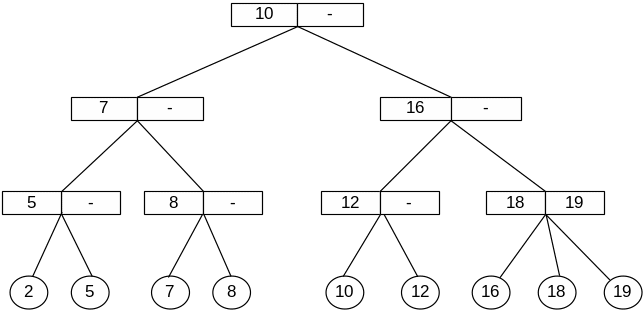
Рис.5.17. Вставка элемента 10 в 2-3 дерево — 2 этап (расщепление корня.)

Но в данной ситуации можно было бы обойтись без расщепления корня, если выполнить еще одну операцию над 2-3 деревьями, которая называется переливанием. Так, из рис.5.16 можно догадаться, что от одного из сыновей корня (это второй сын с ключом 8) можно избавиться, передав его первого сына левому брату, а второго сына— правому брату. Это возможно, поскольку у каждого брата только по два сына. Результат показан на рис.5.18.

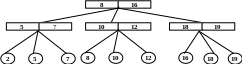
Рис.5.18. Вставка элемента 10 в 2-3 дерево — 2 этап (переливание узлов)

Однако при попытке вставить любое новое значение в дерево на рис. 5.18 все равно придется выполнять расщепление корня, и высота дерева увеличится на 1.

Удаление элемента из 2-3-дерева.

Если у родителя три листа, то удаление проблем не представляет. Например, из дерева на рис.5.18 можно удалить любой лист без какого-либо дополнительного преобразования структуры.

Рассмотрим случай, когда у узла два листа. Если узел является корнем, то единственный сын становится новым корнем дерева. Пусть node не является корнем. p – его родитель.

Если p имеет другого сына, расположенного слева или справа от node и имеющего трёх сыновей, то один из них становится сыном узла node. Это уже известная операция переливания.

Если сын p имеет только двух сыновей, то единственный сын узла node присоединяется к этим сыновьям, а узел node удаляется. Такая операция является обратной расщеплению и называется склеиванием. Если после этого родитель p будет иметь только одного сына, то повторяется вышеописанный процесс с заменой node на p.

Например, удалим элемент 10 из рис.5.17.

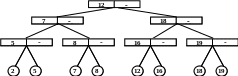
Рис.5.19. Удаление элемента 10 из 2-3 дерева из рис.5.17

В данном случае была выполнена операция переливания.

Теперь удалим из полученного дерева узел 7. Выполнив операции переливания и склеивания, получим дерево, изображенное на рис.5.20.

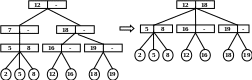
Рис.5.20. Удаление элемента 7 из 2-3 дерева из рис.5.19

Реализация вышеописанных операций не сложна, но трудоемка, поэтому здесь не приводится.