4.3.5. Нижняя оценка для алгоритмов сортировки, основанных на сравнениях

Все алгоритмы, рассмотренные в предыдущих разделах, относятся к классу сортировок, основанных на сравнениях. Говорят, что алгоритм сортировки основан на сравнениях, если он никак не использует внутреннюю структуру сортируемых элементов, а лишь сравнивает их и после некоторого числа сравнений выдаёт ответ (указывающий порядок элементов) [10].

Модель любого алгоритма, основанного на сравнениях, можно задать с помощью разрешающего дерева. Пример для сортировки вставками массива из трёх элементов представлен на следующем рис.4.11. Поскольку число перестановок из трёх элементов равно 3!=6, у разрешающего дерева 6 листьев.

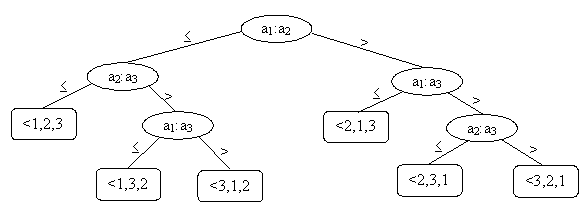
Рис. 4.11. Разрешающее дерево для алгоритма обработки вставками последовательности из трёх элементов [9].

Пусть мы сортируем n элементов a₁,…,a_n. Каждая внутренняя вершина разрешающего дерева соответствует операции сравнения и снабжена пометкой a_i:a_j, указывающей, какие элементы надо сравнивать. В каждом листе находится перестановка исходной последовательности, соответствующей ответу. Пути от корня до листьев соответствуют возможным последовательностям сравнений, выполняемых во время работы алгоритма.

Очевидно, что в результате работы алгоритма сортировки ответом может быть любая перестановка исходной последовательности, поэтому каждая из n! перестановок должна появиться хотя бы на одном листе.

Найдём нижнюю оценку для худшего случая. Число сравнений в худшем случае равно высоте разрешающего дерева – максимальной длине пути от корня до листа. Поскольку среди листьев представлены все перестановки n элементов, то их число не меньше n!. Поскольку двоичное дерево высоты h имеет не более 2^h листьев, то n!2^h. Логарифмируя это неравенство по основанию 2 и пользуясь неравенством n!>(n/e)ⁿ, вытекающим из формулы Стирлинга, имеем:

h  nlog n - nlog e = Ω(nlog n)

Таким образом, нижняя граница любого алгоритма сортировки, основанного на сравнениях, составляет Ω(nlog n).

Отсюда, в частности, следует, что алгоритмы сортировки слиянием и пирамидой являются асимптотически оптимальными.

4.4. Сортировка за линейное время

Как мы посмотрели в предыдущем параграфе, сортировки, основанные на сравнениях, не могут работать быстрее, чем за nlogn. Однако, если разрешить использование других операций – извлечение разрядов сортируемых элементов и использование их в качестве индексов, то можно добиться линейного времени работы.

4.4.1. Сортировка подсчетом

Алгоритм сортировки подсчетом (counting sort) применим, если сортируемые значения представляют собой целые положительные числа в известном диапазоне (не превосходящие заранее известного k).

В простейшем варианте алгоритм выглядит следующим образом. Создаётся вспомогательный массив с, размер которого совпадает с диапазоном возможных значений исходных чисел. Для каждого элемента x мы подсчитываем, сколько раз он встречается в исходной последовательности, используя в качестве счётчика элемент c[x]. Наконец, проходя по массиву c слева направо, выводим каждое число столько раз, сколько оно встречается. Пример реализации (все исходные элементы лежат в диапазоне [0,65535]):

void countSort(unsigned int a[], int n)

{

unsigned int c[65536];

memset(c,0,sizeof(c));

int i,j,k=0;

//подсчитываем, сколько раз встречается каждое число

for(i=0; i<n; i++) c[a[i]]++;

//формируем ответ

for(i=0; i<=65535; i++)

for(j=0; j<c[i]; j++)

a[k++] = i;

}

У описанного способа реализации имеется большой недостаток – его нельзя использовать для сортировки не самих числовых значений, а записей, содержащих эти значения в качестве ключей. Для того, чтобы это было возможным, логика работы алгоритма несколько изменяется. Первый шаг остаётся прежним – для каждого элемента мы подсчитываем в массиве c, сколько раз он встречается в исходной последовательности.

На следующем шаге мы проходим по массиву c и формируем в нём сумму с накоплением – т.е. после этого элемент c[x] будет содержать сумму всех элементов c, стоящих левее него. Смысл этого в том, что элемент c[x] будет содержать количество элементов, которые в результирующей последовательности стоят левее него.

На последнем шаге нам потребуется ещё один вспомогательный массив b для формирования результата. Проходя по исходному массиву, для каждого его элемента a[i] мы сразу определяем индекс в массиве b, где он должен оказаться: он равен c[a[i]]-1. При этом, поместив туда элемент, необходимо вычесть единицу из c[a[i]], чтобы следующий элемент с таким же значением поместился на нужное место.

При выполнении последнего шага есть одна особенность – для того, чтобы сортировка была устойчивой, исходный массив просматривается справа налево.

Пример реализации:

void countSort(unsigned int a[], int n)

{ unsigned int c[65536];

memset(c,0,sizeof(c));

int i,j;

//подсчитываем, сколько раз встречается каждое число

for(i=0; i<n; i++) c[a[i]]++;

//считаем сумму с накоплением

for(i=1; i<=65535; i++) c[i] += c[i-1];

//формируем ответ

unsigned int *b = new unsigned int[n];

for(i=n-1; i>=0; i--)

b[ --c[a[i]] ] = a[i];

memcpy(a,b,n*sizeof(unsigned int));

delete [] b;

}

Поскольку диапазон исходных значений ограничен константой, то как легко видно, время работы данного алгоритма составляет Θ(n).