5.4.1. Анализ алгоритмов поиска, вставки и удаления Поиск

На рис. 5.1 приведены четыре различных бинарных дерева одинаковой высоты, каждое из которых обладает свойством упорядоченности, поэтому принципиально может использоваться в качестве дерева поиска. Однако, даже без детального анализа алгоритмов видно, что не все из них могут обеспечить эффективный поиск. Проанализируем временную сложность алгоритма поиска для данных структур.

При изображении деревьев здесь и далее в узлах будем показывать только значения ключей (целые положительные числа), этого вполне достаточно для того, чтобы понять суть дела.

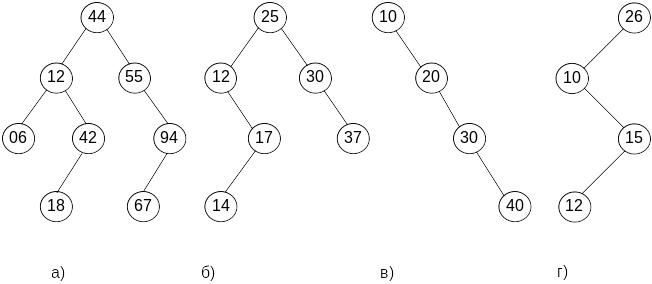
При достаточной плотности бинарного дерева поиска (рис.5.1,а) оно является очень удобной структурой быстрого поиска. Само название этого дерева, очевидно, связано с тем, что поиск нужного элемента можно выполнить кратчайшим путем. Двигаясь от корня к листьям и поворачивая при этом то вправо, то влево, мы в конце концов или найдем нужное значение ключа (попадание) или дойдем до пустой ссылки (промах). Путь, который был пройден до обнаружения попадания или промаха, назовем путем поиска.

Например, в дереве на рис.5.1,а значение 18 можно найти за 4 сравнения, при этом путь поиска пройдет через узлы с ключами 44 12 42 18 (последнее значение является искомым). Значение 55 будет найдено за 2 сравнения, а 44 (корень) будет обнаружено при первом же сравнении. При поиске значения 100 обнаружим промах за 3 сравнения, а при поиске числа 50 — промах за 2 сравнения.

При восьми узлах дерева это не так плохо, однако можно было бы получить и лучший результат (максимум 4 сравнения при 15 узлах), если бы бинарное дерево поиска оказалось полным (см. разд. 3.4). Действительно, высота полного бинарного дерева

h =log₂(n+1)-1,

т.е. в лучшем случае имеем логарифмическую сложность поиска, как для бинарного поиска в отсортированном массиве.

Для дерева на рис.5.1, б получаем результат похуже — для 6 узлов максимум 4 сравнения. И, наконец, на рис.5.1,в и 5.1,г представлены два самых худших варианта — вырожденные деревья, которые, по сути, ничем не отличаются от линейных списков, т. е. дают линейную сложность поиска.

Для того, чтобы избежать подобных крайне нежелательных ситуаций, на практике обычно используют так называемые сбалансированные деревья, высота которых специально поддерживается на своем нижнем уровне или близком к нему. Понятно, что сбалансированность дерева должна поддерживаться во время вставок и удалений элементов. Этому вопросу посвящен отдельный раздел, а сначала рассмотрим самые простые алгоритмы вставки и удаления, которые не гарантируют сбалансированной структуры дерева. Для нас они интересны тем, что с их помощью можно легко понять принципы работы с бинарными деревьями поиска, а затем использоваться их как основу алгоритмов для сбалансированных деревьев.

Для того, чтобы каждый раз отдельно не оговаривать лучший и худший случаи, будем оценивать сложность алгоритмов в зависимости от высоты дерева, а не от количества его узлов. Так, сложность алгоритма поиска можно оценить как

O(h), где h — высота бинарного дерева,

т. е. временная сложность поиска линейно зависит от высоты бинарного дерева поиска.