5.5. Сбалансированные деревья

Теперь можно перейти к обсуждению вопроса, как поддерживать бинарное дерево поиска в таком состоянии, которое полностью исключает наличие в нем длинных путей для поиска. Безусловно, самым идеальным вариантом для поиска является полное бинарное дерево, в котором каждый узел идеально сбалансирован, т. е. имеет одинаковое число потомков в правом и левом поддереве. При произвольном количестве узлов наиболее оптимальным для поиска является требование, чтобы все листья располагались в двух последних уровнях дерева. К сожалению, поддержка дерева в таком состоянии при выполнении каждой вставки или удаления требует значительных усилий. Если таблица изменяется достаточно интенсивно, то существенное замедление вставок и удалений сведет на нет весь выигрыш в скорости поиска.

Однако есть несколько способов поддержки дерева в хорошем (хоть и не идеальном) состоянии за приемлемое время вставки и удаления. Деревья, которые постоянно поддерживаются в состоянии, близком к наилучшему, с приемлемыми временными характеристиками вставки и удаления, получили название сбалансированных. Мы рассмотрим несколько видов таких деревьев. Наиболее изученными деревьями, которые поддерживают хорошее сбалансированное состояние, являются АВЛ-деревья.

5.5.1. АВЛ-деревья

Определение и свойства авл-деревьев

АВЛ-дерево названо в честь изобретателей этого метода Г.М. Адельсона-Вельского и E.М. Ландиса, которые дали ему следующее определение. Дерево называется АВЛ-деревом, если для любого его узла высоты левого и правого поддеревьев отличаются не более чем на 1. АВЛ-дерево называют сбалансированным по высоте.

Согласно определению, сбалансированность АВЛ-дерева должна проверяться для каждого его узла. С этой целью вводится дополнительная характеристика каждого узла, которая называется показателем сбалансированности узла или балансом узла. Этот показатель представляет собой разность между высотой правого и левого поддерева узла (сами высоты поддеревьев не важны, так как только разность является мерой сбалансированности). Для сбалансированного дерева этот показатель может принимать всего три значения (рис.5.4):

• 0— высоты поддеревьев равны;

• -1 — левое поддерево немного перевешивает;

• 1 — правое поддерево немного перевешивает.

Рис.5.4. Значения показателя сбалансированности

Здесь треугольниками разной высоты обозначены поддеревья узла (такое обозначение будет использоваться и в других рисунках).

На рис. 5.5 изображен пример АВЛ-дерева, из которого видно, что оно не соответствует идеальному состоянию сбалансированности, поскольку листья располагаются в трех нижних уровнях. Тем не менее, для всех узлов балансы находятся в допустимых пределах (балансы изображены сверху от каждого узла). Обратим внимание, что у всех узлов, которые имеют только одного сына, этот сын является листом, а все листья имеют нулевые балансы.

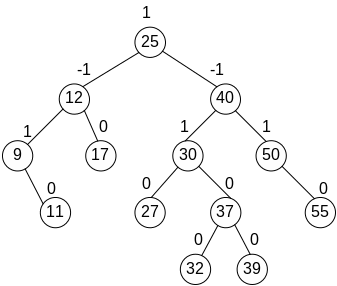
Рис.5.5. Пример АВЛ-дерева с расставленными балансами узлов

Авторами АВЛ-дерева доказано, что при наличии n узлов высота дерева находится в интервале от log₂(n+1)-1, что соответствует полному бинарному дереву, до 1,44log₂(n+2)-1,33 для наихудшего случая (доказательство приводится в [8, 21]). Иными словами, оно гарантированно обеспечивает время поиска, не превышающее наилучший случай более чем на 45%.

Замечательной особенностью АВЛ-деревьев является то, что это почти идеальное время поиска достигается незначительным усложнением алгоритмов вставки и удаления, которые по-прежнему могут быть выполнены с логарифмической временной сложностью.

Для восстановления состояния сбалансированности АВЛ-дерева при вставках и удалениях необходимо проверить балансы всех его узлов, и в случае недопустимых значений выполнить специальные операции, которые получили название вращений (другие названия — повороты, ротации, англ. rotations). Рассмотрим подробнее, что представляют собой вращения.