Анализ алгоритма сортировки бинарным деревом поиска
Оценим сложность построения бинарного дерева поиска.
Первая мысль, которая возникает при начальном знакомстве с этим методом — сильная зависимость структуры дерева от входных данных. Если данные абсолютно случайны (например, массив формировался при помощи датчика случайных чисел), то дерево получится достаточно плотным, как на рисунке 4.5. При построении такого дерева можно значительно выиграть во времени на сокращении количества сравнений при поиске места для каждого нового листа. В самом лучшем случае потребуется log2n сравнений на каждый добавляемый элемент, следовательно, временная сложность построения дерева из n элементов составит O(nlogn).
Но если входная последовательность уже была отсортирована, то дерево выродится в линейный список (перемещаясь по дереву, будем двигаться все время по одной ветви). Сам процесс построения вырожденного дерева потребует столько же времени, сколько и простые методы сортировки — O(n2). Для того, чтобы исключить возможность получения вырожденного дерева или дерева с низкой плотностью, можно хорошенько «перемешать» исходные данные перед тем, как их сортировать, но на это опять потребуется лишнее время.
Такое поведение алгоритма следует оценить как неестественное. Устойчивости также нет. Есть и еще один крупный недостаток этого метода - большие требования к памяти под дерево. Кроме места под значения элементов требуется память на 2 указателя для каждого из них.
В силу этих недостатков данный способ не находит практического применения в тех случаях, когда требуется просто отсортировать массив или список в оперативной памяти. Но не нужно забывать, что основное назначение бинарного дерева поиска — быстрый поиск данных. Поэтому, если бинарное дерево поиска строилось непосредственно при считывании данных с диска, чтобы затем использовать его для задач поиска, то это наилучший способ получить данные в отсортированном виде.
Подробно реализацию бинарного дерева поиска рассмотрим в следующей главе. Наибольшего внимания из древовидных методов заслуживает пирамидальная сортировка, поэтому рассмотрим ее подробнее.
4.3.2. Пирамидальная сортировка
В алгоритме пирамидальной сортировки используется специальная структура данных - пирамида (иногда её также называют кучей, англ. heap). Пирамидой называется двоичное дерево, в вершинах которого размещаются заданные нам элементы. При этом должны выполняться следующие требования:
все уровни, за исключением последнего, должны быть заполнены полностью
последний уровень (т.е. уровень листьев дерева) может быть заполнен частично, но обязательно слева направо без пропусков
основное свойство пирамиды: ни один элемент в пирамиде не может быть больше своего родителя
П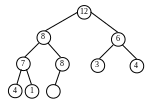
ример
пирамиды:
Рис. 4.6 Пирамида
Очевидно, что на вершине пирамиды находится наибольший её элемент.
Для представления пирамиды в памяти удобно использовать массив, при этом пирамида хранится в массиве следующим образом. Сыновья элемента с индексом i будут иметь индексы i*2+1 и i*2+2, а его родитель - индекс (i-1)/2 (напомним, что в языке C++ массивы начинаются с нуля, а при делении двух целых чисел дробная часть отбрасывается). Так, для вышеприведённого рисунка пирамида будет храниться в массиве следующим образом:
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
12 |
8 |
6 |
7 |
8 |
3 |
4 |
4 |
1 |
6 |
Рис. 4.7. Хранение пирамиды в массиве
Например, для элемента с индексом 3 сыновьями будут элементы с индексами 3*2+1=7 и 3*2+2=8, а родителем - элемент с индексом (3-1)/2=1.