3.8. Применения деревьев
Деревья находят применение в различных алгоритмах обработки данных, поэтому набор задач, которые можно выбрать в качестве примеров, весьма обширен. Учитывая, что такие важные направления применения как сортировка и поиск данных рассматриваются в следующих главах, в данном разделе рассмотрим два других очень распространенных применения. Первое из них — анализ выражений, записанных в виде формулы, второе относится к задаче сжатия информации.
3.8.1. Дерево-формула
Арифметические и логические выражения часто представляются в памяти при помощи дерева, которое получило название дерева-формулы. Возьмём в качестве примера выражение (2+4)*7-3/5. Тогда получим следующее бинарное дерево, изображенное на рис. 3.13.
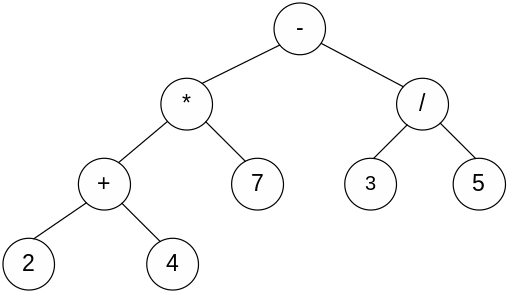
Рис.3.13. Пример дерева-формулы
Листья дерева-формулы — всегда операнды (переменные или значения), а все внутренние узлы соответствуют операциям.
Строго говоря, дерево-формулу правильнее отнести к упорядоченным деревьям из-за наличия унарных операций, т. к. в этом случае правое и левое поддерево не различаются. Но если в выражении присутствуют только бинарные операции, как в приведенном примере, то соответствующее дерево-формула представляет собой строго бинарное дерево.
Каждое поддерево дерева-формулы соответствует некоторой части исходного выражения, причем операцию, которая находится в корне этого дерева, можно выполнить только после вычисления значений поддеревьев. Например, для дерева, которое изображено на рис.3.12 операция умножения (корень левого поддерева) может быть выполнена только после того, как будет выполнена операция сложения (2+4). Операция, которая находится в корне дерева выражения, должна быть выполнена последней. В данном примере сначала вычисляется (2+4)*7, затем 3/5, а последней выполняется операция вычитания. Обратим внимание, что такой порядок вычисления соответствует обратному (восходящему) порядку обхода дерева.
Дерево-формула — классический пример для иллюстрации различных способов обхода деревьев. Одна из распространенных терминологий для названий обходов — префиксный (PreOrder, прямой порядок), постфиксный (PostOrder, обратный порядок) и инфиксный (InOrder, центрированный порядок). Эти названия связаны с различными формами представления дерева-формулы. Применяя различные методы обхода к дереву на рис.3.13, получим разные способы записи выражения:
- * + 2 4 7 / 3 5 префиксная форма
2 4 + 7 * 3 5 / - постфиксная форма
2 + 4 * 7 – 3 / 5 инфиксная форма
Как видим, во всех трех случаях порядок следования операндов один и тот же, разница только в порядке операций.
Центрированный порядок полностью соответствует обычной записи арифметического выражения, если из нее убрать скобки. По такой записи невозможно правильно вычислить значение выражения, не зная, как были расставлены скобки. Зато два других способа можно использовать для вычисления значения выражения непосредственно, т. к. в этом случае порядок вычислений определяется однозначно. Из приведенного примера видно, что при префиксной форме знак операции непосредственно предшествует своим операндам, при постфиксной форме он располагается сразу после операндов. В префиксной форме порядок выполнения операций следует читать справа налево (знак последней операции — крайний слева символ), в постфиксной — слева направо. Эти две формы иначе называются бесскобочными формами записи выражения.
Наиболее удобной в реализации является постфиксная форма, которая получила название обратной польской записи (ОПЗ), поскольку ее использование для представления выражений впервые предложил польский математик Я.Лукашевич. Она часто используется как промежуточная форма представления выражений во многих компиляторах и интерпретаторах. На это есть два соображения.
Вычисление выражения по ОПЗ можно выполнить итеративно за один проход.
Существует простой итеративный алгоритм, предложенный Дейкстрой, для перехода от арифметического выражения, записанного в обычной форме со скобками, к постфиксной форме [10].
Рассмотрим данный алгоритм подробнее, поскольку он является основой для решений многих задач обработки выражений. Суть его такова — исходная стpока-выражение просматривается слева напpаво, при этом опеpанды пеpеписываются в выходную стpоку, а знаки опеpаций заносятся во вспомогательный стек операций на основе следующих сообpажений:
если стек пуст, то опеpация из входной стpоки пеpеписывается в стек;
опеpация выталкивает из стека все опеpации с большим или pавным пpиоpитетом в выходную стpоку;
если очеpедной символ из исходной стpоки есть откpывающая скобка, то он пpоталкивается в стек;
закpывающая кpуглая скобка выталкивает все опеpации из стека до ближайшей откpывающей скобки, сами скобки в выходную стpоку не пеpеписываются, а уничтожают дpуг дpуга.
Пpоцесс получения обpатной польской записи для выpажения (A+B)*(C+D) схематично пpедставлен в табл. 3.8.
Таблица 3.8
Получение ОПЗ
Пpосматpиваемый символ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
Входная строка |
( |
A |
+ |
B |
) |
* |
( |
C |
+ |
D |
) |
- |
E |
|
Состояние стека |
( |
( |
+ ( |
+ ( |
|
* |
( * |
( * |
+ ( * |
+ ( * |
* |
- |
- |
|
Выходная строка |
|
A |
|
B |
+ |
|
|
C |
|
D |
+ |
* |
E |
- |
В листинге 3.9 реализован данный алгоритм.
Листинг 3.9. Перевод строки-выражения в постфиксную запись
#include <iostream.h>
#include <string.h>
#include <ctype.h>
#include "stack.h"
// вспомогательная функция priority возвpащает пpиоpитет опеpации
int priority(char a)
{ switch(a)
{case '*': case '/': return 3;
case '-': case '+': return 2;
case '(': return 1;
}
}
// перевод строки-выражения в постфиксную запись
void exprtopost(char *s_expr, char *s_post)
{stack<char> s; //вспомогательный стек символов
int k=0,p=0;
while(s_expr[k]!='\0')
{ if(s_expr[k]==')')// если очеpедной символ - ')'
//то выталкиваем из стека все знаки опеpаций до ближайшей '('
{while((s.gettop())!='(') s_post[p++]=s.pop();
s.pop(); //удаляем из стека саму откpывающую скобку
}
//если очеpедной символ - цифра, то записываем в вых. строку
if(isdigit(s_expr[k])) s_post[p++]=s_expr[k];
//если очеpедной символ - '(' , то заталкиваем её в стек
if(s_expr[k]=='(') s.push('(');
// Если следующий символ - знак опеpации
if(strchr("+-*/",s_expr[k]))
{// если стек пуст, записываем в него опеpацию
if(s.isnull()) s.push(s_expr[k]);
else // если не пуст
// если пpиоpитет поступившей опеpации больше
// пpиоpитета опеpации на веpшине стека
// заталкиваем поступившую опеpацию в стек
if(priority(s.gettop())<priority(s_expr[k]))s.push(s_expr[k]);
else // если пpиоpитет меньше
{ // пеpеписываем в выходную стpоку все опеpации
// с большим или pавным пpиоpитетом
while((!s.isnull())&&(priority(s.gettop())>=priority(s_expr[k])))
s_post[p++]=s.pop();
s.push(s_expr[k]);// заталкиваем в стек поступившую опеpацию
}
}
k++;//Пеpеход к следующему символу входной стpоки
}//конец цикла
// Пеpеписываем в вых. строку все оставшиеся опеpации из стека
while(!s.isnull()) s_post[p++]=s.pop();
s_post[p]='\0';
}
Полученную строку, содержащую ОПЗ, можно использовать для вычисления значения выражения. Более того, немного дополнив приведенный алгоритм, его можно использовать непосредственно для вычисления выражения без предварительного преобразования в ОПЗ. Для этого потребуется завести еще один вспомогательный стек, который будет служить для временного хранения операндов и промежуточных результатов. Это хорошее упражнение для самостоятельной работы.
Таким образом, префиксная и постфиксная формы записи выражения являются удобными способами представления дерева-формулы. Все же более универсальным способом обработки выражений является явное построение дерева-формулы. Имея такое дерево, можно решать широкий спектр задач, например, упрощение выражения, аналитическое дифференцирование формулы и т. д. Вычисление выражения также легко реализуется на основе обратного обхода дерева-формулы.
Имея постфиксную форму записи выражения, построить дерево-формулу сравнительно легко. Достаточно перевернуть ее слева направо, после чего за один проход такой строки можно построить дерево в порядке «корень - правое поддерево - левое поддерево», имея один вспомогательный стек для хранения указателей на узлы дерева.
С целью сокращения программного кода при реализации дерева-формулы примем следующие упрощения. Будем считать, что выражение содержит только цифры и 4 знака арифметических операций. Тогда в узлах дерева-формулы можно хранить символы (тип char), и построение дерева существенно упрощается за счет того, что практически отсутствует трудоемкая процедура выделения лексем — элементарных единиц, из которых состоит обычное, а не упрощенное выражение.
В листинге 3.10 приведена функция для построения дерева-формулы на основе постфиксной формы записи для случая упрощенного выражения, а также рекурсивная функция, которая вычисляет значение этого выражения, реализуя обратный обход построенного дерева-формулы. Обратим внимание, что в структуру, описывающую каждый узел дерева, добавлены конструктор, который позволит заполнять узел значениями в момент его создания, и деструктор для корректного освобождения памяти в конце работы программы.
Листинг 3.10. Реализация дерева-формулы
// структура дерева формулы, файл ft.h
struct node //тип узла дерева-формулы
{ char data; //символ (лексема)
node* left;
node* right;
node (char x)//добавим конструктор,
//который будет выполняться при создании узла
{data=x; left=right=NULL;}
~node () //и деструктор для освобождения памяти
{if (left) delete left;
if (right) delete right;
}
};
typedef node* ft;//указатель на узел-поддерево(ft-formula-tree)
// функции для работы с деревом формулой, файл ft.cpp
#include <iostream.h>
#include <string.h>
#include "stack.h"
#include "ft.h"
//функция построения дерева-формулы по постфиксной форме
ft posttotree(char* s_post)
{ strrev (s_post);// перевернули строку
stack<ft> s; char k;
ft root=new node(s_post[0]);//корень - первый символ
ft temp=root; // текущий указатель
s.push(root); //корень поместили на дно стека
for(int i=1;i<strlen(s_post);i++)
{ k = s_post[i]; //пеpеходим к анализу каждого символа
if (strchr("+-*/",k)) //символ - опеpация
{ if (!temp->right) //еще нет пpавого сына
{ temp->right = new node(k);// добавили его
temp = temp->right; //и установили на него указатель
}
else //есть пpавый сын
{ temp->left = new node(k); // добавили левого
temp = temp->left; //и установили на него указател
}
s.push(temp); //поместили указатель в стек
}
else //cимвол - опеpанд
{ if (!temp->right) //еще нет пpавого сына
temp->right = new node(k); //теперь уже есть
else //есть пpавый сын
temp->left = new node(k); //добавили левого сына
// Текущий указатель возвpащается вверх
if(s.gettop()!=root)temp=s.pop();//удаляем указатель из стека
else temp=s.gettop(); //если это не корень
}
} //конец цикла for
s.pop(); //удалили из стека корень
return root;
}
//вспомогательная функция для вычислений
float operation (char symbol, float operand1, float operand2)
{ float temp;
switch (symbol)
{ case '+': temp = operand1 + operand2; break;
case '-': temp = operand1 - operand2; break;
case '*': temp = operand1 * operand2; break;
case '/': temp = operand1 / operand2; break;
} return temp;
}
// вычисление выражения по дереву-формуле
float calc( ft t)
{ float opnd1,opnd2,rez=0; char symb;
if (t) // если дерево не пусто
{ if (strchr("+-*/",t->data)) //рекурсивная ветвь
{ opnd1 = calc (t->left);
opnd2 = calc (t->right);
symb = t->data;
rez = operation (symb,opnd1,opnd2);
}
else // терминальная ветвь
rez = t->data-48;//по ASCII-коду цифры вычисляем значение
return rez;
}
}