3.3. Бинарные деревья

3.3.1. Определение. Представления бинарных деревьев

Бинарное (двоичное) дерево — особый вид дерева, в котором каждый узел имеет не более двух поддеревьев, причем в случае одного поддерева следует различать левое и правое поддерево. При изображении бинарных деревьев левого и правого сына различают по наклону соединительной линии (влево или вправо). На рис.3.4 показаны два различных бинарных дерева. Интересно отметить, что если рассматривать данные структуры как обычные упорядоченные деревья, то они являются полностью идентичными (в упорядоченном дереве единственный сын всегда первый, т. е. левый потомок). Это говорит о том, что бинарные деревья не являются частным случаем упорядоченого дерева, а представляют собой особый вид деревьев.

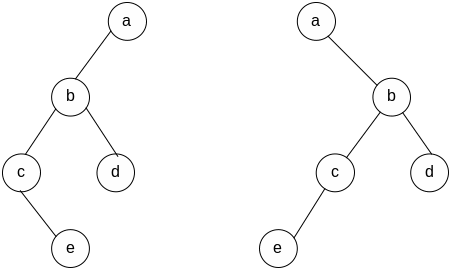
Рис.3.5. Два различных бинарных дерева

Приведем формальное рекурсивное определение бинарного дерева [8].

Бинарное дерево — конечное множество узлов, которое является пустым или состоит из корня и двух непересекающихся бинарных деревьев, которые называются левым и правым поддеревьями данного корня.

Обратим внимание на то, что бинарное дерево может быть пустым, в отличие от обычного дерева, которое всегда содержит хотя бы один узел (однако лес может быть пустым).

Бинарное дерево может быть представлено и в форме скобочного выражения. Аналогично обычному корневому дереву, для бинарного дерева также возможен различный порядок перечисления узлов в скобочном представлении. Например, левое скобочное представление непустого бинарного дерева рекурсивно определяется так:

(<корень> (<левое поддерево> <правое поддерево>))

Иногда при записи левое и правое поддерево разделяют запятыми, но чаще пробелом.

Левое или правое поддерево или оба вместе (для листьев) могут быть пустыми, при этом для пустых деревьев часто используется специальное обозначение . Чтобы сократить запись, в ней разрешается опустить правое поддерево, если оно пустое, а для листьев опустить оба пустых поддерева (но нельзя опускать пустое левое поддерево, иначе по такой записи нельзя будет правильно восстановить изображение бинарного дерева!). Так, деревьям, изображенным на рис.3.5, соответствуют различные левые скобочные записи в сокращенной форме:

( a ( b (c ( e) d ) ) )

( a (  b ( c ( e ) d ) )

Бинарные деревья, у которых все узлы, кроме листьев, имеют сторого по два сына, называются строго бинарными. Деревья, изображенные на рис. 3.5, не являются строго бинарными.

3.3.2. Математические свойства бинарных деревьев

Бинарные деревья, как абстрактные математические объекты, обладают рядом интересных свойств, которые могут пригодиться при анализе различных алгоритмов, поэтому остановимся подробнее на этом вопросе.

На любом уровне n бинарное дерево может содержать от 1 до 2ⁿ узлов. Число узлов, приходящееся на уровень, является показателем плотности дерева. На рис. 3.6 дерево А содержит 8 узлов при высоте 3, в то время как дерево B содержит 5 узлов при высоте 4.

Последний случай является особой формой, называемой вырожденным (degenerate) деревом, у которого есть единственный лист (e) и каждый внутренний узел имеет только одного сына. Вырожденное дерево можно считать аналогом линейного связного списка, его высота равна количеству узлов без единицы. Это максимально возможное значение для высоты бинарного дерева. В большинстве алгоритмов, использующих бинарные деревья, вырожденное дерево — наихудший случай при оценке производительности.

Рис.3.6. Бинарные деревья различной плотности

Наоборот, деревья с большой плотностью очень важны в качестве структур данных, так как они содержат пропорционально больше элементов вблизи корня, т.е. с более короткими путями от корня.

Наивысшей степенью плотности обладают полные бинарные деревья, которые имеют 2^k узов на каждом уровне k.

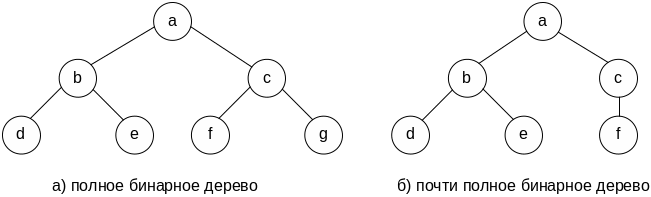
Рис.3.7. Полное и почти полное бинарные деревья

На рис. 3.7, а показано полное бинарное дерево высоты два. Обратим внимание на такие факты.

На нулевом уровне имеется 2⁰ узлов, на первом — 2¹, на втором — 2² и т.д. На первых k-1 уровнях количество узлов составляет

1 + 2 + 4 + ... + 2^k-1 = 2^k-1

На уровне k количество узлов 2^k, т. е. ровно на один больше.

Из этого следует, что в полном бинарном дереве количество внутренних узлов на единицу меньше количества листьев. Зная количество листьев, легко определить и высоту h полного бинарного дерева:

h=log ₂ n, где n — количество листьев

или

h= log ₂ (N+1)-1, где N —количество узлов полного бинарного дерева.

Для полного бинарного дерева приведенные формулы дают точное значение, сответствующее минимальному значению высоты при таком количестве узлов. Если количество узлов дерева такое, что невозможно построить полное бинарное дерево, для получения бинарного дерева минимально возможной высоты необходимо заполнять все уровни дерева, кроме последнего, максимально возможным количеством узлов. Если оставшиеся узлы располагать на последнем уровне по порядку, начиная слева, то полученное таким образом бинарное дерево называют почти полным. На рис. 3.7, б изображено пости полное бинарное дерево.

Полные и почти полные бинарные деревья обладают еще одним интересным свойством — если их узлы нумеровать, начиная с единицы, сверху вниз и слева направо, то левому сыну всегда будет соответствовать код, в два раза больше кода его родителя, а правому сыну — код, на единицу больший, чем код код левого сына (рис.3.8). Номер корня всегда равен 1, его левый потомок получает номер 2, правый - номер 3. Левый потомок узла 2 получит номер 4, а правый - 5, левый потомок узла 3 получит номер 6, правый - 7 и т.д. Такая схема нумерации используется при представлении деревьев с помощью массивов. К этой теме мы еще вернемся.

Рис.3.8. Нумерация узлов полного или почти полного бинарного дерева

По такой схеме можно нумеровать и узлы бинарных деревьев, которые не являются почти полными, поскольку в этом случае гарантируется уникальность каждого номера, если в процессе работы к дереву добавляются новые листья. Используя такой способ нумерации, можно реализовать древовидную структуру на основе массива. Такая реализация будет приведена в главе 4.

После анализа основных свойств бинарных деревьев можно снова вернуться к упорядоченным деревьям и лесам и проанализировать соответствие между этими структурами и бинарным деревом.