3.2.3. Терминология деревьев

В предыдущих разделах уже были введены основные термины, касающиеся деревьев. Учитывая важность темы, рассмотрим этот вопрос подробно.

Стандартная терминология деревьев происходит от генеалогических деревьев. Каждый узел (элемент дерева) является родителем (parent) корней его поддеревьев, а сами корни называются братьями, а также детьми (child) или сыновьями своего родителя. Узлы, которые или являются детьми данного узла, или являются детьми его детей, называются потомками данного узла. И наоборот, родитель узла, а также родители родителей называются предками узла. Корень является общим предком всех узлов дерева. Сыновья узла иногда называются его непосредственными (истинными) потомками, а родитель — истинным предком.

Узел, не имеющий детей, называется листом или внешним узлом (leaf, external node). Остальные узлы являются внутренними (internal). Количество детей (непосредственных потомков) узла называется его степенью. Листья имеют степень ноль. Если максимальная степень узлов дерева больше двух, то такие деревья называют сильно ветвящимися.

Путем (path) из узла n1 в узел nk называется последовательность узлов n1. n2, ..., nk, где для всех i ( 1 i< k) узел ni, является родителем узла ni+1. Длиной пути называется число, на единицу меньшее числа узлов, составляющих этот путь (или равное количеству линий связи). Например, на рис. 3.2 путем из узла d в узел k будет являться последовательность d f k. Длина такого пути равна двум (две связи).

Основное свойство корневых деревьев — путь от корня до любого узла всегда существует и является единственным. Это свойство вытекает из того факта, что в иерархических структурах каждый узел всегда имеет только одного родителя (одну линию связи с родительским узлом), а значит, и единственный путь до корня дерева.

Высотой (height) узла дерева называется длина самого длинного пути из этого узла до какого-либо листа. Высота дерева совпадает с высотой корня.

Уровень узла (level) определяется как длина пути от корня до этого узла. Корень имеет уровень ноль. Все братья имеют один и тот же уровень, который на единицу больше уровня их отца. Например, на рис. 3.2 братья a, b и c имеют уровень 1, а сыновья узла с (братья e,f и g) имеют уровень 2. Высота дерева на рис.3.2 равна трем.

3.2.4. Упорядоченные деревья и леса. Связь с иерархическими списками

Упорядоченное (ordered) дерево — дерево, у которого относительный порядок сыновей (поддеревьев) имеет значение. Обычно сыновья упорядочиваются слева направо. Поэтому два дерева на рисунке 3.4. различны, так как порядок сыновей узла а различен.

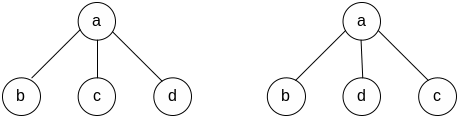
Рис. 3.4. Два различных упорядоченных дерева

Если порядок сыновей игнорируется, то такое дерево называется неупорядоченным. В большинстве алгоритмов используются упорядоченные деревья, очевидно, это объясняется тем, что расположение данных в памяти компьютера всегда имеет определенный порядок.

Если дерево является упорядоченным, то и каждый лес, являющийся частью этого дерева, также является упорядоченным. Упорядоченный лес можно рассматривать как линейный список деревьев, в котором можно четко выделить первое дерево (оно расположено слева от всех своих братьев), второе и т. д. Аналогично списку, в частном случае упорядоченный лес может не содержать ни одного дерева (быть пустым) или содержать одно единственное дерево.

Такое представление упорядоченного леса позволяет рассматривать упорядоченные леса (и деревья) как одну из разновидностей иерархических списков (вспомним определение иерархического списка). Однако иерархические списки считаются более универсальной структурой данных [8]:

несколько иерархических списков может пересекаться (т. е. иметь одинаковые подсписки);

иерархические списки могут даже быть рекурсивными (т. е. содержать ссылки на самих себя).

Такие возможности не противоречат определению иерархического списка, но не допустимы для деревьев исходя из их определения. Другими словами, для каждого дерева существует эквивалентная структура иерархического списка, однако есть иерархические списки, которые не соответствуют никакой древовидной структуре.

Примечание

Строго говоря, иерархические списки, которые пересекаются или содержат ссылку на самих себя, уже нельзя отнести к иерархическим структурам данных, правильнее назвать их многосвязными структурами. В фундаментальной работе [8] они рассматриваются именно как многосвязные структуры и называются Списками (с заглавной буквы). В реальных задачах такие нетривиальные случаи встречаются редко, поэтому термин «иерархические списки» — достаточно устоявшееся название подобных структур данных.

Далее рассмотрим еще один вид деревьев — бинарные.