2.4. Списки как абстрактные типы данных
2.4.1. Модель списка с выделенным текущим элементом
Будем считать, что состояние списка задается не только перечислением набора элементов, но и дополнительно указанием одного из них в качестве текущего элемента. Относительно этого элемента будет определяться семантика базовых операций. Заданием текущего элемента список разделяется на две части: от начала до текущего элемента (пройденная или прочитанная часть) и от текущего элемента (включая его) до конца списка (рис.2.9). К элементам пройденной части можно получить доступ, только начиная просмотр списка с начала. В непройденной части доступны все элементы поочередно, начиная с текущего элемента.
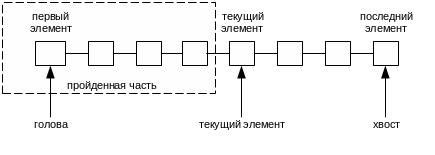
Рис.2.9. Модель списка с текущим элементом
Набор операций над списками существенно расширен по сравнению со стеками или очередями. В первую очередь это касается операций вставки и удаления — их теперь можно выполнять не только на концах, но в любой позиции списка, в зависимости от положения текущего элемента.
Операция вставки неформально определяется так — вставить элемент перед текущим, при этом текущим должен стать новый элемент. Особый случай вставки — новый элемент добавляется в конец списка.
При удалении текущего элемента следующий становится текущим. Нельзя удалять из пустого списка.
Одна из часто выполняемых операций над списками — получение значения текущего элемента. Можно выделить отдельную операцию изменения значения текущего элемента. Хотя ее можно представить как последовательность из двух операций (удаления с последующей вставкой), это будет неудобно в реализации.
Для любых списков требуются дополнительные операции создания пустого списка и проверки списка на наличие в нем хотя бы одного элемента.
Поскольку все базовые операции определяются относительно текущего элемента, обязательно должна быть обеспечена возможность изменения текущего элемента, иными словами, механизм передвижения по списку. Различные виды списков отличаются друг от друга именно по возможности передвижения по списку. Определим соответствющие абстрактные типы данных.
2.4.2. Однонаправленный список (список л1)
В однонаправленном списке двигаться от элемента к элементу можно только в одном направлении. Для многих приложений этого достаточно, допустим для выполнения таких действий над списками как вычисление суммы элементов, вычисление максимального элемента, изменение значений элементов и т. д.
Для передвижения по однонаправленному списку достаточно определить такие операции:
сделать текущим первый элемент (встать в начало списка);
сделать текущим следующий элемент (продвинуться вперед на один элемент):
проверить, не достигнут ли конец списка при переходе от текущего элемента к следующему, что может случиться, если текущим был последний элемент.
2.4.3. Двунаправленный список (список л2)
В списках Л2 базовые операции также определяются относительно текущего элемента (см. рис. 2.9), поэтому основной набор операций совпадает со списками Л1. Дополнительная возможность состоит в обходе списка не только в прямом, но и обратном направлении. Такая возможность требуется, например, при реализации просмотра или редактирования текстовых файлов с использованием списков и многих других алгоритмах.
Для того, чтобы сделать возможным движение по списку в двух направлениях, необходимо добавить к тем операциям, которые определены для однонаправленного списка, еще три дополнительных операции:
сделать текущим последний элемент (встать в конец списка);
сделать текущим предыдущий элемент (продвинуться назад на один элемент):
проверить состояние начала списка при переходе к предыдущему элементу, что может случиться, если текущим был первый элемент.
Формальную спецификацию списков Л1 и Л2 можно выполнить самостоятельно по аналогии со стеками и очередями. В следующем разделе, посвященном реализации списков, формальная спецификация будет выполнена средствами языка программирования.