2.3.2. Ссылочная реализация очереди в динамической памяти

Для реализации очереди, как и стека, достаточно иметь в каждом элементе по одному указателю на следующий элемент, как показано на рис.2.5. Но поскольку вставка и удаление выполняются на разных концах, то для эффективной реализации нужно хранить два дополнительных указателя — на хвост и голову очереди (как и в случае непрерывной реализации на массиве).

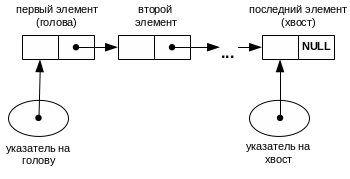
Рис.2.5. Представление очереди при помощи связного списка

Выполнение операций добавления и удаления элементов показано на рис. 2.6. и 2.7.

При добавлении элемента в хвост очереди достаточно:

• захватить под него память, заполнить информационную часть данными, указателю присвоить пустое значение;

• изменить указующую часть элемента, бывшего последним;

• присвоить указателю на хвост адрес добавленного элемента — он теперь будет хвостом очереди(рис.2.6)

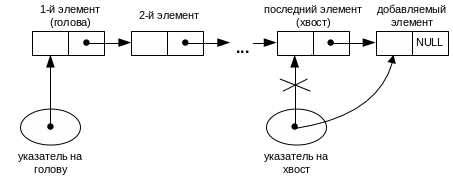
Рис.2.6. Добавление элемента в очередь

Удаление из головы очереди также выполняется просто — достаточно изменить указатель на голову и освободить память, которую занимал элемент, воспользовавшись буферной переменной (рис.2.7).

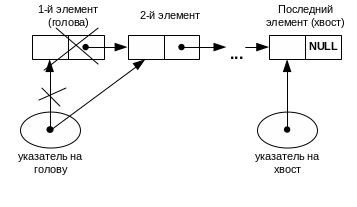
Рис.2.7.Удаление (извлечение) элемента из очереди

В листинге 2.4. приведена ссылочная реализация очереди в динамической памяти.

Листинг 2.4. Ссылочная реализация структуры queue на основе указателей

#include <stdlib.h>

#include <iostream.h>

typedef int type_of_data; // тип элементов (может быть любым)

struct item //структура каждого элемента очереди

{ type_of_data data; // данные

item *next; // указатель на следующий элемент

};

struct queue // описание структуры очереди

{ item *head,*tail; // указатели на хвост и голову

queue () { head=NULL; } //конструктор, создает пустую очередь

void enqueue(type_of_data x); //добавление элемента в хвост очереди

type_of_data dequeue(); // извлечение элемента из головы очереди

bool isnull() { return head==NULL; }//проверка на пустоту

void makenull(); // очистка очереди

};

void queue::enqueue (type_of_data x)

{ if (isnull()) //добавление первого элемента в пустую очередь

{ head=new item; head->data=x; head->next=NULL; tail=head;

}

else // добавление в непустую очередь

{ item *i=new item; i->data=x; i->next=NULL; tail->next=i; tail=i;

}

}

type_of_data queue::dequeue ()

{ if (isnull()) { cerr << "Очередь пуста\n"; exit(1); }

type_of_data x=head->data; item *i=head->next; // запомнили данные и указатель

delete head; head=i; // удалили голову и переставили указатель

return x; // возвратили данные

}

void queue::makenull()

{ while (!isnull()) dequeue(); // удаляем элементы по порядку

}

2.3.3. Ссылочная реализация очереди с помощью циклического списка

Использование циклического связного списка позволяет сэкономить на одном дополнительном указателе, и хранить только указатель на хвост очереди, поскольку указатель на голову уже содержится в указующей части хвоста очереди (рис.2.8).

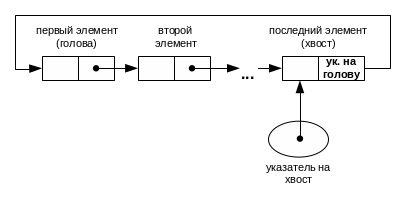
Рис.2.8. Реализация очереди на основе циклического списка

В целом реализация мало отличается от реализации с помощью двух указателей, необходимо только аккуратно отследить момент, когда очередь становится пустой и присвоить указателю на хвост нулевое значение. Если в очереди только один элемент, то указатель на хвост указывает на него, а он указывает сам на себя.