96. 8. Класифікація функцій

Розглянемо деякі класи функцій, що найбільш часто зустрічаються.

1. Многочлени або цілі раціональні функції.

Многочленом називається функція виду:

, (2.3)

де – сталі коефіцієнти многочлена, . Старший степінь змінної , називається степенем многочлена. Якщо , то степінь многочлена (2.3) дорівнює . Область визначення многочлена – усі дійсні значення змінної .

При маємо многочлен нульового степеня , де – число. Графік такої функції – пряма паралельна вісі

При маємо многочлен першого степеня , його називають лінійною функцією. Графіком такого многочлена є пряма.

При маємо многочлен другого степеня , таку функцію називають квадратичною функцією. Графіком квадратичної функції є парабола з вертикальною віссю симетрії.

2. Дробово-раціональні функції.

Дробово-раціональною функцією відносно називається функція, яку можна представити у вигляді відношення двох многочленів, тобто у вигляді:

, (2.4)

де – сталі.

Функція (2.4) визначена для всіх значень , крім тих, для яких знаменник дорівнює нулю. Прикладами дробово-раціональних функцій є функції , та ін.

Функція називається дробово-лінійною функцією від . Така функція визначена для всіх x, крім , графіком її є гіпербола.

3. Алгебраїчні функції.

Алгебраїчною називають функцію, одержану з аргументу і дійсних чисел за допомогою алгебраїчних операцій (додавання, віднімання, множення, ділення, піднесення до степеня і добування кореня). З означення випливає, що ціла раціональна і дробово-раціональна функція є алгебраїчними.

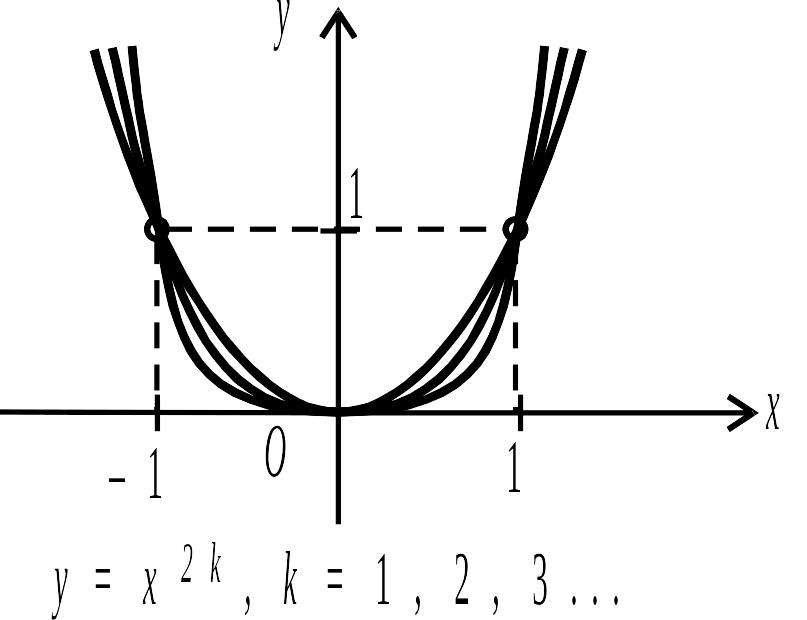
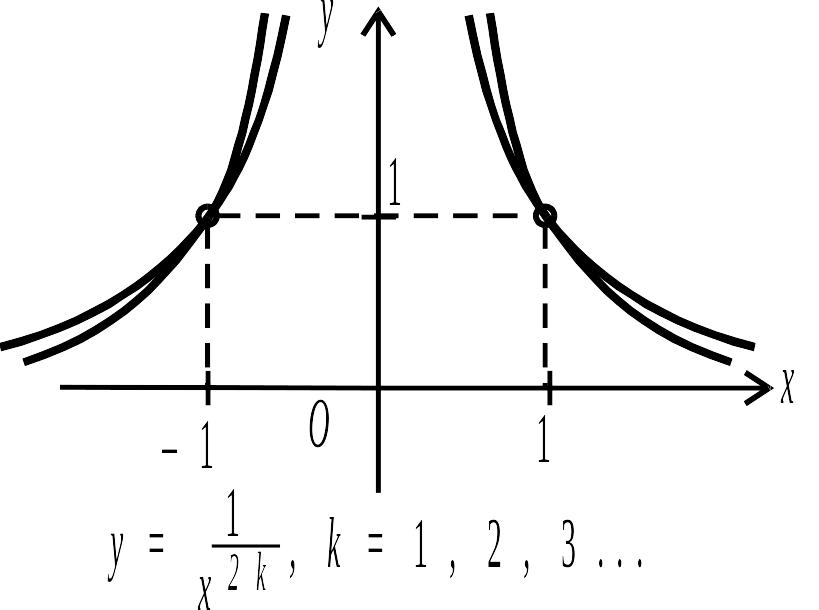
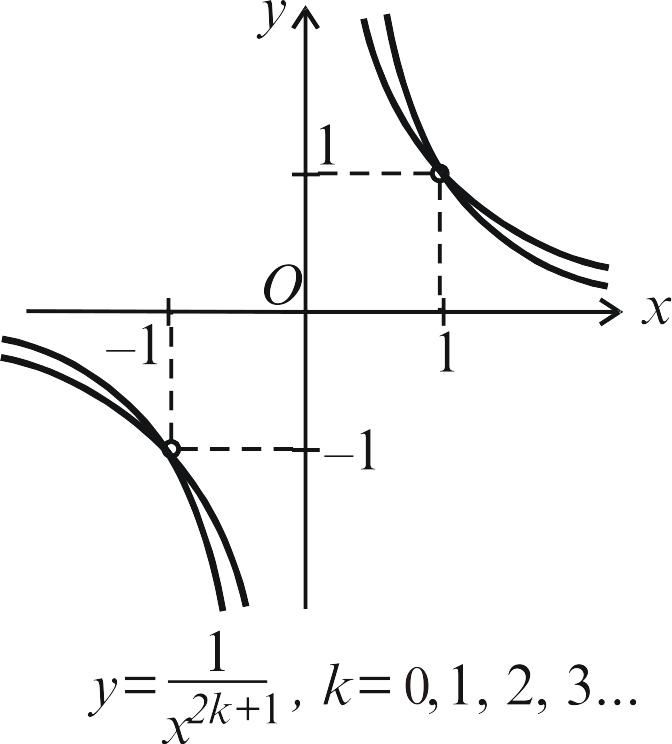
Алгебраїчні функції, що не є раціональними, називаються ірраціональними, наприклад, , і т.д. Окремим випадком алгебраїчної функції є степенева функція , де – раціональне число ( , ). Графіки деяких степеневих функцій показані на рис. 2.3–2.6.

Рис. 2.3.	Рис. 2.4.

Рис. 2.5.	Рис. 2.6.

4. Трансцендентні функції.

Трансцендентними функціями називаються усі функції, що не є алгебраїчними. До них належать показникові, логарифмічні, тригонометричні, обернені тригонометричні функції та ін.

Показниковою називається функція виду , де , . Функція визначена для всіх значень аргументу .

Графіки показникових функцій для випадку і наведено на рис. 2.7 а, б.

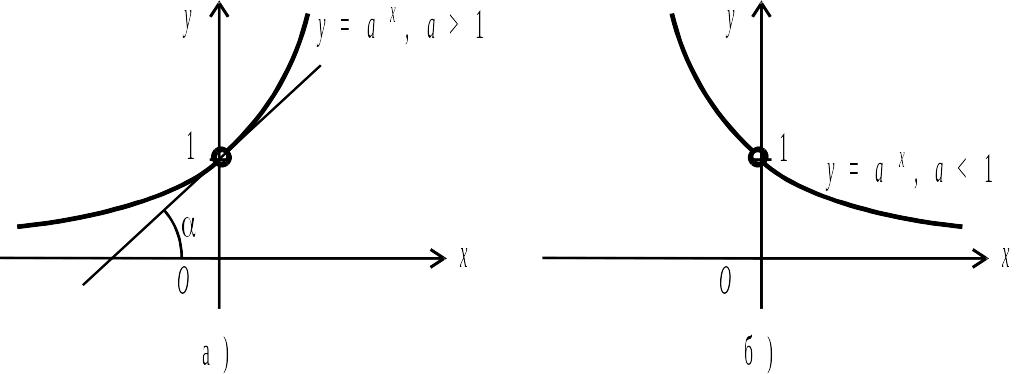
Рис. 2.7.

Те значення a, при якому кут  між віссю Ox і дотичною до кривої в точці її перетину з віссю Oy дорівнює .

Логарифмічна функція , де , визначається як функція, обернена до показникової .

Як і показникова функція, найбільш прості властивості має логарифмічна функція з основою , для якої введено символ .

Логарифми чисел з основою називають натуральними. Графіки логарифмічних функцій для випадку і наведено на рис. 2.8 а, б.

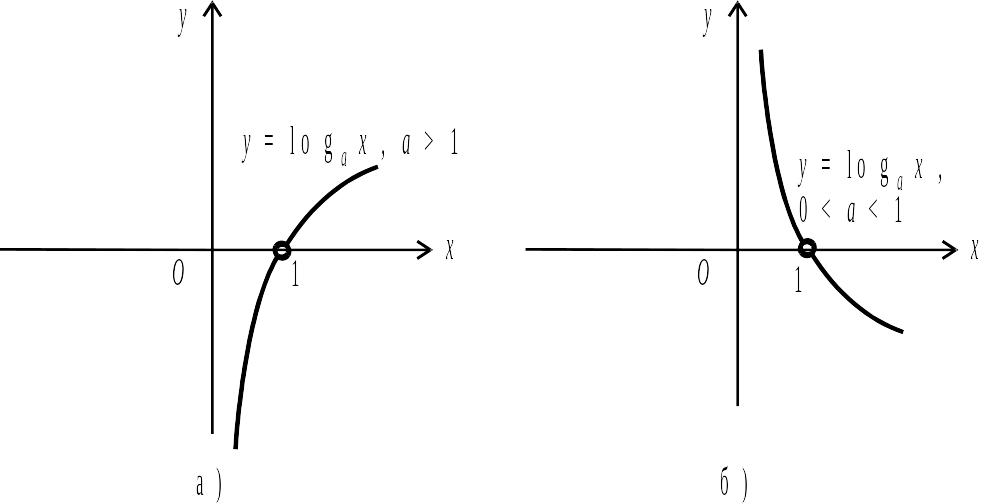
Рис. 2.8.

Тригонометричні функції , , , . Тут значенням аргументу є число, що є радіанною мірою деякого кута.

Функції і мають областю визначення всі значення змінної . Множиною значень цих функцій є відрізок . Графіки функцій і зображено на рис. 2.9 і 2.10.

Функція визначена для всіх значень , крім . Множина значень функції . Графік цієї функції наведено на рис. 2.11.

Функція визначена для всіх значень , крім , де . Множина значень функції: . Графік функції наведено на рис. 2.12.

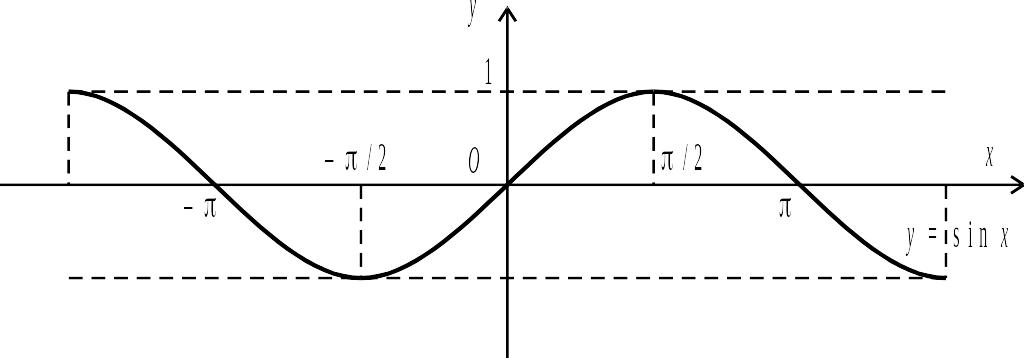
Рис. 2.9.

Рис. 2.10.

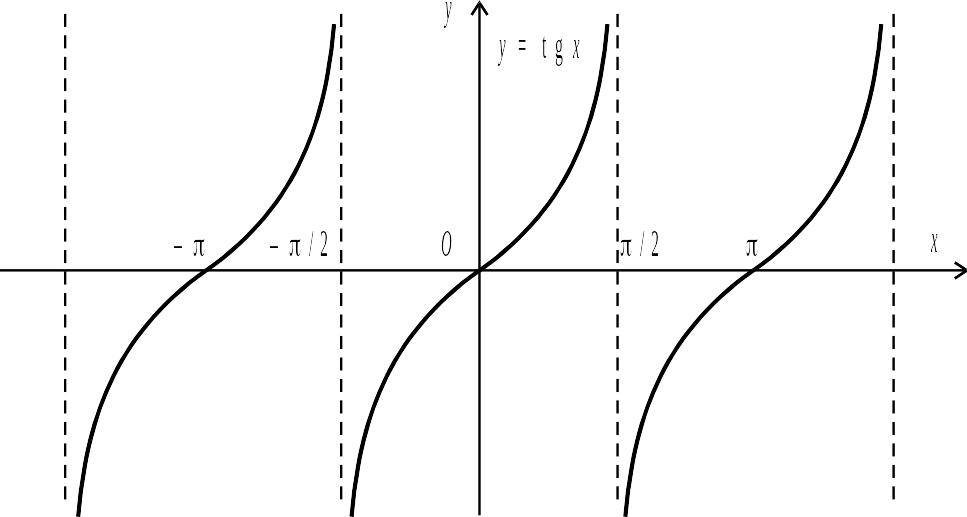
Рис. 2.11.

Рис. 2.12.

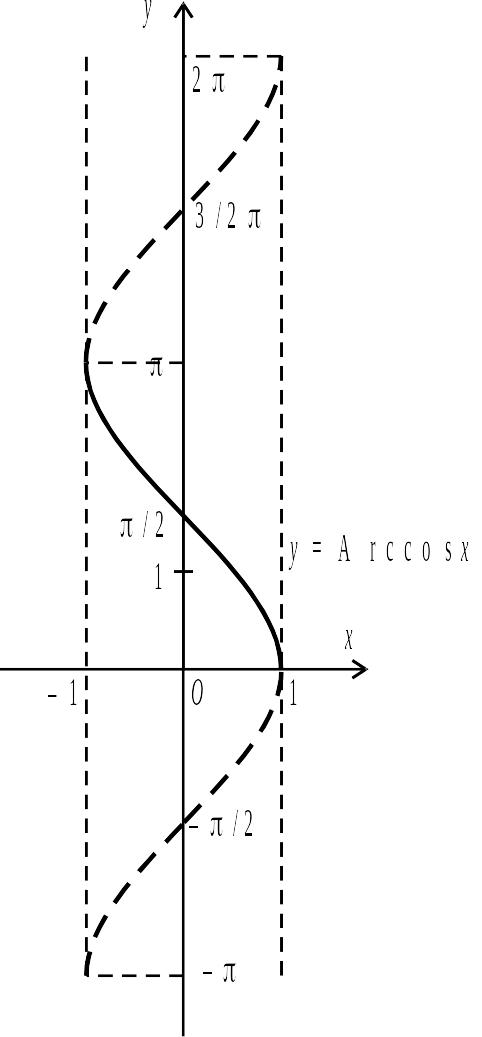
Оберненими тригонометричними функціями є функції , , , .

Функція – це дуга, розташована в межах , синус якої дорівнює : . Функція визначена на відрізку [–1;1].

Якщо відомі всі значення , синус яких дорівнює , одержимо багатозначну функцію, яку будемо позначати . Графіком цієї функції є синусоїда, віднесена до вісі . На підставі властивостей дуг, що мають однаковий синус, випливає формула:

.

Аналогічно функція – це дуга, розташована в межах , косинус якої дорівнює : .

Функція визначена на відрізку [–1;1]. Якщо відомі всі значення y, косинус яких дорівнює , одержимо багатозначну функцію, яку будемо позначати . Графіком такої функції є синусоїда, віднесена до осі , зміщена на вниз.

На підставі властивостей дуг, що мають однаковий косинус, випливає формула:

.

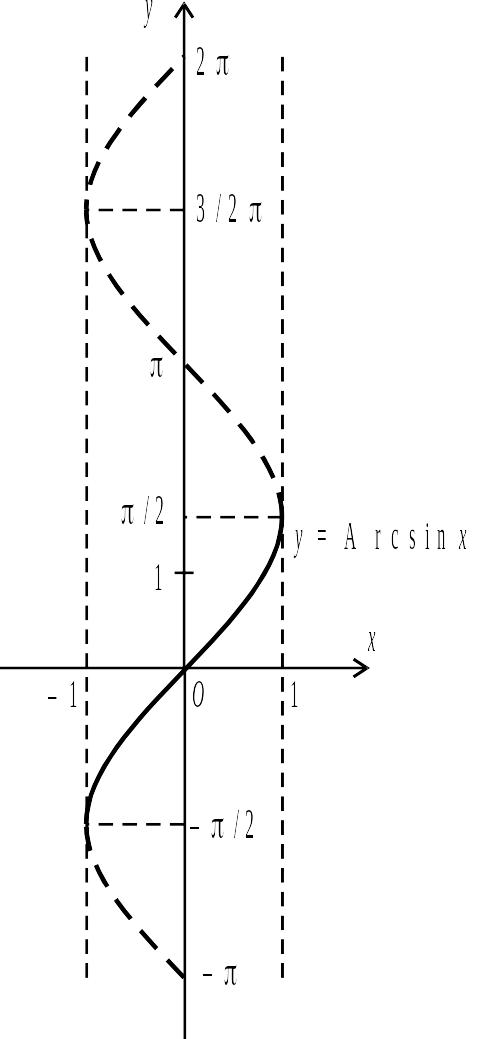
Графіки функцій , зображено на рис. 2.13 і 2.14 штриховою лінією. Графіками функцій , є частина дуги на відповідних рисунках, виділена суцільною лінією.

Рис. 2.13.	Рис. 2.14.

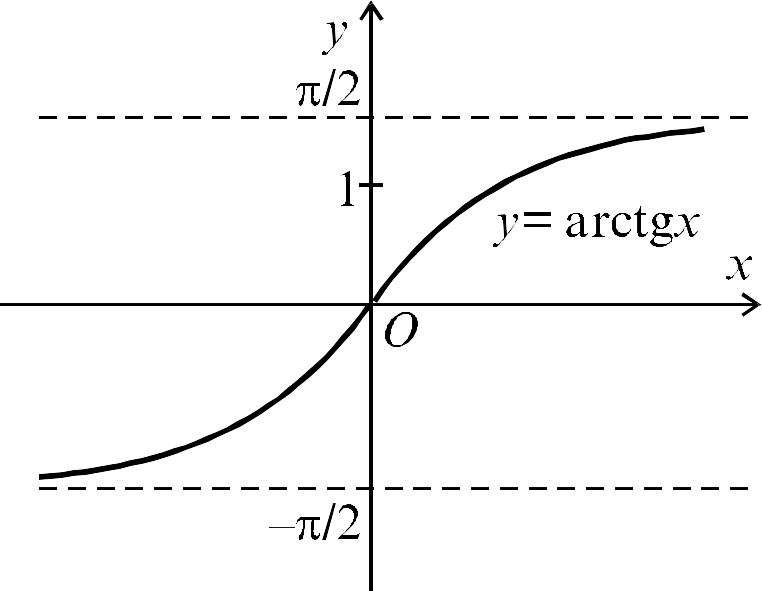
Функція – це дуга, розташована в межах , тангенс якої дорівнює : . Функція визначена на всій числовій прямій. Якщо вказати всі значення , тангенс яких дорівнює , одержимо багатозначну функцію , причому:

.

Графік функції зображено на рис. 2.15.

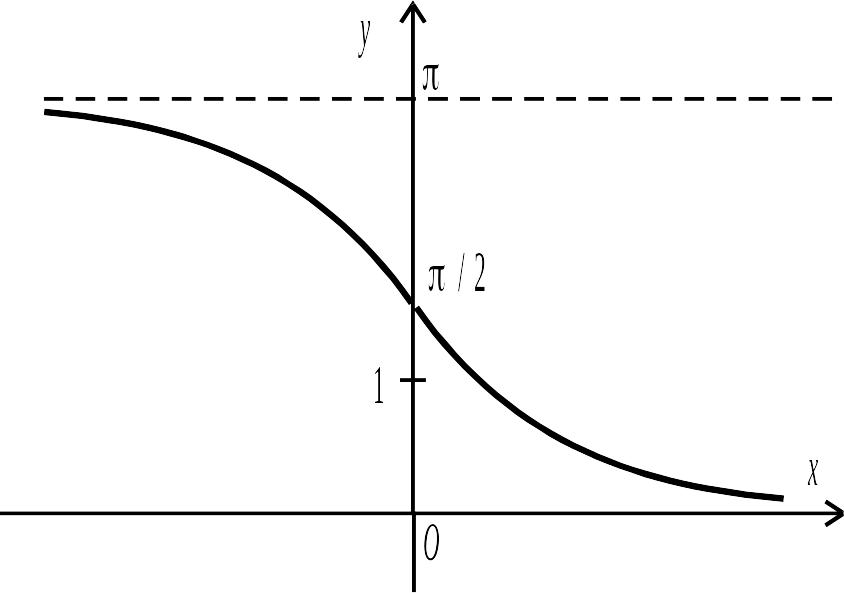
Функція – це дуга, розташована в межах , котангенс якої дорівнює : . Функція визначена на всій числовій прямій.

Якщо врахувати всі значення , котангенс яких дорівнює , одержимо багатозначну функцію , причому:

.

Графік функції зображений на рис. 2.16.

Рис. 2.15.	Рис. 2.16.

Будемо називати елементарними функціями степеневу, показникову, логарифмічну, тригонометричні і обернені тригонометричні.

Функції, одержані з елементарних за допомогою скінченного числа алгебраїчних дій і скінченного числа операцій обчислення функції від функції, будемо називати елементарними функціями.